
Конспект №14
Синтетическая Геометрия1
Def. Пусть дана некоторая окружность О и точка А снаружи (на той же плоскости).
Проведём из А секущие АВ1С1,
АВ2С2,... Как известно, величина
А В1АС1=АВ2АС2=...является
инвариантом при данных А и О. Назовём
её степенью точки А относительно О.
В1АС1=АВ2АС2=...является
инвариантом при данных А и О. Назовём
её степенью точки А относительно О.
П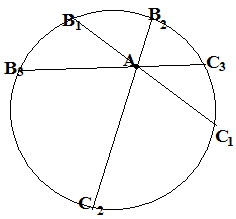 усть
О – центр этой окружности, а r
– её радиус, пусть АО=d.
Тогда степень точки А относительно О
А(О)=d2-r2
(почему?).
Если точка А лежит внутри
окружности, то опять-таки, АВ1АС1=АВ2АС2=...
Разница с первым случаем в том, что, если
раньше вектора АВ1 и АС1 были
направлены в одну сторону, то теперь –
в разные, и потому должны иметь разные
знаки. В прежних обозначениях вновь
получаем А(О)=d2-r2.
Заметим, что теперь эта величина
отрицательная. Естественно считать
степень точки, находящейся на окружности
нулевой.
усть
О – центр этой окружности, а r
– её радиус, пусть АО=d.
Тогда степень точки А относительно О
А(О)=d2-r2
(почему?).
Если точка А лежит внутри
окружности, то опять-таки, АВ1АС1=АВ2АС2=...
Разница с первым случаем в том, что, если
раньше вектора АВ1 и АС1 были
направлены в одну сторону, то теперь –
в разные, и потому должны иметь разные
знаки. В прежних обозначениях вновь
получаем А(О)=d2-r2.
Заметим, что теперь эта величина
отрицательная. Естественно считать
степень точки, находящейся на окружности
нулевой.
У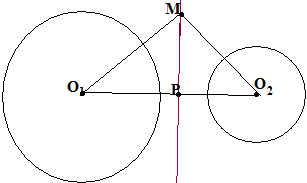 пражнение
№1.
Пусть нам даны две окружности
с радиусами r1 и r2
соответственно и расстоянием между
центрами равным 2f. Поставим
задачу: найти ГМТ, степени которых
относительно данных окружностей равны.
Докажите, что таким ГМТ всегда будет
прямая линия, перпендикулярная линии
центров.
пражнение
№1.
Пусть нам даны две окружности
с радиусами r1 и r2
соответственно и расстоянием между
центрами равным 2f. Поставим
задачу: найти ГМТ, степени которых
относительно данных окружностей равны.
Докажите, что таким ГМТ всегда будет
прямая линия, перпендикулярная линии
центров.
Напишите систему уравнений из которых (единственным) образом определяется точка Р на линии центров. Пусть окружности расположены, как показано на рисунке – каждая вне другой. Что можно сказать о местоположении Р, если, например, r1>r2 – будет ли она ближе к О1 или к О2? К какой из двух окружностей будет она ближе? Def. Этот перпендикуляр называется радикальной осью двух окружностей.
Упражнение №2.
Как проходит радикальная ось для двух окружностей, находящихся одна в другой?
Ч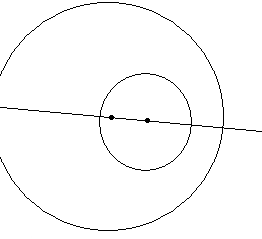 то
происходит при сближении их центров?
то
происходит при сближении их центров?
Как проходит радикальная ось двух пересекающихся окружностей?
Упражнение №3.
Д
 окажите,
что радикальная ось для двух окружностей,
расположенных одна вне другой, являются
также ГМТ, из которых длины касательных
к обеим окружностям равны. Докажите
также, что общая касательная к двум этим
окружностям делится радикальной осью
пополам.
Упражнение
№4.
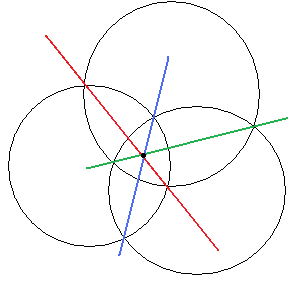
Докажите» что радикальные
оси каждой пары данных трёх кругов
сходятся в одной точке, называемой
радикальным центром трёх
окружностей. Иными словами, эти прямые
конкуррентны. В частности, прямые,
содержащие общие хорды трёх попарно
пересекающихся кругов, пересекаются в
одной точке.
Упражнение
№5*. (Теорема Брианшона)
Пусть
описанный шестиугольник ABCDEF
каксается окружности в точках MNPQRS.
Если перенумеровать вершины и стороны
шестиугольника против (или по) часовой
стрелке 1, 2, 3, 4, 5, 6, то противоположными
считаются вершины (стороны) с номерами,
сравнимыми по модулю 3: 1 и 4, 2 и 5, 3 и 6.
Соответственно, главными диагоналями
шестиугольника называются диагонали,
соединящие противоположные вершины.
Их, стало быть, три. Так вот, теорема
утверждает, что все они пересекаются
в одной точке (называемой точкой
Брианшона).
окажите,
что радикальная ось для двух окружностей,
расположенных одна вне другой, являются
также ГМТ, из которых длины касательных
к обеим окружностям равны. Докажите
также, что общая касательная к двум этим
окружностям делится радикальной осью
пополам.
Упражнение
№4.
Докажите» что радикальные
оси каждой пары данных трёх кругов
сходятся в одной точке, называемой
радикальным центром трёх
окружностей. Иными словами, эти прямые
конкуррентны. В частности, прямые,
содержащие общие хорды трёх попарно
пересекающихся кругов, пересекаются в
одной точке.
Упражнение
№5*. (Теорема Брианшона)
Пусть
описанный шестиугольник ABCDEF
каксается окружности в точках MNPQRS.
Если перенумеровать вершины и стороны
шестиугольника против (или по) часовой
стрелке 1, 2, 3, 4, 5, 6, то противоположными
считаются вершины (стороны) с номерами,
сравнимыми по модулю 3: 1 и 4, 2 и 5, 3 и 6.
Соответственно, главными диагоналями
шестиугольника называются диагонали,
соединящие противоположные вершины.
Их, стало быть, три. Так вот, теорема
утверждает, что все они пересекаются
в одной точке (называемой точкой
Брианшона).
П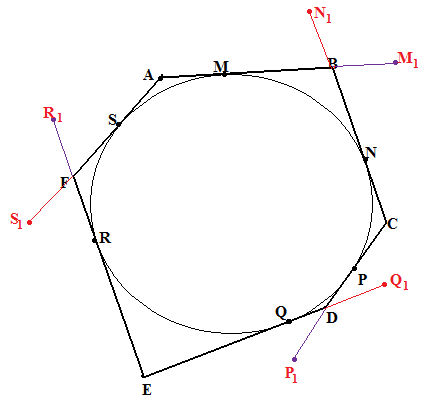 оскольку
давать вам доказывать такую теорему
полностью самостоятельно было бы
нечестно, подскажу дополнительное
построение. Отложите отрезки
РР1=RR1=MM1=NN1=SS1=QQ1
как указано на рисунке. Докажите, что
существуют три окружности: О1,
касающаяся пар прямых AF
и CD в точках S1
и P1, О2,
касающаяся пар прямых BC
и EF в точках R1
и N1 и О3,
касающаяся пар прямых AB
и ED в точках Q1
и M1.
оскольку
давать вам доказывать такую теорему
полностью самостоятельно было бы
нечестно, подскажу дополнительное
построение. Отложите отрезки
РР1=RR1=MM1=NN1=SS1=QQ1
как указано на рисунке. Докажите, что
существуют три окружности: О1,
касающаяся пар прямых AF
и CD в точках S1
и P1, О2,
касающаяся пар прямых BC
и EF в точках R1
и N1 и О3,
касающаяся пар прямых AB
и ED в точках Q1
и M1.
Теперь заметьте, что, например, А(О1)=А(О3) и D(O1)=D(O3). Завершите рассуждение.
Если две достаточно «гладкие»2 кривые пересекаются, то угол между касательными к ним в их общей точке пересечения называется углом между этими кривыми в этой их общей точке. Если этот угол - прямой, то кривые называются ортогональными в данной точке.
Упражнение №6.
Пусть круги, соответствующие окружностям О1 и О2 не пересекаются. Докажите, что любая точка их радикальной оси служит центром некоторой (единственной) окружности, ортогональной обеим окружностям О1 и О2. Она же (радикальной ось) является и ГМ таких точек (центров окружностей, ортогональных обеим данным окружностям).
Упражнение №7.
П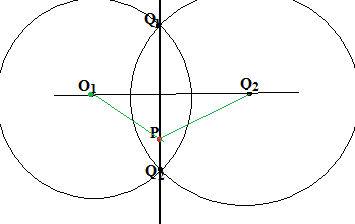 усть
теперь О1 и О2 пересекаются
в точках Q1 и Q2.
усть
теперь О1 и О2 пересекаются
в точках Q1 и Q2.
Т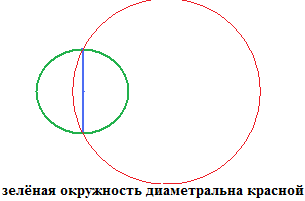 огда
любая точка радикальной оси, за исключением
точек отрезка Q1Q2
служит центром окружности, ортогональной
обеим окружностям О1 и О2.
Возьмём произвольную точку РQ1Q2.
Докажите, что существует (единственная)
окружность О3 с центром Р, такая,
что её точки пересечения с каждой из
двух окружностей О1 и О2
явдяются антиподальными (т.е., концами
её диаметров). Об окружностях с таким
свойством говорят, что они диаметральны
(по отношению к окружностям О1 и
О2).
огда
любая точка радикальной оси, за исключением
точек отрезка Q1Q2
служит центром окружности, ортогональной
обеим окружностям О1 и О2.
Возьмём произвольную точку РQ1Q2.
Докажите, что существует (единственная)
окружность О3 с центром Р, такая,
что её точки пересечения с каждой из
двух окружностей О1 и О2
явдяются антиподальными (т.е., концами
её диаметров). Об окружностях с таким
свойством говорят, что они диаметральны
(по отношению к окружностям О1 и
О2).
Пусть теперь окружности О1 и О2 пересекаются в точках Q1 и Q2. Центры всех окружностей, проходящих через точки Q1 и Q2, расположены на прямой О1О2. Для каждой пары таких окружностей радикальной осью служит прямая Q1Q2. Говорят, что все эти окружности образуют пучок окружностей, а прямая является радикальной осью этого пучка. Обозначим буквой M точку пересечения этих двух прямых. Построим окружность с центром в М и радиусом МQ1=М Q2. Очевидно, что она диаметральна всем окружностям данного пучка. Более того, сам пучок можно определить как множество всех окружностей с центрами на прямой, проходящей через точку М - центр данной окружности, для которых эта окружность диаметральна.
П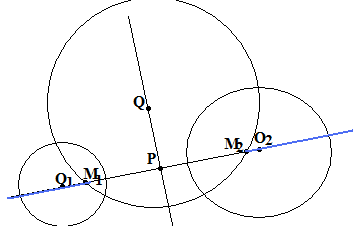 усть
теперь окружности О1 и О2 не
пересекаются и пусть Q1Q2
- их радикальная ось. Возьмём на ней
произвольную точку QQ1Q2.
Построим окружность q,
ортогональную обеим окружностям О1
и О2, как в упражнении 6. Пусть
она пересекает прямую О1О2
в точках М1 и М2.
усть
теперь окружности О1 и О2 не
пересекаются и пусть Q1Q2
- их радикальная ось. Возьмём на ней
произвольную точку QQ1Q2.
Построим окружность q,
ортогональную обеим окружностям О1
и О2, как в упражнении 6. Пусть
она пересекает прямую О1О2
в точках М1 и М2.
Упражнение №8.
Докажите, что для каждой пары точек прямой О1О2, кроме точек отрезка М1М2, полученная окружность q будет ортогональна некоторым окружностям с центрами в этих точках (эти окружности для каждой пары точек строятся единственным образом).
Множество этих окружностей (радикальной осью для которых по-прежнему служит прямая Q1Q2) также называется пучком, хотя их центры уже не составляют целую прямую. Сами точки М1 и М2 также можно включить в этот пучок, считая их центрами окружностей нулевого радиуса (вырожденных в точку окружностей).
Упражнение №9.
Докажите, что окружность Р с центром в точке Р=Q1Q2О1О2 и радиусом РМ1=РМ2 ортогональна всем окружностям этого пучка. Поэтому и сам пучок может быть определён и как пучок окружностей, ортогональных данной окружности Р и имеющих центры на определённой прямой, проходящей через его центр.
Пучок окружностей, имеющих две общие точки, называется эллиптическим, не имеющих общих точек – гиперболическим, а имеющих одну общую точку – параболическим.
Рассмотрим пучок окружностей О, О1, О2,...и вычислим тепень точки МО относительно окружности О1. Пусть секущая из точки М пересекает окружность О во второй раз в точке N, а окружность О1 в точках А и В, встречая на своём пути радикальную ось в точке С.
О пустим
из центров О и О1 перпендикуляры
ОЕ и О1F на прямую
MNCAB. Опустим из М перпендикуляр
MG на радикальную ось и
проведём О1Н||MNCAB.
пустим
из центров О и О1 перпендикуляры
ОЕ и О1F на прямую
MNCAB. Опустим из М перпендикуляр
MG на радикальную ось и
проведём О1Н||MNCAB.
Упражнение №10.
Учтя, что МС+NC=2CE и CA+CB=2CF, выведите, что М(О1)=2МСF, а из подобия треугольников ОО1Н и МСG получите, что М(О1)=2 ОО1МG. Таким образом, степень точки, лежащей на одной окружности пучка относительно другой окружности пучка равна удвоенному произведению расстояния между центрами этих окружностей на расстояние от этой точки до их радикальной оси.
Если взять третью окружность О2 того же пучка, то получим М(О):М(О2)=ОО1:ОО2. Если считать окружности О1 и О2 фиксированными, то множество окружностей их пучка может быть охарактеризовано как ГМТ, степени которых относительно этих окружностей находятся в постоянном отношении.
Упражнение №11*.
Построить окружность, касающуюся данной
окружности O и проходящую
через две заданные точки A
и B. (Hint:
consider
an
arbitrary
auxiliary
circumference
O2,
crossing
A
and
B.
Consider
the
radical
center
of
O,
О2 and
circumference
sought)

Рассмотрите оба случая: когда точки расположены вне и внутри окружности О. Рассматривая прямую, как окружность бесконечного радиуса, используйте решение этой задачи для решения уже знакомой вам задачи о построении окружности, проходящей через две заданные точки, расположенных в одной полуплоскости от заданной прямой, и касающейся этой прямой.
Сделаем небольшое отступление, касающееся деления отрезка в данном отношении.
Пусть у нас есть отрезок АВ. Будем, с одной стороны, рассматривать отрезки направленными, т.е., считать их векторами, с другой стороны понимать под длиной вектора длину отрезка, соответствующего этому вектору. Поскольку сравнивать мы будем только пары векторов, лежащих на одной прямой, то они будут одного знака (вне зависимости от ориентации этой прямой), если смотрят в одну сторону, и разных знаков, если направлены в разные стороны.
Упражнение №12.
![]()
Докажите, что q0 !MAB| AM:MB=q !NAB| AN:NB=-q.
Чем отличаются положения точки N в случаях q<1 и q>1? Что можно сказать о случае q=1? Какому положению М это соответствует?
П
 усть
нам уже дана на отрезке АВ точка М,
делящая его в отношении q.
Как наиболее быстро (за наименьшее
количество действий – проведении
прямых и окружностей) с помощью циркуля
и линейки найти на прямой АВ точку
N?
(Hint:
look
at
the
picture)
усть
нам уже дана на отрезке АВ точка М,
делящая его в отношении q.
Как наиболее быстро (за наименьшее
количество действий – проведении
прямых и окружностей) с помощью циркуля
и линейки найти на прямой АВ точку
N?
(Hint:
look
at
the
picture)
Говорят, что точка М делит отрезок АВ внутренним образом, а точка N – внешним.
Точки М и N называются гармонически сопряжёнными относительно точек А и В. Говорят также, что точки М и N делят гармонически отрезок АВ.
Упражнение №13. Докажите, что и обратно, точки А и В делят гармонически отрезок МN.
Про четыре точки [A,M,B,N] взятых именно в таком порядке (порядок важен) говорят, что они находятся в гармоническом отношении или являются гармонической четвёркой точек, если двойное отношение (АМ:МВ):(BN:NA)=-1.
Гомотетию с положительным коэффициентом мы будем называть прямой, а с отрицательным – обратной гомотетией. Нам придётся различать оба этих случая.
Пусть два круга О1 и О2 с радиусами r1 и r2 не пересекаются.
У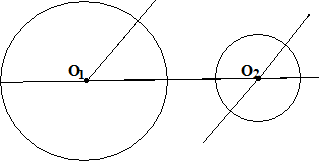 пражнение
№14.
Найдите для них центры прямой
и обратной гомотетий (при которых один
круг получается преобразованием
плоскости из другого). Чертёж вам послужит
подсказкой.
пражнение
№14.
Найдите для них центры прямой
и обратной гомотетий (при которых один
круг получается преобразованием
плоскости из другого). Чертёж вам послужит
подсказкой.
Центр прямой гомотетии называется в этом случае внешним центром подобия. Её коэффициент равен отношению радиусов. В этом же отношении центр гомотетии делит расстояние между центрами окружностей внешним образом Докажите, что через него проходят обе общие внешние касательные к окружностям.
Упражнение №15.
Докажите, что центр обратной гомотетии (называемый внутренним центром подобия) делит отрезок О1О2 внутренним образом в отношении r1: r2 и через него проходят обе общие внутренние касательные к обеим окружностям.
Таким образом, центры подобия двух окружностей гармонически делят расстояние между их центрами.
Упражнение №16.
Рассмотрите случай пересечения, касания окружностей внутренним и внешним образом и содержания одного круга целиком внутри другого.
Пусть теперь у нас имеются три окружности O1(r1), O2(r2) и O3(r3).
Мы исключительно ради большей наглядности изображаем лишь случай непересечения соответствующих кругов, хотя нигде этим пользоваться не будем.
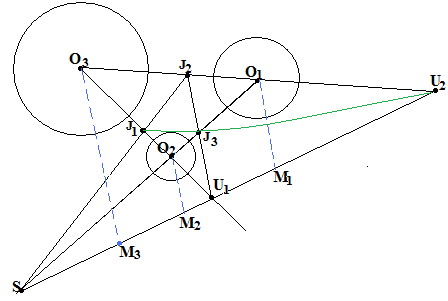 Пусть
U1 и U2
обозначают внешние центры подобия для
пар (O2,O3)
и (O3,O1)
соответственно. Проведём прямые
О1М1||O2M2||O3M3
до пересечения с прямой U1U2.
Пусть
U1 и U2
обозначают внешние центры подобия для
пар (O2,O3)
и (O3,O1)
соответственно. Проведём прямые
О1М1||O2M2||O3M3
до пересечения с прямой U1U2.
Упражнение №17.
Обоснуйте равенства
![]() и
и
![]() и получите равенство
и получите равенство
![]() .
.
Пусть S=U1U2О1О2.
Упражнение №18.
Докажите, что O2S:SO1=-r2:r1 и, таким образом, точка S является внешним центром подобия окружностей О1 и О2.
Итак S=U3, то есть внешние центры подобия трёх окружностей, взятых попарно, расположены на одной прямой.
Действуя по образцу и подобию, докажите, что
Упражнение №19.
Каждая пара внутренних центров подобия расположена на одной прямой с одним из внешних центров подобия.
Т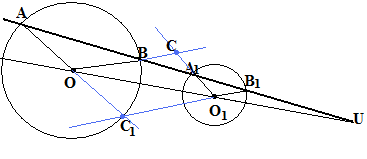 аким
образом, шесть центров подобия трёх
кругов расположены тройками на четырёх
прямых.
аким
образом, шесть центров подобия трёх
кругов расположены тройками на четырёх
прямых.
Построим два круга – О и О1 и пусть U – их внешний центр подобия.
Проведём из него секущую, пересекающую окружность О в точках А и В, а окружность О1 – в точках А1 и В1.
Тогда ОА||OA1 и OB||OB1.
Назовём точки А и А1, В и В1, являющиеся концами параллельных радиусов, сответствующими точками секущей, а пары (В, А1) и (А,В1) - несответствующими точками секущей.
Прведём прямые ОА и ОВ, О1А1 и О1В1 до их пересечения в точках С и С1. Получим параллелограмм ОСО1А1.
Упражнение №20.
Докажите, что треугольники ВСА1 и АВ1С1 – равнобедренные и точка С является центром окружности, касающейся окружностей О и О1 в точках В и А1 внешним образом, а точка С1 - центром окружности, касающейся окружностей О и О1 в точках В и А1 внутренним образом.
Докажите и обратное утверждение.
Упражнение №21.
П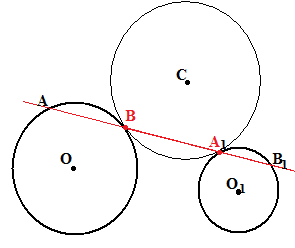 усть
окружность С касается окружностей О и
О1 в точках В и А1 внешним
образом.
Тогда прямая ВА1
проходит через внешний центр подобия
окружностей О и О1.
Пусть теперь
J – внутренний центр
подобия окружностей О и О1. Пусть
секущая, проходящая через J
пересекает эти окружности в точках А,
В, А1 и В1, причём А и А1,
В и В1 – соответствующие точки, а
А и В1, А1 и В – несоответствующие.
Проведём прямые ОА и ОВ, О1А1
и О1В1 до их пересечения в
точках С и С1. Получим параллелограмм
ОСО1А1.
усть
окружность С касается окружностей О и
О1 в точках В и А1 внешним
образом.
Тогда прямая ВА1
проходит через внешний центр подобия
окружностей О и О1.
Пусть теперь
J – внутренний центр
подобия окружностей О и О1. Пусть
секущая, проходящая через J
пересекает эти окружности в точках А,
В, А1 и В1, причём А и А1,
В и В1 – соответствующие точки, а
А и В1, А1 и В – несоответствующие.
Проведём прямые ОА и ОВ, О1А1
и О1В1 до их пересечения в
точках С и С1. Получим параллелограмм
ОСО1А1.
Упражнение №22.
Докажите, что треугольники В1СА и А1ВС1 – равнобедренные и точка С является центром окружности, касающейся окружностей О и О1 в точках В и А1 а точка С1 - центром окружности, касающейся окружностей О и О1 в точках В и А1, причём в обоих случаях – неодинаковым образом.
Обратно,
Упражнение №23.
Если третья окружность касается двух данных неодинаковым образом, то прямая, соединяющая точки касания, проходит через внутренний центр подобия данных окружностей.
Упражнение №24.
Произведение отрезков секущей от внешнего центра подобия до несоответствующих точек постоянно и равно произведению отрезков касательной, проведённой из этого центра подобия.
Произведение отрезков секущей от внутреннего центра подобия до несоответствующих точек постоянно и равно произведению отрезков касательной, проведённой из этого центра подобия.
Упражнение №25.
Если две окружности касаются двух данных окружностей одинаковым образом, то радикальная ось первой пары окружностей проходит через внешний центр подобия второй пары окружностей;
Если две окружности касаются двух данных окружностей неодинаковым образом, то радикальная ось первой пары окружностей проходит через внутренний центр подобия второй пары окружностей.
Пусть теперь две окружности, С1 и С2 касаются друг друга внутренним образом в точке А.
Впишем в них ещё две окружности О1 и О2, касающихся друг друга в точке В и окружностей С1 и С2, одну внутренним, а другую внешним образом. Точки касания окружности С1 с окружностями О1 и О2 обозначим через Е и F соответственно.
Упражнение №26.
Докажите, что точка пересечения U общей касательной к окружностям С1 и С2 в точке А и линии центров окружностей О1 и О2 является внешним центром подобия окружностей О1 и О2;
Т
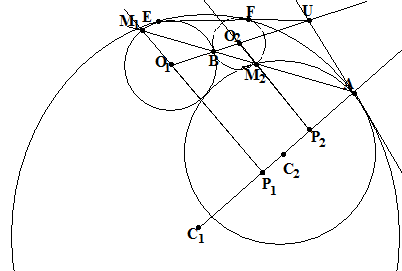 очки
U, E и F
инцидентны одной прямой, причём точки
E и F являются
несоответствующими точками этой
секущей;
очки
U, E и F
инцидентны одной прямой, причём точки
E и F являются
несоответствующими точками этой
секущей;UB=UA.
Проведём прямую АВ и прямые О1Р1С1С2 и О2Р2С1С2. Обозначим М1=О1Р1АВ и М2=О2Р2АВ.
Упражнение №27.
Точка М1 лежит на окружности О1, а точка М2 лежит на окружности М2.
Обозначим радиусы О1 и О2 за r1 и r2, а расстояния от центров О1 и О2 до линии центров С1 и С2 за р1 и р2.
Упражнение №28. (Теорема Паппуса)
Докажите, что
![]() .
.
Назовём отношение расстояния от центра окружности, вписанной в две касающихся друг друга внутренним образом окружности, до их линии центров к её радиусу коэффициентом этой окружности. Таким образом, разность коэффициентов двух касающихся друг друга вписанных окружностей равна (по модулю) 2. В частности, для последовательности окружностей, первая из которых имеет свой центр на линии центров С1 и С2, эта последовательность коэффициентов выглядит, как последовательность чётных чисел 0, 2, 4,...а для последовательности окружностей, первая из которых касается линии центров, эта последовательность коэффициентов выглядит, как последовательность нечётных чисел 1, 3, 5,...
Упражнение №29.
П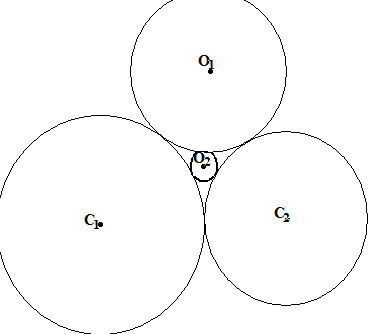 роверьте,
выполняется ли теорема Паппуса для
случая внешнего касания окружностей
С1 и С2.
роверьте,
выполняется ли теорема Паппуса для
случая внешнего касания окружностей
С1 и С2.
Если представлять себе прямую, как окружность бесконечно большого радиуса, то оба случая касания сводятся к окружности и её касательной. Как в этом случае формулируется теорема?
Упражнение №30.
П усть
окружность О пересекает ортогонально
окружности О1 и О2 в точках
А и D соответственно,
пересекая их ещё раз в точках В и С
соответственно. Пусть М= О1АО2D.
усть
окружность О пересекает ортогонально
окружности О1 и О2 в точках
А и D соответственно,
пересекая их ещё раз в точках В и С
соответственно. Пусть М= О1АО2D.
Докажите, что в точках В и С окружность О также пересекает окружности О1 и О2 ортогонально;
Докажите, что М является центром окружности, касающейся окружностей О1 и О2 в точках А и D
Докажите, что и другие пары точек А и С, В и D, В и С являются точками касания окружностей О1 и О2 некоторыми окружностями. Где расположены их центры?
Покажите, что точка пересечения прямых АD и ВС является внешним центром подобия окружностей О1 и О2, а точка пересечения прямых АС и ВD является их внутренним центром подобия.
Упражнение №31.* (Теорема Паскаля)
П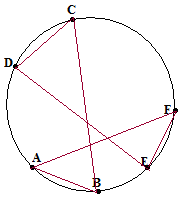 усть
на окружности О расположены 6 точек А,
В, С, D, E и
F, причём предположим, что
никакая пара противоположных точек (А
и D, B и E,
C и F) не
являются антиподальными, т.е., не явдляются
концами одного диаметра. Соединив их,
получим шестиугольник ABCDEF,
возможно невыпуклый и самопересекающийся,
как на рисунке.
усть
на окружности О расположены 6 точек А,
В, С, D, E и
F, причём предположим, что
никакая пара противоположных точек (А
и D, B и E,
C и F) не
являются антиподальными, т.е., не явдляются
концами одного диаметра. Соединив их,
получим шестиугольник ABCDEF,
возможно невыпуклый и самопересекающийся,
как на рисунке.
Для каждой пары противоположных точек (А и D, B и E, C и F) построим окружности, ортогональные окружности О.
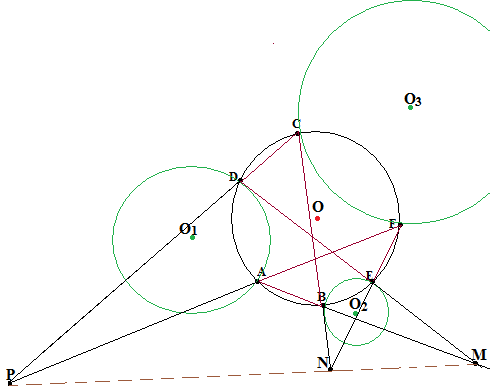
Докажите, что три прямые, содержащие три пары противоположных сторон шестиугольника, пересекаются в трёх точках, инцидентных одной прямой.
Упражнение №32.
Рассмотрите другой случай расположения точек, приводящий к конфигурации «два внутренних центра подобия и один внешний»
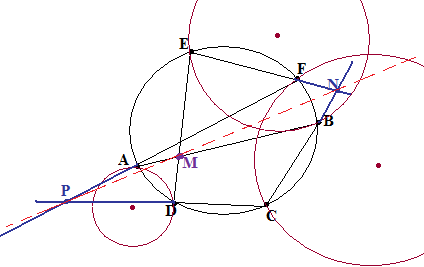
Как интерпретировать случаи, когда среди пар противоположных сторон имеются параллельные?
Какие точки следует считать центрами подобия окружности и прямой, если последнюю считать окружностью бесконечно большого радиуса?
Какие точки следует считать центрами подобия двух прямых, если последние считать окружностями бесконечно большого радиуса?
Разберите теперь случай, когда среди пар противоположных вершин шестиугольника имеются антиподальные.
Сравните теоремы Паскаля и Брианшона.
Применяя теоремы Паскаля и Брианшона к пятиугольникам, четырехугольникам и треугольникам, можно считать, что некоторые вершины слиплись в одну точку. Например, пятиугольник ABCDE можно считать шестиугольником ABCDDE.
Упражнение №33.
Пусть имеется вписанный пятиугольник ABCDE. Докажите, что точки пересечения прямых АЕ и DC, DE и BC, AB и касательной к окружности в точке D лежат на одной прямой;
Докажите, что прямые, соединяющие вершины треугольника с точками касания его вписанной окружностью противолежащей стороны, пересекаются в одной точке.
Рассмотрим треугольник АВС. Пусть О – центр его описанной окружности, E, D и F – середины его сторон, А1, В1, С1 – основания его высот, Н – его ортоцентр, P, Q и R – середины отрезков АН, ВН и СН.
Упражнение №34.
Д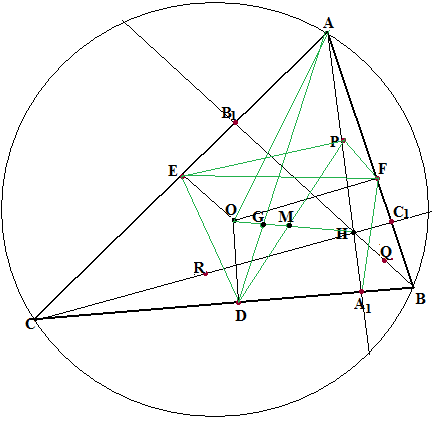 окажите,
что
окажите,
что
АР=OD, OE=BQ, OF=CR;
EDA1F – равнобочная трапеция;
Окружность, проходящая через середины сторон треугольника, проходит также и через середины его высот;
PD служит диаметром как для окружности, проходящей через точки P, D и F, так и для окружности, проходящей через точки P, D и А1.
Все девять точек E, R, D, A1, Q, C1, F, P и B1 лежат на одной окружности. Эта окружность так и называется - окружностью девяти точек. Пусть G=ADOH, M=PDOH. Тогда
GH=2OG, OM=OG.
M – Центр окружности девяти точек.
Радиус окружности девяти точек равен половине радиуса окружности, описанной около треугольника АВС.
G – точка пересечения медиан (центр масс) треугольника АВС.
Упражнение №35.
П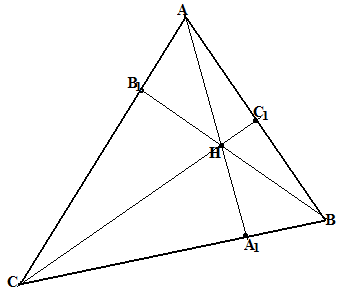 роизведение
отрезков, на которые ортоцентр делит
высоты треугольника, постоянно:
АННА1=ВННВ1=СННС1.
роизведение
отрезков, на которые ортоцентр делит
высоты треугольника, постоянно:
АННА1=ВННВ1=СННС1.
(Consider degree of point H relative circumference of nine points)
Рассматривая степени вершин треугольника АВС относительно окружности девяти точек, выведите следующее тождество:
Упражнение №36.
АА1АН+ВВ1ВН+СС1СН=(а2+b2+c2):2,
Где, как обычно, a, b, c – длины сторон треугольника.
То есть, сумма произведений каждой высоты треугольника на её верхний отрезок равна половине суммов квадратов сторон треугольника.
Упражнение №37.
Докажите, что окружности девяти точек для треугольников АВС, АНС, ВНС и АНВ совпадают. Поэтому и радиусы их описанных окружностей равны.
А как найти их центры (окружностей, описанных около треугольников АНС, ВНС и АНВ)?
В каждой вершине треугольника АВС проведём
пару прямых – биссектрис пар вертикальных
углов, образуемых при этих вершинах
прямыми, содержащими стороны треугольника.
Тогда они сойдутся по три в четырех
точках – центрах вписанной окружности
О и трёх вневписанных окружностей,
касающихся каждая всех трёх прямых,
содержащих стороны треугольника. При
этом прямые ОАА, ОВВ и ОСС
окажутся высотами треугольника ОАОВОС,
а точка О – его ортоцентром. Ортоцентром
же, например, треугольника ООАОВ
является точка ОС. Из вышеприведённого
легко следует, что
каждой вершине треугольника АВС проведём
пару прямых – биссектрис пар вертикальных
углов, образуемых при этих вершинах
прямыми, содержащими стороны треугольника.
Тогда они сойдутся по три в четырех
точках – центрах вписанной окружности
О и трёх вневписанных окружностей,
касающихся каждая всех трёх прямых,
содержащих стороны треугольника. При
этом прямые ОАА, ОВВ и ОСС
окажутся высотами треугольника ОАОВОС,
а точка О – его ортоцентром. Ортоцентром
же, например, треугольника ООАОВ
является точка ОС. Из вышеприведённого
легко следует, что
Упражнение №38.
Описанная окружность треугольника проходит через середины отрезков, соединяющих центры его вписанных окружностей.
Упражнение №39.
Д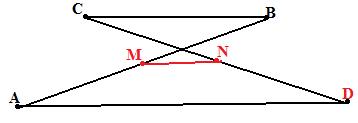 окажите,
что средняя линия трапеции ABCD,
непараллельные стороны которой
пересекаются, равна полуразности её
параллельных сторон.
окажите,
что средняя линия трапеции ABCD,
непараллельные стороны которой
пересекаются, равна полуразности её
параллельных сторон.
Упражнение №40.
С набдим
чертёж упражнения №38 дополнительными
построениями. Отметим середины отрезков,
соединяющих центры трёх вневписанных
окружностей ОА, ОВ и
ОС точками А1, В1 и С1.
Отметим середины отрезков, соединяющих
центры трёх вневписанных окружностей
ОА, ОВ и ОС с
центром вписанной окружности О буквами
К1, К2 и К3. Опустим из
центров вневписанных окружностей ОА,
ОВ и ОС перпендикуляры
ОАА2, ОВВ2 и ОСС2
на прямую ВС. На неё же опустим и
перпендикуляр OD из центра
вписанной окружности О. Тогда OD=r,
ОАА2=r1,
ОВВ2=r2
и ОСС2=r3.
Обозначим радиус описанной окружности
треугольника АВС за R.
Пусть Е=А1К1ВС.
Докажите, что
набдим
чертёж упражнения №38 дополнительными
построениями. Отметим середины отрезков,
соединяющих центры трёх вневписанных
окружностей ОА, ОВ и
ОС точками А1, В1 и С1.
Отметим середины отрезков, соединяющих
центры трёх вневписанных окружностей
ОА, ОВ и ОС с
центром вписанной окружности О буквами
К1, К2 и К3. Опустим из
центров вневписанных окружностей ОА,
ОВ и ОС перпендикуляры
ОАА2, ОВВ2 и ОСС2
на прямую ВС. На неё же опустим и
перпендикуляр OD из центра
вписанной окружности О. Тогда OD=r,
ОАА2=r1,
ОВВ2=r2
и ОСС2=r3.
Обозначим радиус описанной окружности
треугольника АВС за R.
Пусть Е=А1К1ВС.
Докажите, что
A
 1K1=2R,
1K1=2R,A1K1BC,
A1E=(r2+r3):2,
EK1=(r1-r):2
Выведите отсюда, наконец, тождество r1+r2+r3-r=4R
