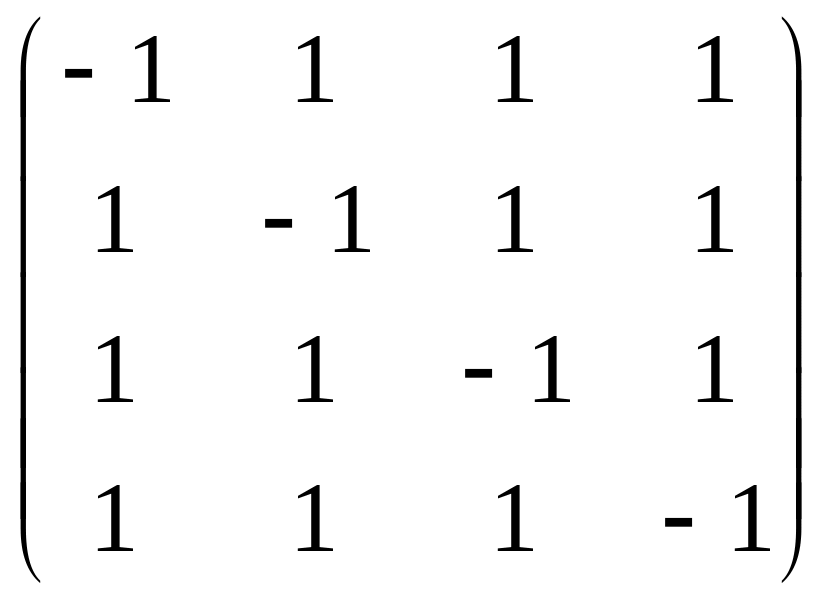25

ГОУ «Школа-интернат Интеллектуал» Абрамсон Я.И. 2006-12-26

(окончание конспекта “Vector Spaces-I”)

1.9. Полилинейные формы.

Мы уже познакомились с линейными формами f:V®K, билинейными формами f: (VV)®K.

Def. Отображение f: (VV´…V)®K называется полилинейным или n-линейным (по числу сомножителей в скобках – экземпляров одного и того же ВП V над полем К) или полилинейной формой, если оно линейно по каждой переменной-вектору при фиксированных остальных (т.е., превращается в линейную форму). Если мы фиксируем все переменные, кроме двух, то получим билинейную форму на этих двух переменных.

Def. Форма f называется знакопеременной, если f(x₁,x₂,...,x_n)=0 всякий раз, когда две каких-либо соседних переменных (векторных!) равны (т.е., x_i=x_i+1 при каком-то i, 1in-1.)

Упражнение 70. Пусть f: (VV)®K – знакопеременная билинейная форма. Докажите, что f(x,y)=-f(y,x).

Упражнение 71. Если мы переставляем два соседних аргумента n-линейной знакопеременной формы, то она меняет знак: f(…,x_i,x_i+1,...)=- f(…, ,x_i+1, x_i,...).

Упражнение 72. Если x_i=x_j для ij, то f(x₁,...,x_n)=0 (т.е., обращается в нуль не только при равенстве двух соседних аргументов, а при равенстве любых двух аргументов).

Упражнение 73. Значение f(x₁,...,x_n) не изменится, если заменить х_i на х_i+aх_j, а все остальные аргументы при этом оставить прежними. Упражнение 74. Найдите выражение для знакопеременной билинейной формы f (v,w), как функции координат векторов v и w, где v,wК² и заданы столбцами матрицы : v=ae₁+ce₂; w=be₁+de₂. На единичной матрице она должна принимать значение 1: . Справившись с этой задачей, сделайте то же самое для знакопеременной трилинейной формы f(v,w,z), где v,w,zК³ и заданы столбцами матрицы 33. Попробуйте распространить ваш результат для n-линейной знакопеременной формы f(x₁,x₂,...,x_n), где все x_iКⁿ и заданы столбцами матрицы nn.

Конспект №16.

Введение в Линейную Алгебру.

Многое из того, что в начале этого конспекта будет излагаться, мы с вами уже прошли на уроках, но, для полноты картины и связности изложения, мне видится целесообразным привести и собрать здесь все те результаты, которые мы в ходе учебного процесса получили. Те же утверждения, которые явно не разбирались на уроках, формулируются, как обычно, в виде упражнений.

1. Матрицы.

Напомним, что обратимыми матрицами (мы рассматриваем квадратные матрицы размером nn над полем F) мы называем те матрицы А, которые имеют левую или правую обратные матрицы, т.е такие матрицы В или С, что ВА=Е или АС=Е, где 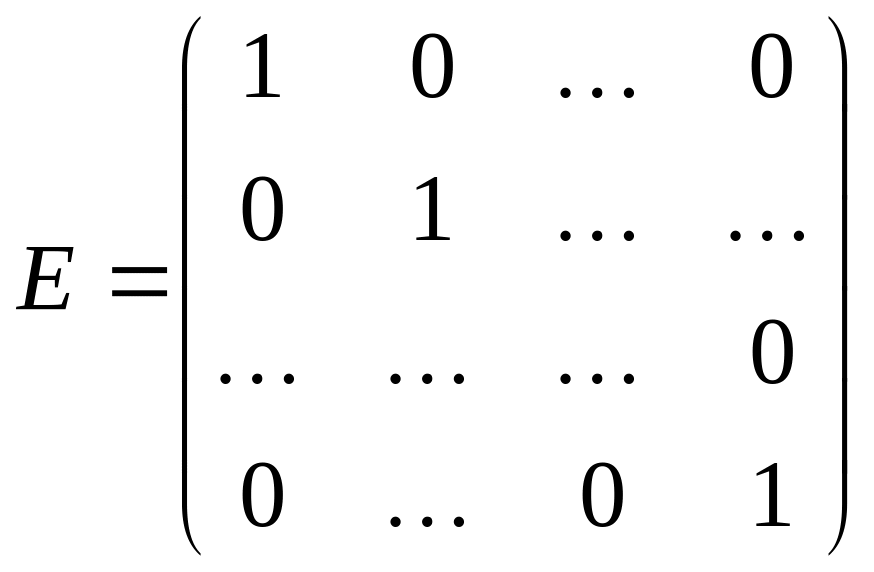. Невырожденными матрицами мы называем матрицы А, чей ранг максимален: RangA=n. Соответственно, все остальные, чей ранг меньше n, называются вырожденными. Иначе говоря, векторы-строки невырожденных матриц (а, следовательно, по теореме о ранге матрицы, и векторы-столбцы) линейно независимы.

Следующее утверждение устанавливает, что если матрица имеет себе обратную с одной стороны (например, слева), то она имеет её же и с другой стороны (несмотря на некоммутативность умножения в кольце матриц).

1.1. Если ВА=Е, то и АВ=Е.

Во-первых, ввиду изоморфизма матриц nn над полем F и линейных операторов (линейных преобразований векторного n-мерного пространства) n-мерного линейного пространства V (над полем F) с фиксированным базисом, это означает В(А(Х))=Х ХV, а, значит, ImA=V, ибо никакой оператор (В) не может увеличить размерность пространства (максимального числа линейно независимых векторов в нём). Отсюда сразу следует, что kerA=kerB=0. С другой стороны, Е коммутирует со всеми матрицами, так что ВЕ=ЕВ. Поскольку ВА=Е, то отсюда В(ВА)=(ВА)В=В(АВ); В(ВА-АВ)=0ВА-АВ=0ВА=АВ=Е.

Мы не могли непосредственно применить здесь упражнение 25 из конспекта «Введение в теорию групп», ибо там содержалось требование, чтобы у всех элементов существовали правые обратные. У нас же, во-первых, не все матрицы вообще обратимы, а во-вторых, априори (заранее) могло бы быть так, что некоторые матрицы обратимы только слева, а другие – только справа. Как следствие, из только что доказанной теоремы получаем: множество всех обратимых матриц порядка nn над полем F образует группу (по умножению). Эта группа обозначается как GL(n,F) и называется полной линейной группой.

Если матрица A=(a_i,j) вырождена, и, если рассматривать её столбцы, как векторы – образы векторов стандартного базиса e₁=(1,0,0,…0); e₂=(0,1,0,0,…0); …; e_n=(0,0,…0,1), то она станет матрицей линейного оператора, который перевёл всё пространство V в некоторое его собственное подпространство и потому обратного оператора иметь не может (вернуть полученную систему линейно зависимых векторов в исходный базис не удастся ввиду леммы «о двух системах векторов»). С другой стороны, если она невырождена, то соответствующий ей линейный оператор перевёл стандартный базис е=(e₁, e_2,…,e_n) в некоторый базис f=(f₁, f_2,…,f_n) и потому имеет обратный оператор, который однозначно определён тем, что «возвращает» вектора нового базиса обратно на место: A^-1:fe. Значит, и сама матрица обратима. Итак, множество всех обратимых матриц совпадает с множеством всех невырожденных матриц.

Будем рассматривать теперь только невырожденные матрицы.

1.2. Поставим вопрос: какова должна быть матрица B_i,j(l), чтобы в результате её умножения слева на матрицу А к элементам i-ой строки матрицы А прибавлялись бы элементы j-ой строки, умноженные на l. Легко находим, что этой матрицей должна быть матрица

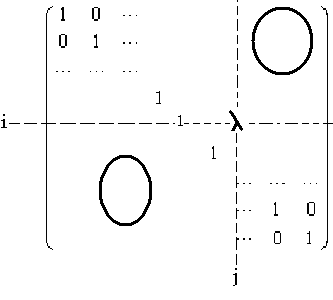
В частности, B_i,j(l)B_i,j()=B_i,j(l+), откуда, между прочим, следует, что при фиксированных индексах i и j матрицы B_i,j(l) образуют группу (по умножению), изоморфную аддитивной группе поля F.

Матрицы, которые могут быть записаны как произведения нескольких матриц B_i,j(l) при всевозможных i j и lF образуют группу SL(n,F) называемую унимодулярной группой. Упражнение 0. Почему они образуют группу? Говорят, что элементарные матрицы B_i,j(l), ij порождают унимодулярную группу. Наша цель – подобрать к данной невырожденной матрице А такую унимодулярную матрицу В, чтобы при умножении её слева на матрицу А получилась матрица как можно более простого вида. Поскольку А невырождена, в первом столбце найдётся 0 элемент. Поэтому можно умножением на элементарную матрицу B_2,j(l) добиться того, чтобы a_2,10. После этого нетрудно добиться того, чтобы a_1,1=1.

Упражнение 1. На какую элементарную матрицу В₁,₂(*) надо для этого умножить слева матрицу А?

Добившись этого, мы затем легко добьемся того, чтобы в первом столбце матрицы А все остальные элементы стали равными нулю и матрица приобрела следующий вид: Упражнение 2. Что надо для этого делать?

Теперь перейдем ко второму столбцу и спустимся на строку вниз:

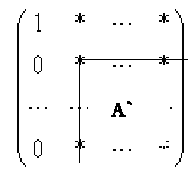
В отмеченной подматрице A` в первом столбце должны иметься ненулевые элементы. Упражнение 3. Почему?

Поэтому можно устроить (естественно, умножением слева на элементарную матрицу!) так, чтобы a_3,20. А уж после этого, тем же приёмом, что и выше, сделать a_2,2=1. Сделав это, мы снова все остальные элементы второго столбца (включая и a_1,2) умножениями на подходящие элементарные матрицы обнуляем: .

Продолжая в том же духе, мы, в конце концов, придём к матрице .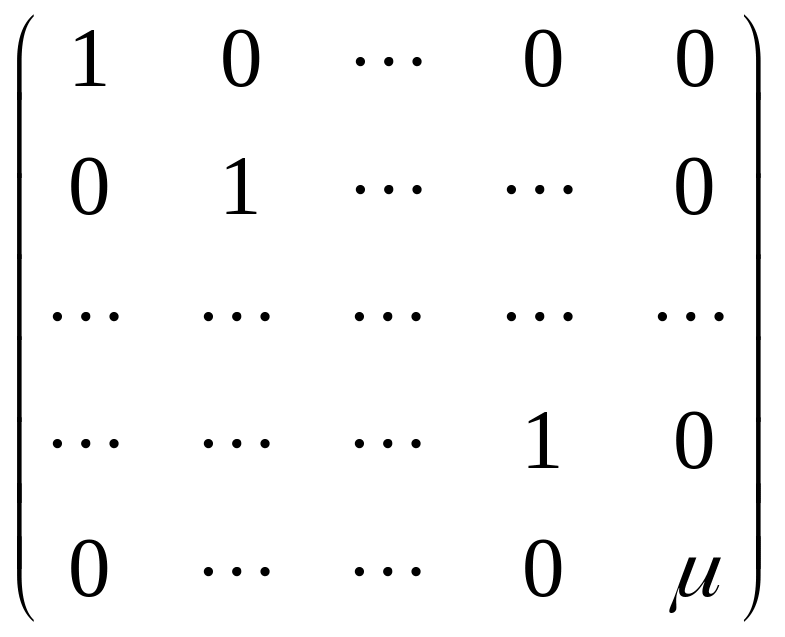

Упражнение 4.

Элемент a_n,n=0 (почему?) Но его, в отличие от предыдущих диагональных элементов, мы уже не можем сделать равным 1. Каким же образом мы тогда добиваемся равенства нулю всех остальных элементов последнего столбца?

Итак, мы доказали теорему: для произвольной невырожденной матрицы А можно умножением на подходящую унимодулярную матрицу слева добиться того, что она станет равной матрице D() которая от единичной матрицы отличается только тем, что у неё в правом нижнем углу стоит некоторый ненулевой элемент  поля F. BA=D(); или, иначе говоря, каждая невырожденная матрица А представима (разлагается в произведение) в виде А=ВD(), где ВSL(n,F) – унимодулярная матрица.

Матрицы D обладают следующим свойством: Упражнение 5. D()D()=D(). (Проверьте). Упражнение 6. Пусть нужно умножить i-ую строку матрицы А на некоторый элемент  поля F. Как выглядит матрица B_i() умножение на которую слева осуществляет это действие?

Упражнение 7.

Как, умножениями слева на элементарные матрицы вида B_i,j(l), i≠j, и, если необходимо, ещё на матрицу B_i(-1), добиться перестановки i-ой и j-ой строк матрицы А? Напишите соответствующую последовательность умножений и результирующую матрицу.

Комбинируя умножения на элементарные матрицы вида B_i,j(l) и матрицы вида B_i(l), мы в конце концов, любую невырожденную матрицу А превратим в единичную: В₁В₂...В_rA=E. Умножим справа это равенство на матрицу А^-1, обратную к А:

В₁В₂...В_rAА^-1=EА^-1 или В₁В₂...В_rЕ=А^-1.

Таким образом, мы получаем способ построения матрицы, обратной к данной матрице А: надо производить с матрицей А элементарные преобразования – прибавлять к одной строке линейную комбинацию других, переставлять строки местами, умножать строки на числа, стараясь превратить матрицу А в единичную матрицу и параллельно производить те же действия над единичной матрицей. В тот момент, когда матрица А станет единичной, единичная матрица превратится в обратную к ней.

Упражнение 8.

Найдите матрицу, обратную к матрице А= .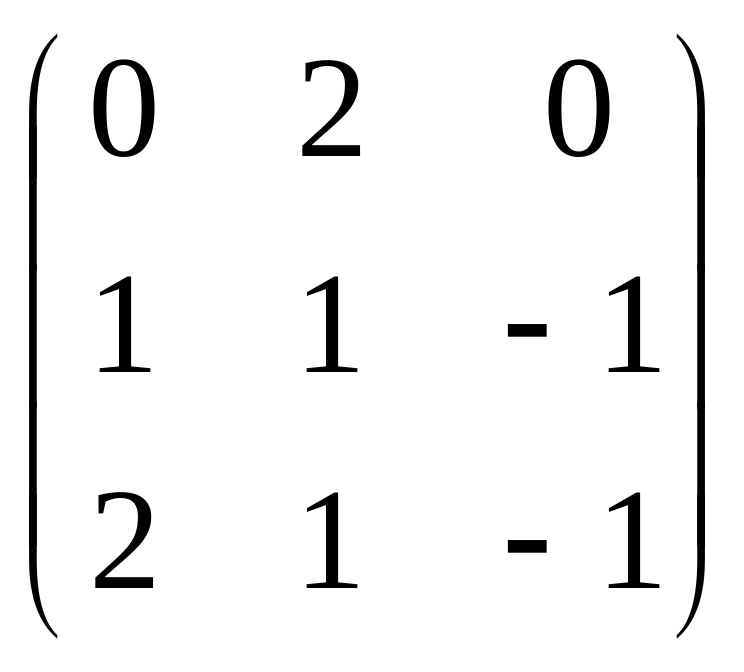

Упражнение 9.

Найдите матрицу, обратную к матрице А=