Упражнение №41.

Пусть в треугольнике АВС точка О – центр описанной окружности, I - центр вписанной окружности, J - центр вневписанной окружности. Опустим из I и J перпендикуляры IF и JH на прямую АВ и проведём через О диаметр DE. Пусть R – радиус описанной окружности, r - радиус вписанной окружности, d – расстояние между их центрами. Докажите, что

1. D – центр описанной окружности треугольника IBJ;

2. Степень I относительно окружности О равна d²-R², откуда AIID=R²-d²;

3. Из AIFBDF имеем AIBD=EDIF;

4. Выведите тождество Эйлера d²=R(R-2r).

Между прочим, непосредственным следствием из тождества Эйлера вытекает неравенство R>2r, доказанное нами ранее.

На предыдущем чертеже, обозначив растояние IJ через d₁, а радиус окружности J как r₁, рассмотрите степень J относительно окружности О и треугольники AHJ и BED.

Получите тождества:

Упражнение №42.

1. 

2. 

Следующее утверждение не является новым, оно уже встречалось и доказывалось нами ранее, но времени с тех пор прошло достаточно, чтобы успеть его забыть и, помня, что повторение – мать учения, передокажем его снова, тем более, что оно и важно и полезно.

Упражнение №43. (Прямая Симсона)

Если из какой-либо точки окружности, описанной около треугольника, опущены перпендикуляры на его стороны, то основания этих перпендикуляров лежат на одной прямой;

Если основания перпендикуляров, опущенных из некоторой точки на стороны треугольника лежат на одной прямой, то эта точка лежит на окружности, описанной около треугольника.

Р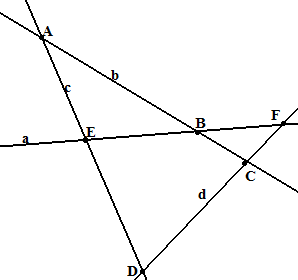 ассмотрим на плоскости конфигурацию из четырёх прямых, находящихся «в общем положении». Это значит, что никакая пара из них не параллельна и никакая тройка из них не инцидентна одной точке.

Такая конфигурация называется полным четырехсторонником.

В этой конфигурации присутствует один четырехугольник и четыре треугольника. Например, на рисунке это будут треугольники ABE, ACD, FBC и FED.

Упражнение №44.

Докажите, что все четыре окружности, описанные около этих треугольников пересекаются в одной точке.

Сейчас займёмся процедурой, которая приведёт нас к важному выводу из предыдущего упражнения, хотя носить она будет пока что неформальный характер. Формализовать её и превратить в строгое математическое рассуждение позволит топология, которую мы будем проходить в курсе алгебры (хотя она и относится в высшей математике к области геометрии). Начнём двигать прямую а (например) в сторону прямой d, не трогая остальные три прямых, так, что точка В приближается к точке С, а точка Е к точке D. Подумав, что при этом будет происходить с окружностями, и что должно получиться «в пределе», когда точки-таки сольются, получите следующий результат:

Упражнение №45.

1. Если две окружности, касающиеся разных сторон угла, пересекаются на окружности, проходящей через вершину угла и обе точки касания, то они пересекаются вторично на прямой, проходящей через точки касания;

2. Если две окружности, касающиеся разных сторон угла, пересекаются на прямой, проходящей через точки касания, то они пересекаются вторично на окружности, проходящей через вершину угла и обе точки касания.

Упражнение №46.

В прямоугольном треугольнике АВС из вершины прямого угла проведена высота BD. Известно, что CD<AD. Точка МCD такова, что из отрезков AD, AM и BM можно составить прямоугольный треугольник. В каком отношении точка М делит отрезок CD?

Следующие 11 задач нам предстоит решать вместе, так как я не имел времени, чтобы над ними подумать. А, может быть, и все равно не решил бы, даже если бы и имел. Если они окажутся нам не под силу, мы их пропустим.

Упражнение №47.

Прямая, соединяющая основания высот, опущенных из двух вершин треугольника, перпендикулярна к радиусу описанного круга, проведённого к третьей вершине.

Упражнение №48.

Ортоцентр треугольника служит центром подобия его описанной окружности и окружности девяти точек.

Упражнение №49.

Если из какой-либо точки окружности построить три хорды и на них, как на диаметрах, построить три окружности, то вторые точки пересечения этих окружностей расположены на одной прямой. (Автор рекомендует опираться на прямую Симсона).

Упражнение №50. (Теорема Микеля)

На окружности отметили четыре точки, А, В, С и D. Через точки А и В, В и С, С и D, D и A провели четыре окружности. Вторые точки пересечения этих окружностей также лежат на одной окружности.

Упражнение №51.

Окружность, построенная на отрезке, соединяющим центры двух непересекающихся окружностей, как на диаметре, проходит через четыре точки пересечения внешних общих касательных к этим окружностям с их общими внутренними касательными.

Упражнение №52.

Докажите, что четырехугольники не определяются однозначно серединами их сторон, но все четырехугольники с данными серединами сторон равновелики.

Упражнение №53.

Докажите, что пятиугольник серединами его сторон определяется однозначно и укажите способ его построения.

Упражнение №54.

Построить точку, касательные из которой к двум заданным окружностям равны и составляют заданный угол.

(Автор рекомендует определить сначала на радикальной оси точку, которая вместе с исходной точкой и центрами окружностей образует вписанный четырехугольник).

Упражнение №55.

Построить окружность, диаметральную к заданной и проходящую через две заданные точки.

Упражнение №56.

Построить окружность так, чтобы касательные к нему из трёх заданных точек были бы конгруэнтны трём заданным отрезкам.

Упражнение №57.

Построить окружность так, чтобы она, пересекаясь с заданной окружностью, определила бы общую хорду, конгруэнтную заданному отрезку.

Упражнение №58 (C4)

На стороне ВА угла АВС, равного 30 градусам, взята точка D такая, что AD=2, BD=1. Найдите радиус окружности, касающейся прямой ВС и проходящей через точки А и D.

(Answer: 1 and 7).

Упражнение №59.

П олуокружность радиуса r разделена точками на 3 равные части и точки деления соединены хордами с одним и тем же концом диаметра, стягивающего эту полуокружность. Найдите площадь фигуры, ограниченной двумя хордами и заключённой между ними дугой.

Упражнение №60.

На сторонах АВ и AD параллелограмма ABCD взяты соответственно точки E и F так, что EF||BD. Докажите, что треугольники BCE и CDF равновелики.

Упражнение №61.

Н а лучах АВ и AD, на продолжениях сторон АВ и AD параллелограмма ABCD, взяты произвольно точки E и F. Прямые BF и ED пересекаются в точке О. Докажите, что четырехугольники CEOF и OBAD равновелики.

Упражнение №62.

На стороне AD параллелограмма ABCD взята произвольно точка N и проведены прямые NK||AC и NM||BD до пересечения со сторонами параллелограммав точках К и М. Докажите, что треугольники NMB и NKC равновелики.

Упражнение №63.

Выведите формулу, выражающую площадь произвольного четырехугольника (в том числе и невыпуклого), через его диагонали и синус угла между ними,

Упражнение №64.

Площадь четырехугольника ABCD равна S. E=ABCD. AM:AC=BN:BD=k. Найдите площадь треугольника ЕМN. (Hint: Find XBC| BX:BC=k and draw XM||AB and XN||CD. Show then, that S(EMN)=S(BCNM) and exploit the formula, found in the previous exercise). Answer: k(1-k)S.

Упражнение №65.

Через вершину выпуклого четырехугольника проведите прямую, которая делит его на две равновеликие части. (Start from broken line AOC which does the job)

Упражнение №66.

Н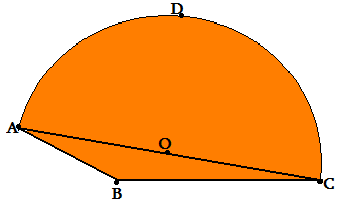 а стороне треугольника, как на диаметре, внешним образом построен полукруг. Проведите прямую, которая делит полученную фигуру на две равновеликие части.

Упражнение №

На сторонах AD и ВС параллелограмма ABCD взяты произвольно точки К и М. Найдите ГМТ L таких, что ломаная KLM делит параллелограмм на две равновеликие части.

Упражнение № 67*.

В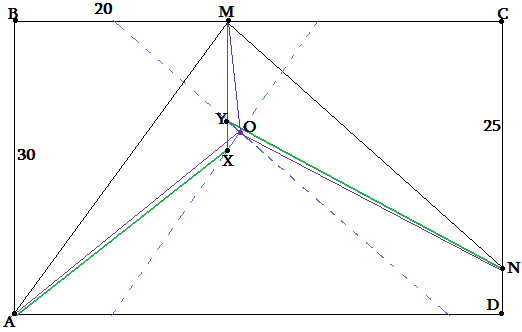 ерх и боковые стороны прямоугольного торта 3045 покрыты глазурью. Разделите торт на три куска равного объёма так, чтобы горизонтальное сечение каждого куска представляло собой четырехугольник, и количество глазури на каждом куске было одинаковым.

Упражнение №68.

Н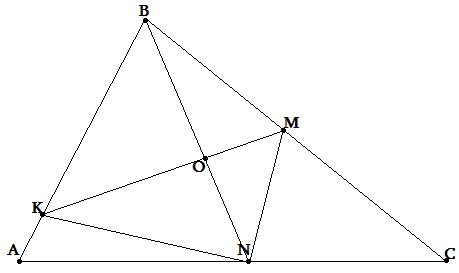 а сторонах АВ и ВС треугольника АВС отмечены точки К и М так, что АК:КВ=1:4, ВМ:МВ=4:5. На отрезке КМ выбрана точка О так, что КО:ОМ=3:1. Расстояние от точки О до стороны АС равно d, а длина стороны АС равна а. Найдите площадь треугольника KMN, где N=ACBO.

Упражнение №69.

Через произвольную точку на стороне треугольника проведите прямую, которая делит его на две равновеликие части.

Упражнение №70.

Постройте треугольник, равновеликий данному многоугольнику.

Упражнение №71.

В трапеции ABCD с меньшим основанием ВС через точку В проведена прямая, параллельная CD и пересекающая диагональ АС в точке Е. Площадь треугольника ABC равна S. Найдите площадь треугольника СЕD.

Упражнение №72.

BD – высота в остроугольном треугольнике АВС, МАС, GAB, AM=MC и MGAC. Найдите площадь четырехугольника BGDC если площадь треугольника АВС равна 10.

Упражнение №73.

Четырехугольник ABCD – выпуклый, GBD, BG=GD, GH||AC, HCD, S(ADH)=8. Найдите площадь четырехугольника ABCD.

Упражнение №74.

Сторона ВС остроугольного треугольника АВС разбита точками H, G и E на четыре равные части: BE=EG=GH=HC. Из этих точек проведены прямые HF, GK и EL, параллельные высоте AD, причём F и KAC, а LAB. Докажите, что прямые DF, DK и DL разбивают треугольник АВС на четыре равновеликие фигуры.

Упражнение №75.

На диагонали АС параллелограмма ABCD отмечена произвольная точка N и через вершину С проведена прямая параллельно BN до пересечения с продолжением стороны AD в точке Е. Докажите, что треугольники ANE и CDE равновелики.

Упражнение № 76**. (финал VI Олимпиады им. И.Ф. Шарыгина)

В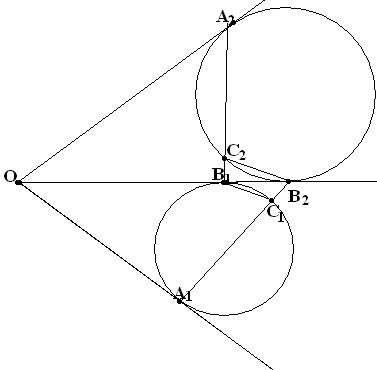 равные углы Х₁ОУ и УОХ₂ вписаны окружности ₁ и ₂, касающиеся сторон ОХ₁ и ОХ₂ в точках А₁ и А₂ соответственно, а стороны ОУ – в точках В₁ и В₂. Прямая А₁В₂ пересекает второй раз окружность ₁ в точке С₁, а прямая А₂В₁ пересекает второй раз окружность ₂ в точке С₂. Докажите, что С₁С₂ – общая касательная к окружностям.

(Hint: first, prove that angular measure of A₂B₂ is equal to the angular measure of B₁A₁. Then find congruent triangles and prove, that A₁B₂=A₂B₁. Turn now to the properties of a secant and a tangent and come to B₂C₁=B₁C₂. Find out, that A₂C₂B₂+A₁C₁B₁= and conclude, that B₁C₁B₂C₂ is inscribed isosceles trapezoid. Finally, remember about an angle between a chord and a tangent and the converse theorem)

Упражнение № 77**. (из вступительных экзаменов на мехмат МГУ)

В треугольнике АВС сторона АВ=38, а медиана СМ=19 и наклонена к АВ под углом 40. В этот треугольник вписали окружность. Найдите периметр треугольника, вписанного в эту окружность и подобного треугольнику АВС.

(It is beautiful problem and solves easily once you find a key idea. Remember, that in right triangle r=a+b-c and ab=hc, where h is the height, drawn from the vertex of the right anle. The answer is 38sin40)

Упражнение №78.

Внутри угла АОВ дана точка М. Проведите через точку М прямую ХУ, пересекающую

стороны угла в точках Х и У так, чтобы точка М была серединой отрезка ХУ. (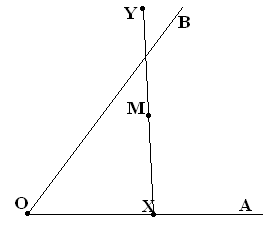 Consider the set of points Y | XM=MY when X runs along OA)

У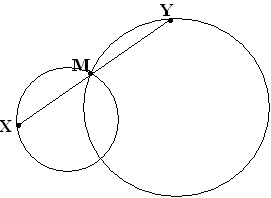 пражнение №79.

Через общую точку двух окружностей проведите прямую так, чтобы окружности высекали на ней равные, не совпадающие хорды. (Let point X run round circumference)

Упражнение №80.

Д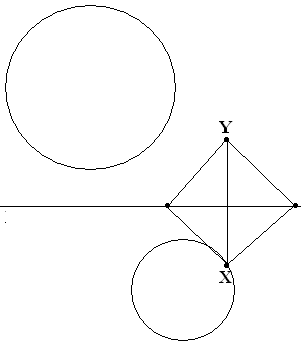 ана прямая и две окружности по разные стороны от неё. Постройте квадрат, две противоположные вершины которого лежали бы на этих окружностях, а две другие – на этой прямой.

Упражнение №81.

Д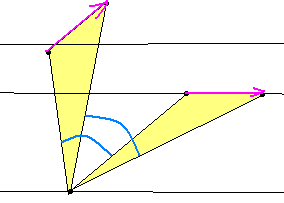 аны три параллельные прямые. Постройте равносторонний треугольник так, чтобы на каждой из этих прямых лежала одна его вершина.

Упражнение №82.

Постройте треугольник по трём его медианам, конгруэнтным заданным отрезкам.

1 По одноименному учебнику Н.А.Извольского, Учпедгиз, 1941.

2 Этот термин в дальнейшем получит своё точное математическое содержание

15