
- •Дифференциальное исчисление функций одной переменной
- •2. Правила дифференцирования
- •3. Касательная и нормаль к плоской кривой.
- •5. Производная неявно заданной функции
- •Свойства дифференциала.
- •10. Остаточный член формулы Тейлора
- •11. Вывод формулы Тейлора
- •13. Экстремум необходимое и достаточное условие существования экстремума функции.
Свойства дифференциала.
Если u = f(x) и v = g(x)- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u v) = (u v)dx = udx vdx = du dv
2) d(uv) = (uv)dx = (uv + vu)dx = vdu + udv
3) d(Cu) = Cdu
4)
![]()
Геометрический смысл дифференциала.
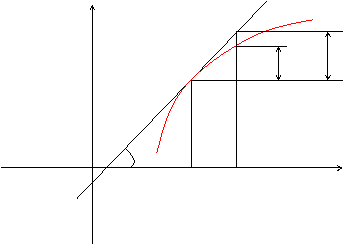
Из треугольника MKL: KL = dy = tgx = yx
Таким образом, дифференциал функции f(x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
7. Производные высших порядков.
Рассмотрим функцию
![]() ,
определенную на некотором промежутке
,
определенную на некотором промежутке
![]() .
Вычислим производную
.
Вычислим производную
![]() ,
которая также является функцией на
.
Производной второго порядка от функции
называется
производная от ее производной:
,
которая также является функцией на
.
Производной второго порядка от функции
называется
производная от ее производной:
![]() .
Аналогично определяют производную
любого порядка:
.
Аналогично определяют производную
любого порядка:
![]() .
.
Дифференциалы высших порядков.
Рассмотрим дифференциал
функции
в
произвольной точке промежутка
:
![]() .
Здесь
.
Здесь
![]() -
приращение
независимой переменной, которое является
числом и не зависит от
-
приращение
независимой переменной, которое является
числом и не зависит от
![]() .
Сам же дифференциал есть функция от
,
и можно вычислить дифференциал от этой
функции:
.
Сам же дифференциал есть функция от
,
и можно вычислить дифференциал от этой
функции:
![]() При
При
![]() этот
дифференциал от дифференциала называется
дифференциалом второго порядка и
вычисляется по формуле
этот
дифференциал от дифференциала называется
дифференциалом второго порядка и
вычисляется по формуле
![]() Аналогично
вычисляется дифференциал любого порядка
Аналогично
вычисляется дифференциал любого порядка
![]() .
.
Лейбница
формула, формула, выражающая производную
n-го порядка (см. Дифференциальное
исчисление) от произведения
двух функций через производные
сомножителей:
![]() .
.
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
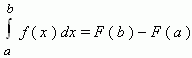
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
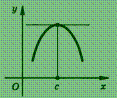
8. Теорема Ферма. Если функция у = f (х), определенная в интервале (а ; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический смысл этой
теоремы состоит в том, что касательная
к графику функции у
= f
(х)
в точке с абсциссой с
параллельна оси абсцисс (рис.).
 Теорема
Ролля. Если функция
у
= f
(х),
непрерывная на отрезке [а
; b]
и дифференцируемая в интервале (а
; b),
принимает на концах этого отрезка равные
значения f
(a)
= f
(b),
то в интервале (а
; b)
существует такая точка с,
что f
′(с)
= 0.
Геометрически эта теорема означает
следующее: если крайние ординаты
кривой у
= f
(х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
Теорема
Ролля. Если функция
у
= f
(х),
непрерывная на отрезке [а
; b]
и дифференцируемая в интервале (а
; b),
принимает на концах этого отрезка равные
значения f
(a)
= f
(b),
то в интервале (а
; b)
существует такая точка с,
что f
′(с)
= 0.
Геометрически эта теорема означает
следующее: если крайние ординаты
кривой у
= f
(х)
равны, то на кривой найдется точка, в
которой касательная параллельна оси
абсцисс (рис.).
 Теорема
Лагранжа. Если функция
у
= f
(х)
непрерывна на отрезке [а
; b]
и дифференцируема в интервале (а
; b),
то в этом интервале найдется такая точка
с,
что
Теорема
Лагранжа. Если функция
у
= f
(х)
непрерывна на отрезке [а
; b]
и дифференцируема в интервале (а
; b),
то в этом интервале найдется такая точка
с,
что
![]()
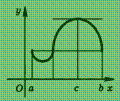
Эта теорема имеет простой
геометрический смысл (рис.): на графике
функции у
= f
(х)
между точками А
и В
найдется такая внутренняя точка С,
что касательная к графику в точке С
параллельна хорде АВ.
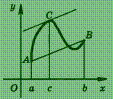
Следствие. Если f ′(x) = 0 в интервале (а ; b), то в этом интервале функция f (х) постоянна.
9. Теорема Коши. Если функции f (х) и g (х): 1) непрерывны на отрезке [а ; b];
2) дифференцируемы в интервале (а ; b);
3) g'(x) ≠ 0 в этом интервале,
то в интервале (а ; b) существует такая точка с, что имеет место равенство
![]()
Правило Лопиталя.
Пусть
при x![]() a
для f(x) и g(x),
дифференцируемых в некоторой окрестности
точки a, выполняются условия:
a
для f(x) и g(x),
дифференцируемых в некоторой окрестности
точки a, выполняются условия:
1. либо f(x)
0,
g(x)
0,
либо f(x)
![]() ,
g(x)
;
2. существует предел
limx
,
g(x)
;
2. существует предел
limx![]() af
af![]() (x)g
(x).
(x)g
(x).
Тогда limx af(x)g(x)=limx af (x)g (x).
Правило Лопиталя, как говорят математики,
позволяет избавляться от неопределенностей
типа:
00 или
![]() .
.
Неопределенности вида 0 ·
![]() ,
–
,
0 0,
0,
1
,
–
,
0 0,
0,
1
![]() часто
удается свести к неопределенностям
вида 00 или
с
помощью различных тождественных
преобразований. После этого можно
применять правило Лопиталя.
часто
удается свести к неопределенностям
вида 00 или
с
помощью различных тождественных
преобразований. После этого можно
применять правило Лопиталя.
Рассмотрим некоторые из возможных преобразований указанных неопределенностей.
1.
−
: пусть f(x)![]() ,
g(x)
,
тогда данная неопределённость
приводится к типу 00 следующим
преобразованием: f(x)−g(x)=1f(x)
,
g(x)
,
тогда данная неопределённость
приводится к типу 00 следующим
преобразованием: f(x)−g(x)=1f(x)![]() g(x)1g(x)−1f(x),
g(x)1g(x)−1f(x),
2.
![]() 0 :
пусть f(x)
,
g(x)
0 ,
тогда данная неопределенность
приводится к типу: 00 или
с
помощью преобразований:
f(x)
g(x)=1g(x)f(x)=1f(x)g(x).
0 :
пусть f(x)
,
g(x)
0 ,
тогда данная неопределенность
приводится к типу: 00 или
с
помощью преобразований:
f(x)
g(x)=1g(x)f(x)=1f(x)g(x).
Остальные неопределенности приводятся к первым двум с помощью логарифмического преобразования: logaf(x)g(x)=g(x) logaf(x) .
Если после применения правила Лопиталя неопределенность типа : 00 или осталась, нужно применить его повторно. Многократное применение правила Лопиталя может привести к требуемому результату. Правило Лопиталя применимо и в случае, если x a .
