Дисперсия альтернативного признака
Обозначим через w долю единиц совокупности, обладающих альтернативным признаком, q – долю единиц, не обладающих этим признаком, то (w + q) = 1.
Обозначим наличие признака у единиц совокупности цифрой 1, отсутствие признака – 0. Тогда средняя величина альтернативного признака будет определяться по формуле
,
т. е. среднее значение альтернативного признака равно доле единиц совокупности, обладающих этим признаком.
Дисперсия альтернативного признака рассчитывается по формуле
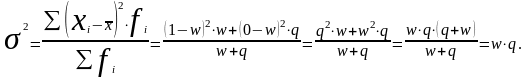
Таким образом, дисперсия альтернативного признака равна произведению доли единиц совокупности, обладающих исследуемым признаком, на долю единиц совокупности, не обладающих этим признаком.
Пример 13. На экзамене по статистике в одной из групп ЭМФ, состоящей из 25 студентов, 22 студента успешно сдали экзамен, а остальные – не сдали экзамен. Вычислить дисперсию и среднее квадратическое отклонение.
Решение. Определим долю студентов, успешно сдавших экзамен (w)
.
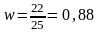Значит, дисперсия признака равна
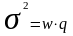= 0,88
=
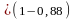0,1056.
Вычислим среднее квадратическое отклонение
=
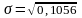0,325.
Характеристика закономерностей рядов распределения
Изменение частот в вариационных рядах называют закономерностями распределения. Кривая распределения – графическое изображение в виде непрерывной линии изменения частот в вариационном ряду.
Уравнение нормальной кривой имеет следующий вид:
у
(t)
=
,
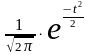где у (t) – ордината кривой нормального распределения;
t
– нормированное отклонение, равное
t
=
;
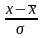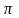– число
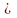3,1415;
e – число 2,7182.
Различают следующие виды кривых распределения:
– одновершинные (симметричные и асимметричные);
– многовершинные.
При симметричном
распределении частоты любых двух
вариантов, равностоящих в обе стороны
от центра распределения, равны между
собой, т. е.
=
=
.
Для сравнительного
изучения асимметрии
распределений вычисляют относительный
показатель
асимметрии
(
)
по формулам
=
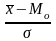или
=
.
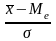При правосторонней
асимметрии
<
<
,
> 0.
При левосторонней асимметрии > > , < 0.
Степень асимметрии
можно определить как отношение момента
третьего порядка к среднему квадратическому
отклонению в кубе по формуле
=
.
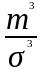Асимметрия выше 0,5 (без учета знака) считается значительной, меньше 0,25 – незначительной.
Для нормального распределения характерны следующие зависимости:
R
=
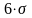и
=
.
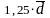Под эксцессом распределения понимается высоковершинность или низковершинность распределения по сравнению с нормальным распределением.
При высоковершинности наблюдается скопление частот в середине ряда, а при низковершинности – разбросанность частот ряда.
Для характеристики степени эксцесса применяется коэффициент эксцесса (Е)
Е
=
,
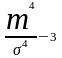где
– момент четвертого порядка
.
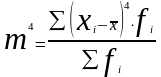Если Е = 0 – нормальное распределение;
Е > 0 – выше нормального;
Е < 0 – ниже нормального.