Функции нескольких переменных (фнп)

1. Фнп, их определение, обозначение и область определения

1. Переменная называется функцией многих (нескольких) переменных (аргументов) , если каждой системе значений из области их изменения соответствует одно или несколько значений .

Функциональная зависимость от символически обозначается

,

где после символа функции в скобках указываются все переменные, от которых зависит данная функция.

В частном случае:

2. Если каждой паре независимых друг от друга чисел (х, у) из некоторого множества по какому-либо правилу ставится в соответствие одно или несколько значений переменной z, то переменная z называется функцией двух переменных.

3. Если каждой системе значений соответствует одно значение , то функция называется однозначной, а если более одного, то – многозначной.

Частное значение функции при обозначается . Например, если , то .

Геометрически:

- каждая система значений двух переменных изображается точкой на плоскости, а функция двух переменных - некоторой поверхностью в пространстве;

- система значений трех переменных изображается точкой в пространстве (абсцисса, ордината, аппликата).

Система значений четырех и большего числа переменных не имеет геометрического изображения. Однако в целях общности, для упрощения записей и рассуждений:

4. систему значений любого числа n переменных называют точкой n-мерного пространства ( ) , а функцию , зависящую от n переменных называют функцией точки n-мерного пространства .

5. Областью определения функции называется совокупность всех точек, в которых она имеет определенные действительные значения ( существует).

Геометрически:

- область определения функции двух переменных представляет некоторую совокупность точек плоскости;

- а для функции трех переменных трех переменных – некоторую совокупность точек пространства.

ФНП может быть задана аналитически (формулой), геометрически (для функции двух переменных) и таблицей.

Примеры.

1.Вычислить частное значение функции:

а) при

б) в

2.Построить область изменения переменных и , заданную неравенствами:

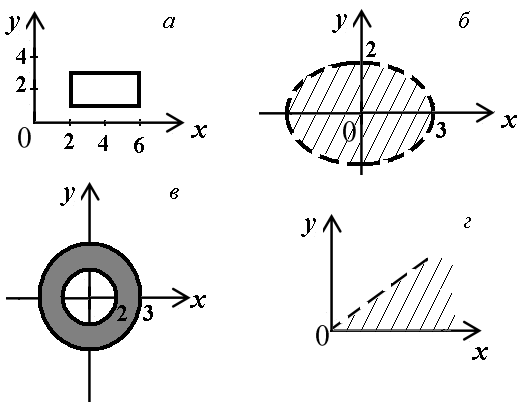
а) , .

Этим неравенствам удовлетворяют координаты каждой точки, находящейся внутри и на границе прямоугольника, стороны которого лежат на прямых , . Этот прямоугольник и есть область изменения переменных и (рис. а). Такая область, в которую входит и ее граница, называют замкнутой.

б) .

Данная область – совокупность всех точек, лежащих внутри эллипса . Область открытая (рис. б).

в) .

Данная область – круговое кольцо, ограниченное окружностями и с общим центром в начале координат и радиусами, равными 2 и 3. Область замкнутая (рис. в).

г) .

Открытая область, ограниченная биссектрисой первого координатного угла и осью абсцисс (рис. г).

3.Найти область определения функций:

а) .

. Геометрическое изображение этой функции (график) – это плоскость, пересекающая координатные оси в точках , и .

б) .

Из условия, что знаменатель не должен обращаться в нуль: находим и одновременно. Отсюда: область определения данной функции – вся числовая плоскость, за исключением точки .

в) .

Из условия, что подкоренное выражение быть неотрицательным: находим . Отсюда: область определения данной функции – круг с центром в точке и радиусом . (Внутри круга подкоренное выражение положительно, на его границе – равно нулю, а вне круга – отрицательно.)

Графическим изображением данной функции является полусфера, расположенная над плоскостью хОу (р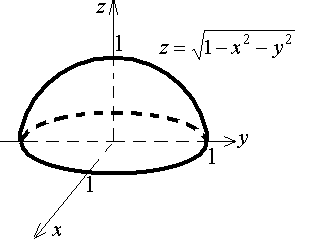ис.2).

Рис. 2.

в) .

Область определения этой функции находим из условия . Точки, удовлетворяющие этому неравенству, лежат внутри I и III квадрантов.

г) .

Область определения этой функции – вся числовая плоскость, за исключением прямой .

е) .

Область определения этой функции – совокупность значений и , удовлетворяющих неравенствам . На плоскости хОу эта область представляет собой полосу, ограниченную параллельными прямыми и .