
- •Функции нескольких переменных (фнп)
- •1. Фнп, их определение, обозначение и область определения
- •2. Предел фнп. Непрерывность
- •3. Свойства функций, непрерывных в области
- •4. Частные производные функций нескольких переменных
- •5. Дифференциалы фнп. Геометрический смысл полного дифференциала
- •6. Приближенные вычисления с помощью полного дифференциала. Линеаризация функции
- •7. Дифференцирование сложных функций
- •8. Дифференцирование неявных функций
- •9. Частные производные и дифференциалы высших порядков
- •Геометрические приложения
- •10. Касательная плоскость и нормаль к поверхности. Особые точки
- •11. Экстремумы функции нескольких переменных
- •11.1 Локальный экстремум
- •Скалярное поле
- •1. Скалярное поле. Линии и поверхности уровня
- •2. Производная по направлению
- •Свойства производной по направлению
- •3. Градиент функции
- •Свойства градиента
Свойства производной по направлению
1) Производная определяет величину скорости изменения функции при движении точки М по направлению . Абсолютная величина производной по направлению определяет величину скорости, а знак производной – характер изменения скорости (ее увеличение или уменьшение).
2)
Производная от функции
по положительным
направлениям координатных осей
Ох,
Оу,
Оz
равны ее частным производным
,
и
![]() .
Например, если направление
совпадает с положительным направлением
Ох, то углы, образованные этим вектором
и координатными осями Ох, Оу и Оz
равны соответственно: α=0, β==90.
Тогда, согласно определению, по формуле
(1), получим
.
Например, если направление
совпадает с положительным направлением
Ох, то углы, образованные этим вектором
и координатными осями Ох, Оу и Оz
равны соответственно: α=0, β==90.
Тогда, согласно определению, по формуле
(1), получим
![]() .
.
3) Производные по прямо противоположным направлениям отличаются только по знаку.
4) Производная по направлению линии уровня (по касательной к линии уровня) функции двух переменных и производная по направлению любой линии, лежащей на поверхности уровня (по любому направлению, касательному к поверхности уровня) функции трех переменных равны нулю.
5)
Поле
![]() в точке М в направлении
возрастает
(убывает), если его производная по
направлению
в точке М в направлении
возрастает
(убывает), если его производная по
направлению
 (соответственно
(соответственно
 ).
).
6) Производная по направлению достигает своего наибольшего значения по направлению нормали к поверхности уровня.
Примеры.
1.
Вычислить производную функции
![]() в точке
в точке
![]() по направлению:
по направлению:
а) биссектрисы первой координатной четверти.
б) радиуса-вектора точки А.
в)
вектора
![]() .
.
1) Находим частные производные функции и вычисляем их значения в точке А:
![]() ,
,
![]()
![]() ,
,
![]()
Подставляя
в формулу (1), найдем производные функции
в точке А по любому направлению
![]()
 .
.
2) найдем значения производной по указанным направлениям:
а)
Для
биссектрисы первого координатного угла
![]() ,
откуда искомая производная равна
,
откуда искомая производная равна

б)
запишем координаты радиуса-вектора
точки А:
![]() ,
и найдем направляющие косинусы:
,
и найдем направляющие косинусы:
 ,
,
 .
.
Тогда
для этого случая
 .
.
в)
направляющие
косинусы вектора
:
 ,
,
 .,
.,
откуда
 .
.
2.
Вычислить производную функции
![]() по направлению вектора
по направлению вектора
![]() в любой точке и в точках
в любой точке и в точках
![]() и
и
![]() .
.
1) Находим частные производные функции :
![]() ,
,
![]() ,
,
![]()
и
направляющие косинусы вектора
,
модуль которого
![]() :
:
 ,
,
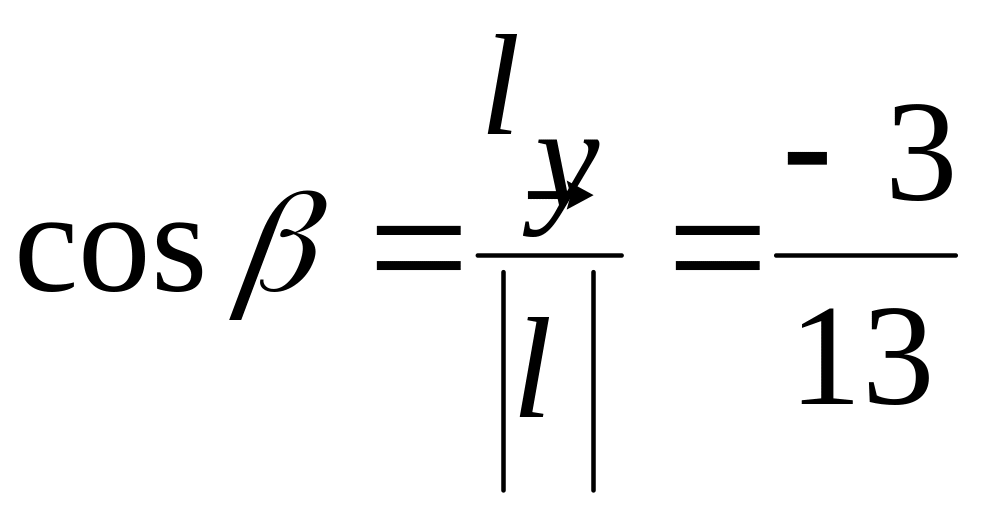 ,
,
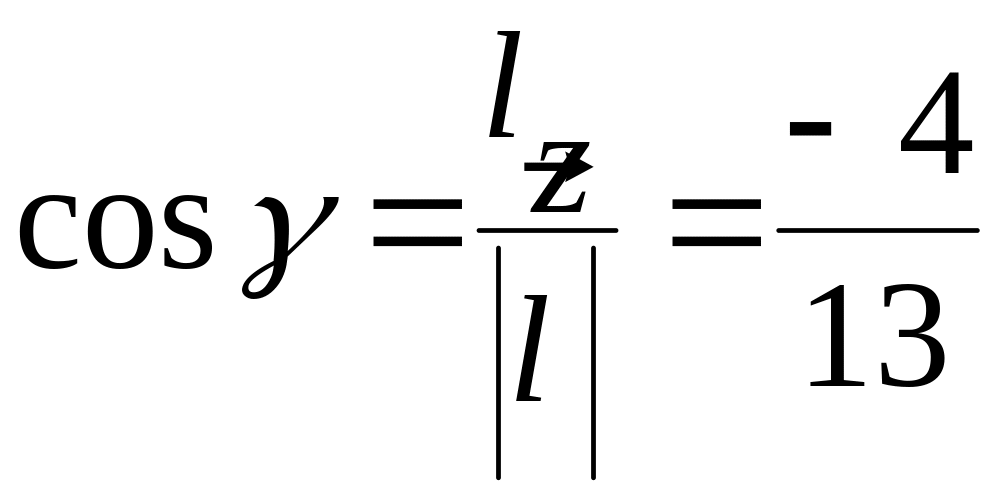 .
.
2) Подставляя в (1), найдем производную функции по указанному направлению в любой точке:
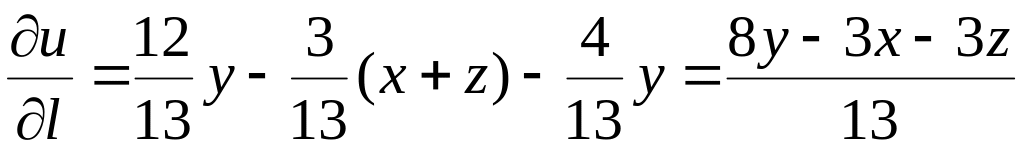 .
.
3) Подставляя координаты точек А и В, получим производные функции
 ,
,
 .
.
3.
Найти производную функции
![]() в точке
в точке
![]() в направлении, идущем от этой точки к
точке
в направлении, идущем от этой точки к
точке
![]() .
.
1) Находим частные производные функции и вычисляем их значения в точке Р:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
2)
найдем координаты вектора:
![]() ,
его модуль
,
его модуль
![]() и вычислим его направляющие косинусы:
и вычислим его направляющие косинусы:
 ,
,
 ,
,
![]() .
.
Отсюда
 .
.
Знак минус указывает, что в данном направлении функция убывает.
4.
Найти точки, в которых функция
![]() стационарна (т.е. точки, в которых
производная по любому направлению равна
нулю).
стационарна (т.е. точки, в которых
производная по любому направлению равна
нулю).
Для того чтобы в некоторой точке функция была стационарна, необходимо и достаточно, согласно формуле (1), чтобы в этой точке все ее частные производные первого порядка одновременно обращались в нуль.
Найдем частные производные первого порядка:
![]() и
и
![]() .
.
Решив
систему уравнений:
![]() и
и
![]() ,
получим 2 точки, в которых функция
стационарна:
,
получим 2 точки, в которых функция
стационарна:
![]() .и
.и
![]() .
.
