Геометрические приложения

10. Касательная плоскость и нормаль к поверхности. Особые точки

1. Пусть M и M₀ – точки данной поверхности. Проведем прямую MM₀. Плоскость, которая проходит через точку M₀, называется касательной плоскостью к поверхности, если угол между секущей MM₀ и этой плоскостью стремится к нулю, когда стремится к нулю расстояние MM₀.

Поверхность в своей произвольной точке имеет либо только одну касательную плоскость, либо не имеет ее вовсе.

Касательная плоскость к поверхности в точке M₀ содержит касательные прямые ко всем кривым, проведенным на поверхности через эту точку.

Пусть поверхность задана уравнением . Рассмотрим на ней точку . Будем предполагать, что , и одновременно не равны нулю. На поверхности через точку проведем всевозможные линии L и касательные прямые к этим линиям. Справедлива следующая теорема:

Теорема. Касательные прямые, проведенные к всевозможным линиям поверхности в точке , лежат в одной плоскости, называемой касательной плоскостью. Нормальный вектор касательной плоскости .

Доказательство.

2. Нормалью к поверхности в точке M₀ называется прямая, проходящая через точку касания M₀ перпендикулярно касательной плоскости к этой поверхности.

Нормальный вектор касательной плоскости одновременно является и направляющим вектором нормали.

Если поверхность задана уравнением , где – функция, дифференцируемая в точке , касательная плоскость в точке существует и имеет уравнение:

. (1)

Уравнение нормали к поверхности в этой точке:

(2)

Если поверхность задана уравнением и точка лежит на ней, то касательная плоскость к поверхности в точке определяется уравнением:

. (3)

Уравнение нормали к поверхности в этой точке:

. (4)

Равенство нулю в точке касания одной из частных производных, означает, что касательная параллельна той оси, по какой переменной частная обращается в нуль. Например, означает, что касательная плоскость параллельна оси Ох, а нормаль лежит в плоскости .

3. Точки поверхности , в которых одновременно обращаются в нуль все частные производные первого порядка , , , называют особыми. В таких точках поверхность не имеет ни касательной плоскости, ни нормали.

Особые точки плоской кривой (функция одной переменной). Обозначим значения частных производных в особой точке через: , и . Возможны три случая:

1) - через особую точку проходит 2 касательных, точка называется узлом.

2) - в особой точке нет касательных, точка называется изолированной.

3) - или изолированная точка, или точка возврата, или точка самосоприкосновения. В точках возврата и самосоприкосновения существует одна общая касательная к двум ветвям кривой. Чтобы в третьем, сомнительном случае решить вопрос однозначно, нужно узнать, имеются ли точки кривой в сколь угодно малой окрестности исследуемой точки

Примеры.

1. Найти уравнения касательной плоскости и нормали:

а) к поверхности в точке М(1, 1, 1).

Находим частные производные и их значения в указанной точке касания:

На основе формул (1) и (2) составим уравнения касательной и нормали.

Уравнение касательной плоскости:

Уравнение нормали:

б) к эллиптическому параболоиду в точке .

Преобразуем уравнение поверхности к виду: .

И, обозначив его левую часть через , найдем частные производные:

, , .

Вычислим их числовые значения в указанной точке :

, , .

Подставляя найденные значения в общие уравнения (3) и (4), получим

- уравнение касательной плоскости:

.

- уравнение нормали к поверхности в этой точке:

.

2. На сфере найти точки, где касательная параллельна плоскости .

1) Пользуясь общим уравнением (3), составим уравнение касательной плоскости к данной сфере в ее точке (координаты которой нам нужно найти):

, , - частные производные уравнения сферы.

, , - их значения в точке касания. Отсюда:

Сократив выражение на 2, и раскрыв скобки, получим:

или .

2) Точка сферы должна удовлетворять ее уравнению . Это означает, что . Следовательно,

.

3) Воспользуемся условием параллельности искомой касательной к заданной плоскости. Согласно условию параллельности двух плоскостей, коэффициенты при текущих координатах этих плоскостей должны быть пропорциональны:

.

Запишем последние равенства в виде системы уравнений:

(*)

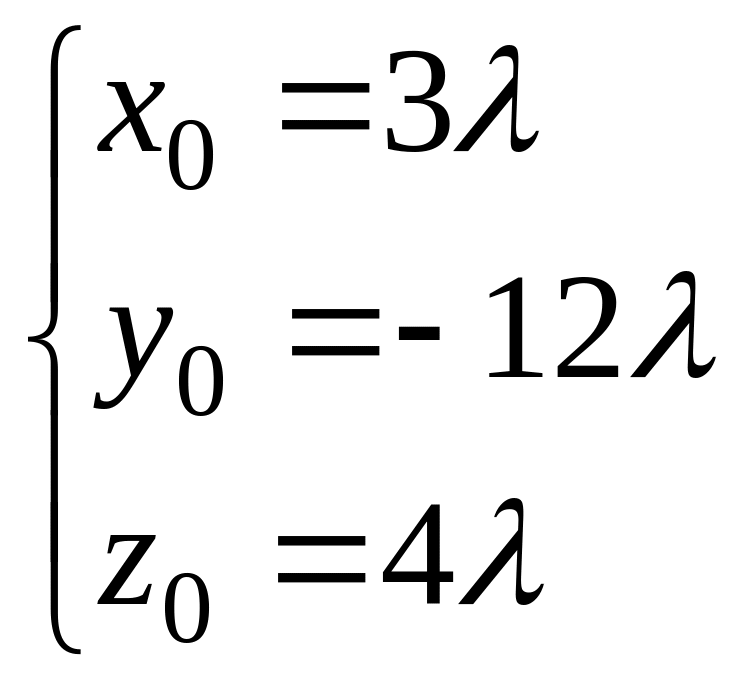4) Подставим найденные в параметрическом виде (*) координаты точек сферы в ее уравнение:

,

откуда находим, что .

5) Подставляя найденные числовые значения в (*), найдем координаты искомых точек, в которых касательная плоскость параллельна заданной плоскости:

и .

3. Показать, что касательные плоскости к поверхности образуют с координатными плоскостями тетраэдр постоянного объема.

Уравнение касательной плоскости к данной поверхности в точке имеет вид:

.

Эта плоскость на координатных осях отсекает отрезки:

, , .

Перечисленные отрезки являются взаимно перпендикулярными ребрами тетраэдра, образованного касательной плоскостью и координатными плоскостями. Приняв одно из этих ребер за высоту тетраэдра, найдем, что его объем

, так как точка лежит на данной поверхности. Причем объем не зависит от координат точки касания. Из этого следует, что различные касательные плоскости к данной поверхности образуют с плоскостями координат тетраэдр постоянного, равного, объема.