5. Написать уравнение плоскости, инвариантной относительно линейного преобразования , заданного в некотором ортонормированном базисе матрицей
6. Пусть Г – матрица Грама некоторого базиса и А – матрица линейного преобразования . Найти матрицу А1 сопряженного преобразования * в том же базисе:
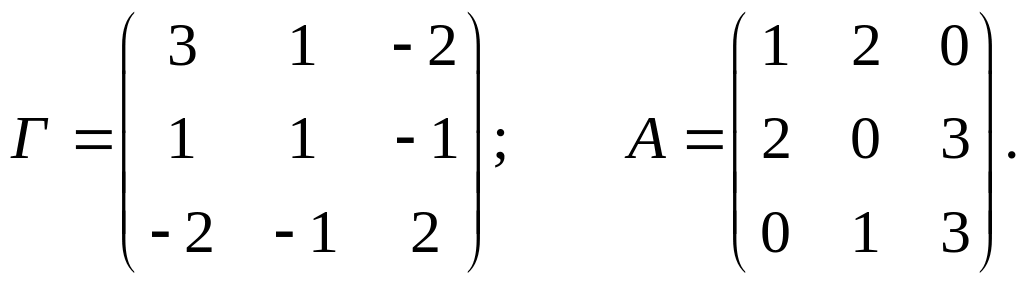
7.Доказать, что если линейное преобразование в n-мерном пространстве имеет n различных собственных значений, то любое линейное преобразование, перестановочное с , имеет базис, состоящий из его собственных векторов.
8. Доказать, что подпространство V, состоящее из всех собственных векторов преобразования с собственными значениями и нулевого вектора, инвариантно относительно любого линейного преобразования , перестановочного с .
9. Доказать, что если х – собственный вектор нормального преобразования евклидова пространства, принадлежащий собственному значению , то х является собственным вектором для сопряженного преобразования *, принадлежащим тому же самому числу .
10. Доказать, что собственные векторы нормального преобразования, принадлежащие различным собственным значениям, ортогональны.
11. Пусть нормальное преобразование в евклидовом пространстве Е, причем 2 = . Доказать, что * = . ( тождественное преобразование).
12. Пусть р(t) = t2 + at + b – вещественный неприводимый многочлен. Предположим, что нормальное преобразование в евклидовом пространстве, причем р() = 0. Доказать, что * = а.
13. Пусть нормальное линейное преобразование в двумерном евклидовом пространстве Е, причем не имеет собственных векторов в этом пространстве. Пусть е = (е1, е2) – ортонормированный базис. Доказать, что матрица преобразования в базисе е имеет вид:
14. Доказать, что если подпространство L унитарного пространства инвариантно относительно линейного преобразования , то ортогональное дополнение L* инвариантно относительно сопряженного преобразования *.
15. Доказать, что линейное преобразование унитарного пространства Rn имеет инвариантное подпространство любого числа измерений от 0 до n.
16. Пусть е1, е2 – ортонормированный базис в унитарном пространстве Е2, f1 = e1 + e2, f2 = e1 ie2. Линейное преобразование , действующее в этом пространстве, имеет в базисе f1, f2 матрицу
А
=
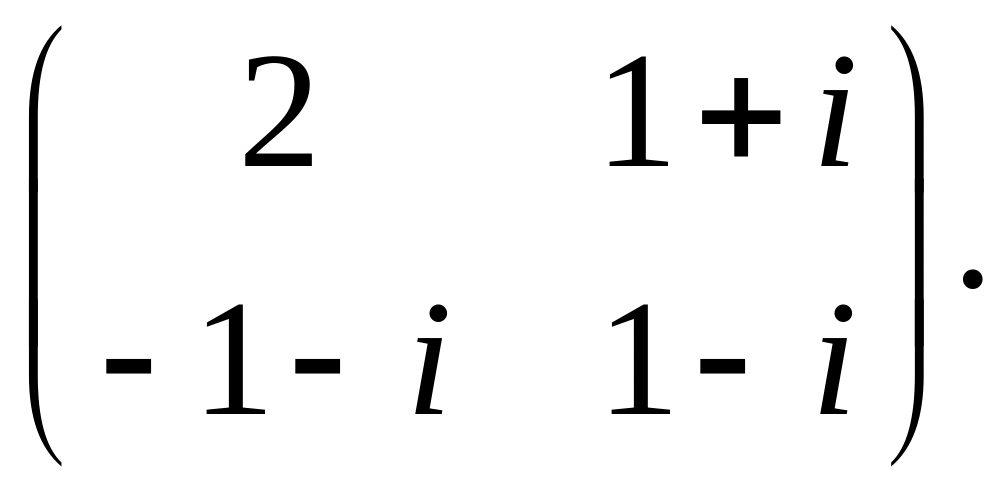
Найти матрицу сопряженного преобразования * в базисе f1, f2.
17. Пусть е1 ,е2, е3 – ортонормированный базис в унитарном пространстве Е3, f1 = e1, f2 = ie1 + e2, f3 = ie1 + e2 + e3. Линейное преобразование , действующее в этом пространстве, имеет в базисе f1, f2, f3 матрицу
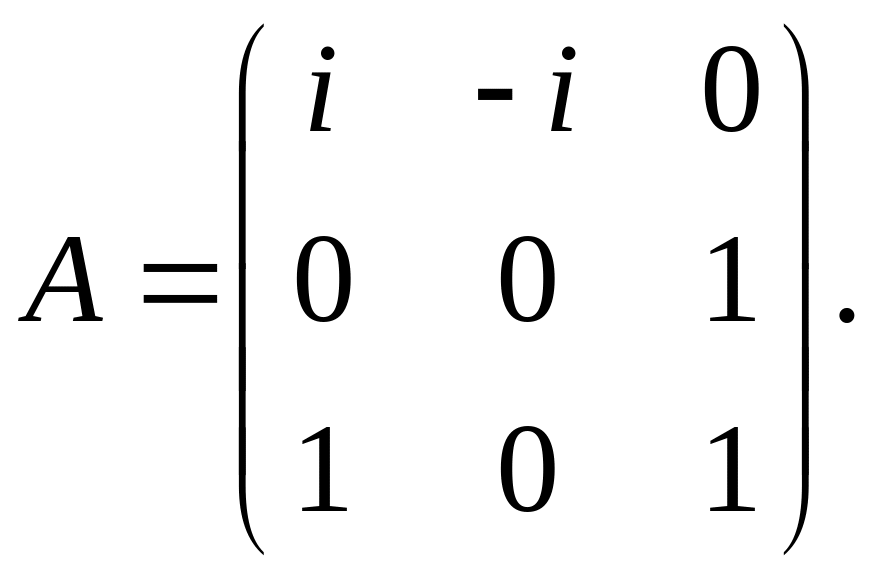
Найти матрицу сопряженного преобразования в базисе f1, f2, f3.
18. Доказать, что коэффициенты характеристического многочлена преобразования , действующего в унитарном пространстве, являются комплексно сопряженными по отношению к соответствующим коэффициентам характеристического многочлена сопряженного преобразования *.
19. Проверить, что самосопряженные, унитарные и эрмитовы преобразования унитарных пространств нормальны.
20. Доказать, что нормальное преобразование унитарного пространства тогда и только тогда является самосопряженным, когда все его собственные значения вещественны.
21. Доказать, что если х – собственный
вектор нормального преобразования
унитарного пространства, принадлежащий
собственному значению ,
то х является собственным вектором для
сопряженного преобразования *,
принадлежащим сопряженному числу
.
22. Доказать, что собственные векторы нормального преобразования, принадлежащие двум различным собственным значениям, ортогональны.
23. Пусть е – собственный вектор нормального преобразования . Доказать, что подпространство L, состоящее из всех векторов пространства, ортогональных е, инвариантно относительно .
24. Доказать, что для нормальности линейного преобразования унитарного пространства необходимо и достаточно, чтобы каждый собственный вектор был собственным и для *.
25. Доказать, что если нормальное преобразование в унитарном пространстве перестановочно с преобразованием , то перестановочно с *.
26. Пусть и нормальные преобразования в унитарном пространстве, причем характеристические многочлены этих преобразований равны. Доказать, что матрицы преобразований и в любом базисе подобны.
27. Пусть нормальное нильпотентное преобразование в унитарном пространстве. Доказать, что тогда = 0.