Ответы.

1. Нет.

2. 2. А) 1) Нет. 2) Да. 3) Да.

Б) В случае 2): (Х,У) = 2,

В случае 3) (Х, У) = 0,

3. В случае 2)

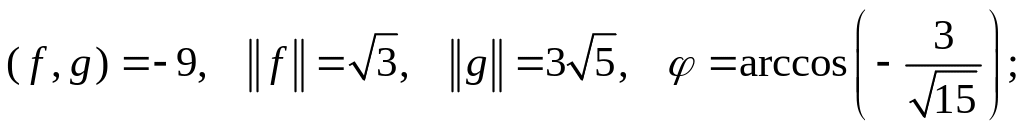
В случае 3)

4. 9.

5. Да, если  = 0, нет, если   0.

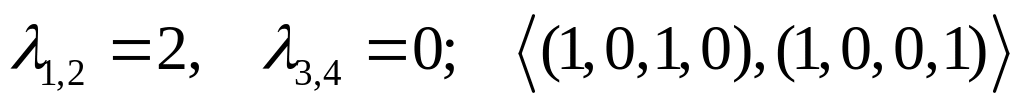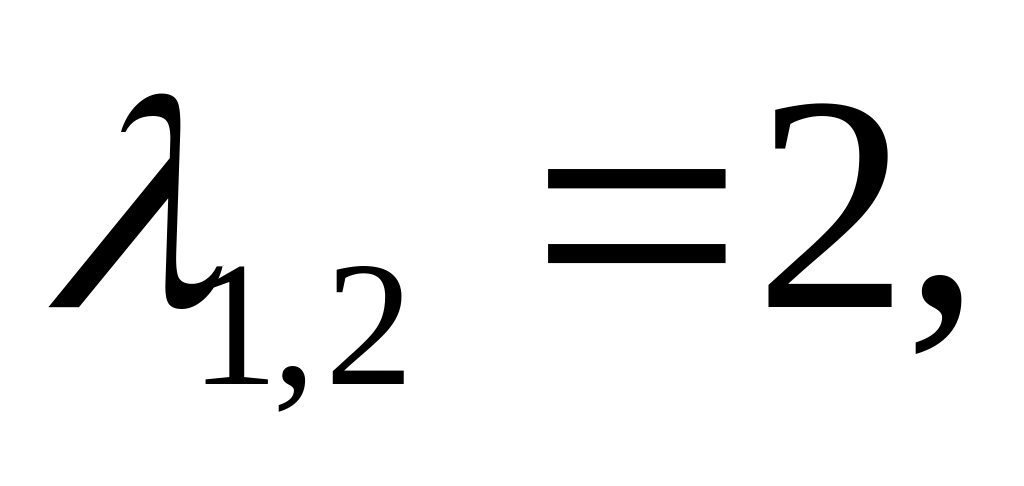
11. для

для

Задание № 274.

1.Доказать, что а)если (х, у) = 0 для любого элемента х, то у = 0;

б)если (х, у) = (х, z) для любого элемента х ( y, z  фиксированные элементы, то y = z.

2.Найти нормированный вектор, ортогональный к векторам

a₁ = (1, 1, 1, 1), a₂ = (1, 1, 1, 1), a₃ = (2, 1, 1, 3).

3.Определить косинусы углов между прямой х₁ = х₂ = ... = х_n и осями координат.

4.Проверить, что векторы следующей системы попарно ортогональны и дополнить ее до ортогонального базиса: а = (1, 2, 2, 3), b =(2, 3, 2, 4).

5.Применяя процесс ортогонализации, найдите ортогональный базис

пространства, натянутого на данную систему векторов:

a) a₁ = (1, 0, 1, 0), a₂ = (1, 2, 3, 4);

b) a₁ = (1, 1, 1, 2), a₂ = (5, 8, 2, 3), a₃ = (3, 9, 3, 8).

6.Найти угол между вектором х и линейной оболочкой  < а_i >:

x = (2, 2, 1, 1), a₁ = (3, 4, 4, 1), a₂ = (0, 1, 1, 2).

7.Применить процедуру ортогонализации к элементам х₁, х₂, х₃ евклидова пространства, если:

а) х₁ = е₁  2е₂ + 2е₃, х₂ = е₁  е₃, х₃ = 5е₁ 3е₂ 7е₃, где е₁ ,е₂, е₃  ортонормированный базис евклидова пространства;

б) х₁ = е₁ + е₂ + е₃ + е₄, х₂ = 3е₁ +3е₂  е₃  е₄; х₃ = 2е₁ + 6е₃ + 8е₄, где е₁ ,е₂, е₃, е₄  ортонормированный базис евклидова пространства.

8. Пусть L₁ и L₂  линейные подпространства евклидова (или унитарного) пространства Rⁿ, причем размерность L₁ меньше размерности L₂; доказать, что в L₂ найдется ненулевой вектор, ортогональный ко всем векторам из L₁.

9.Применяя процесс ортогонализации, построить ортогональный базис оболочек векторов:

1. <(1, 2, 2, 1), (1, 1, 5, 3), (3, 2, 8, 7)>;

2. <(1, 1, 1, 2), (5, 8, 2, 3), (3, 9, 3 8)>;

3. <(2, 1, 3 1), (7, 4, 3, 3), (1, 1, 6, 0), (5, 7, 7, 8)>.

10. Доказать, что если линейно независимые векторы а₁, а₂,…, а_n процессом ортогонализации переводятся в векторы b₁, b₂,…, b_n , то

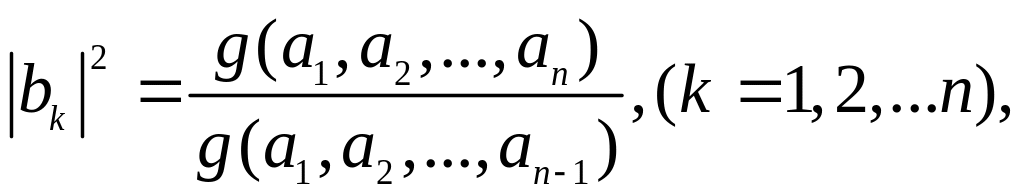
здесь g(а₁, а₂,…)  определители Грама. Определитель Грама с нулевым числом векторов принимается равным единице.

Ответы.

1. Доказательство. 5а. (1, 0, 1, 0), (1, 2, 1, 4).

5б. (1, 1, 1, 2), (2, 5, 1, 3).

2. (0, , , 0). 6. 60⁰.

3. cos 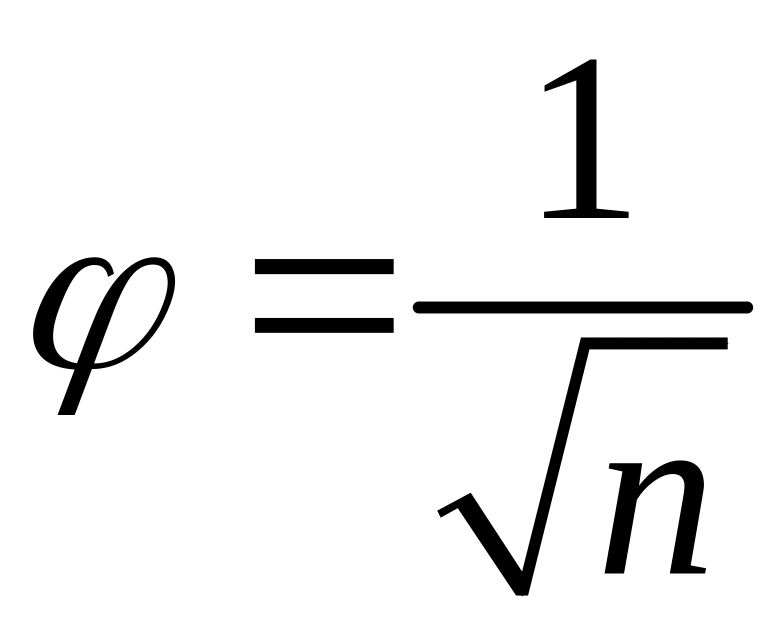 . 7. а) е₁  2е₂ + 2е₃, 2е₁ + 2е₂ + е₃,

6е₁  3е₂ 6е₃;

б) е₁ + е₂ + е₃ + е₄, 2е₁ + 2е₂  2е₃  2е₄,

е₁ + е₂  е₃ + е₄.

4. (2, 2, 1, 0), (5, 2, 6, 1).

9. a) (1, 2, 2, 1), (2, 3, 3, 2), (2, 1, 1, 2); b) (1, 1, 1, 2), (2, 5, 1, 3);

c) (2, 1, 3, 1), (3, 2, 3, 1), (1, 5, 1, 10).

28. Задачи для самостоятельного решения

1. Пусть е₁, е₂ – ортонормированный базис плоскости и линейное преобразование  в базисе f₁ = e₁, f₂ = e₁+e₂ имеет матрицу .

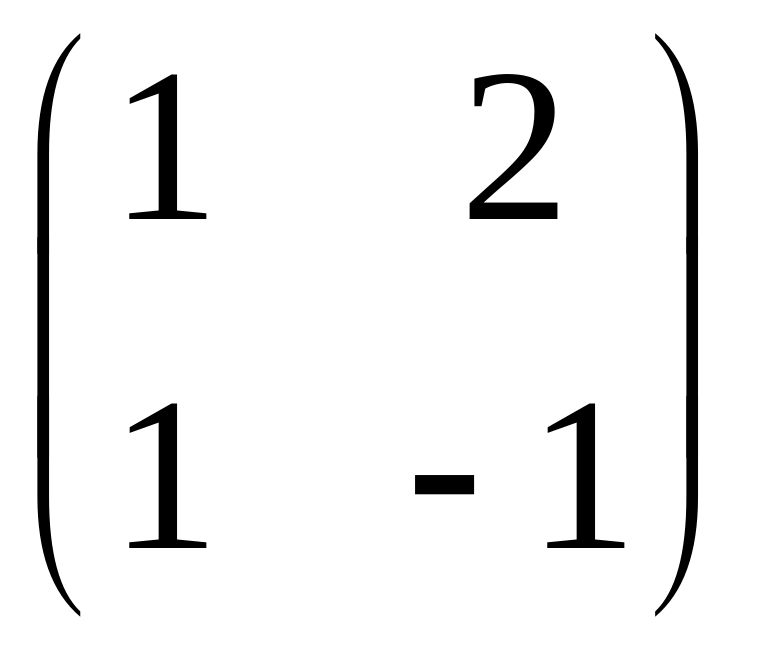Найти матрицу сопряженного преобразования в том же базисе f₁, f₂.

2. Найти матрицу линейного преобразования *, сопряженного преобразованию  в ортонормированном базисе е₁, е₂, е₃, если  переводит векторы а₁ = (0,0,1), а₂ = (0,1,1), а₃ = (1,1,1) в векторы b₁ = (1,2,1), b₂ = (3,1,2), b₃ = (7,1,4) соответственно, где координаты всех векторов даны в базисе е₁, е₂, е₃.

3. Пусть хОу – прямоугольная система координат на плоскости и   проектирование плоскости на ось Ох параллельно биссектрисе первой и третьей четверти. Найти сопряженное преобразование *.

4. Пусть =  разложение евклидова пространства в прямую сумму двух подпространств;   проектирование Rⁿ на L₁ параллельно L₂ ; L₁* и L₂*  ортогональные дополнения соответственно для L₁ и L₂ ; *  преобразование, сопряженное с . Доказать, что Rⁿ = и что * является проектированием Rⁿ на L₂* параллельно L₁*.