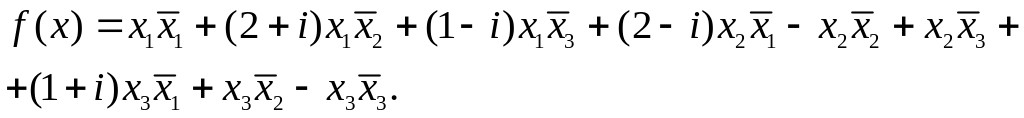- •7. Вычислить выражения:
- •Вычислить:
- •Задание № 4-3.
- •Задание 5-4.
- •3. Вычислить определители:
- •Задание 6-3.
- •Задание № 73.
- •Задание № 8-5.
- •Задание 9-2.
- •2.Вычислить выражения:
- •Задание 101.
- •Ответы.
- •Задание № 13 1.
- •Ответы.
- •Задание № 143.
- •Ответы.
- •Задание № 15 4.
- •Ответы .
- •Задание № 16-2.
- •Ответы.
- •Задание № 17-1.
- •Задание № 18-5.
- •Ответы.
- •Задание № 19-4 .
- •Задание № 22-1.
- •Ответы.
- •Задание № 23 2.
- •Ответы.
- •Задание 243.
- •Ответы.
- •5. Доказательство.
- •25. Задания для самостоятельной работы.
- •Ответы.
- •26. Задачи и упражнения для самостоятельной работы
- •Ответы.
- •Задание № 274.
- •9.Применяя процесс ортогонализации, построить ортогональный базис оболочек векторов:
- •28. Задачи для самостоятельного решения
- •5. Написать уравнение плоскости, инвариантной относительно линейного преобразования , заданного в некотором ортонормированном базисе матрицей
- •9. Ответы к задачам для самостоятельного решения
- •29. Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •30. Задачи для самостоятельного решения.
- •Ответы к задачам для самостоятельного решения.
9. Ответы к задачам для самостоятельного решения
1.
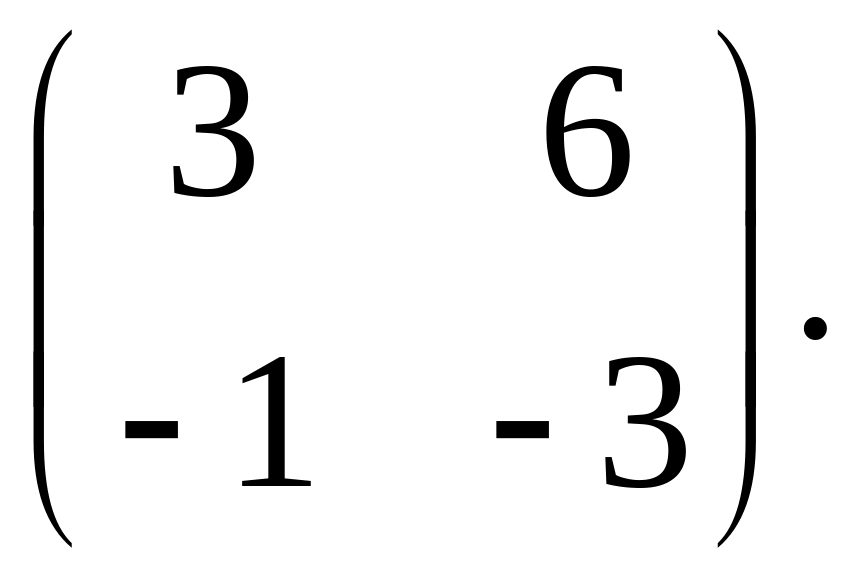
2.
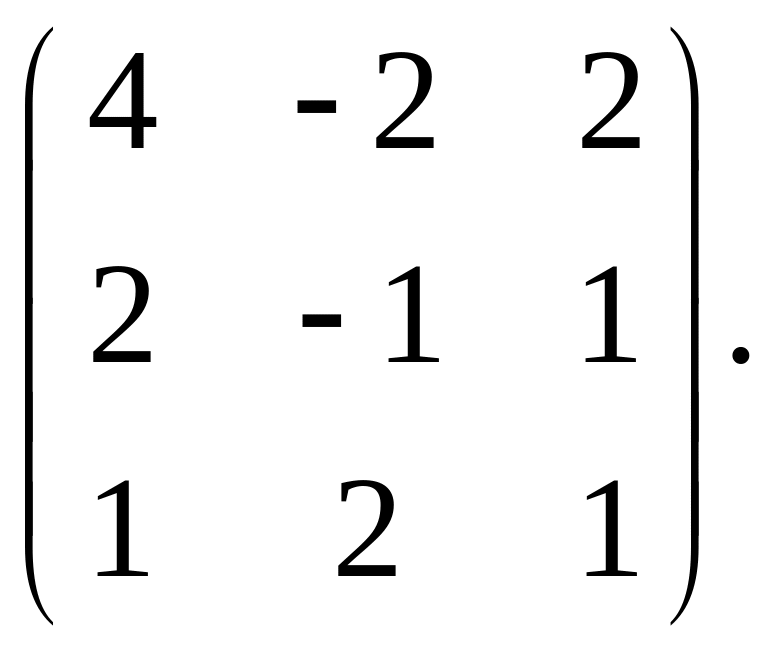
3. * – проектирование на биссектрису 2-й и 4-й четверти параллельно оси Оу.
4. Указание: Показать, что если z L1, и L2, то *(z) = 0, *(u) = u.
5. 3x1 3x2 + x3 = 0.
6.
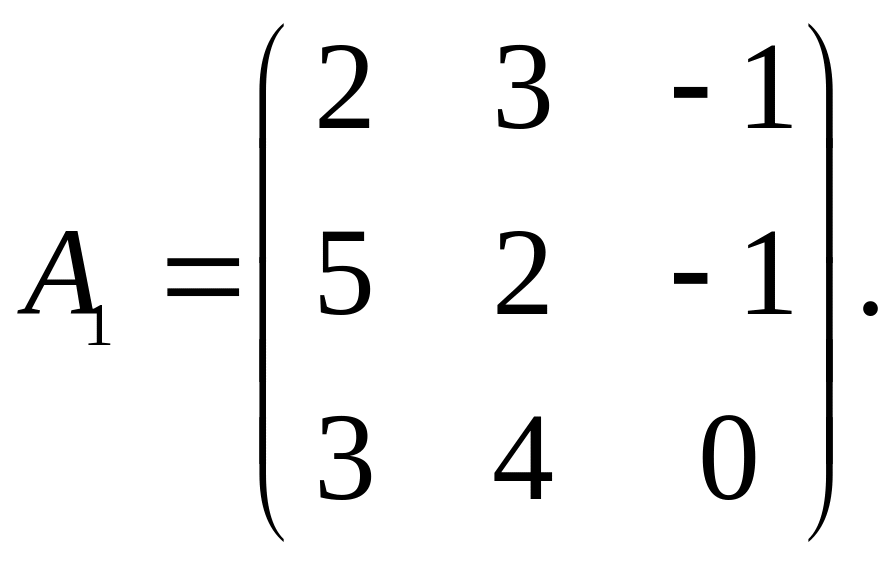
9. Указание: доказать равенство:
((х) х, (х) х) = ( *(х) х, *(х) х).
14. Указание: Показать, что ортогональное дополнение к одномерному подпространству, инвариантному относительно сопряженного преобразования *, инвариантно относительно .
16.
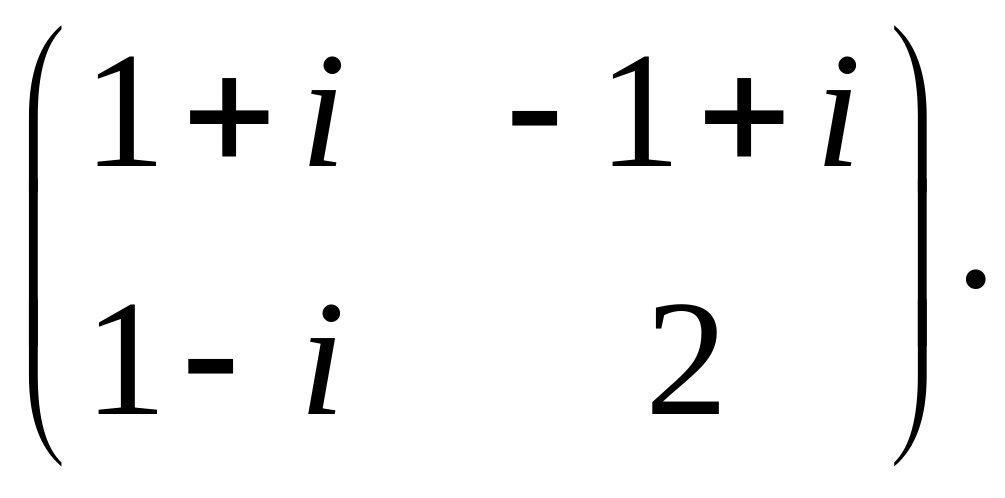
17.
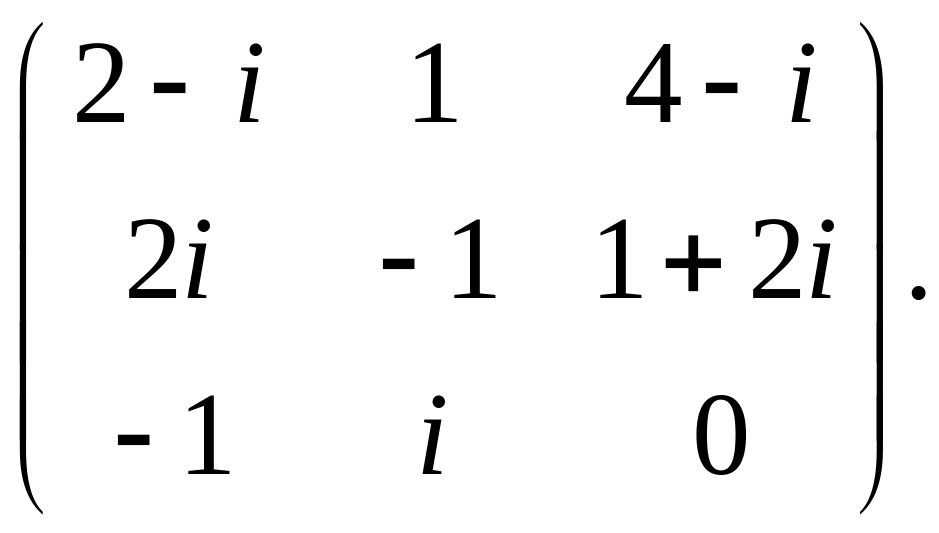
21.
Указание: Доказать равенство:
![]()
29. Задачи для самостоятельного решения
47. Доказать, что линейная комбинация самосопряженных преобразований с вещественными коэффициентами (в частности, сумма двух самосопряженных преобразований) есть самосопряженное преобразование.
48. Доказать, что произведение двух самосопряженных преобразований и тогда и только тогда будет самосопряженным, когда и перестановочны.
49. Доказать, что проектирование евклидова пространства Rn на подпространство L1 параллельно подпространству L2 тогда и только тогда будет самосопряженным линейным преобразованием, когда L1 и L2 ортогональны.
50. Найти ортонормированный базис собственных векторов и матрицу В в этом базисе для линейного преобразования , заданного в некотором ортонормированном базисе матрицей А:
а)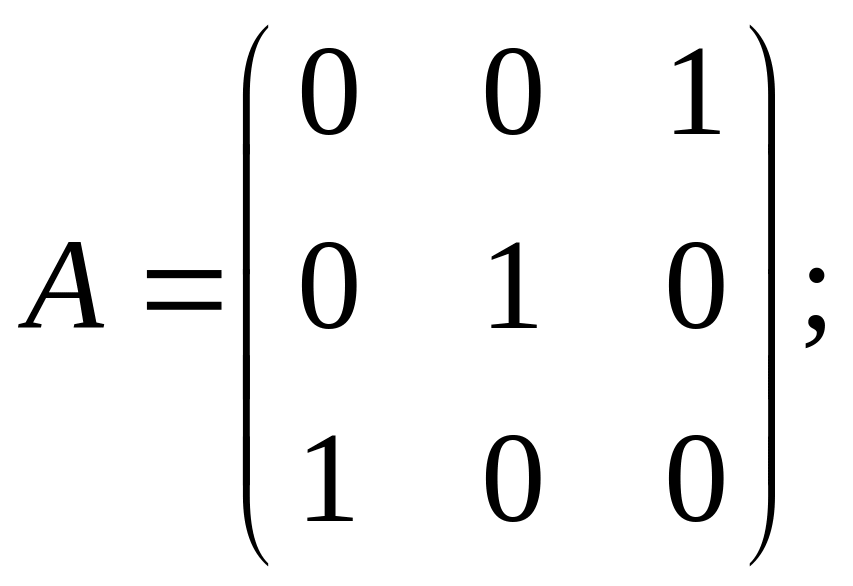 б)
б)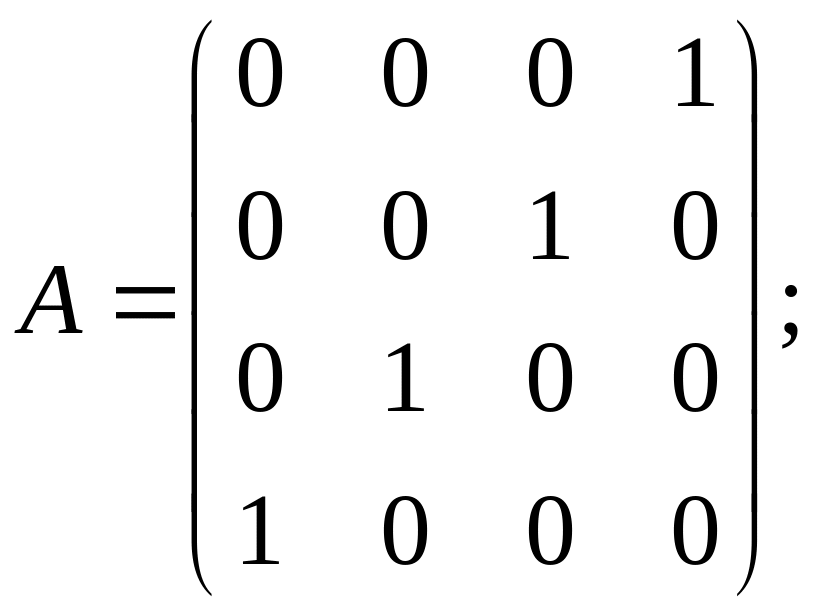 в)
в)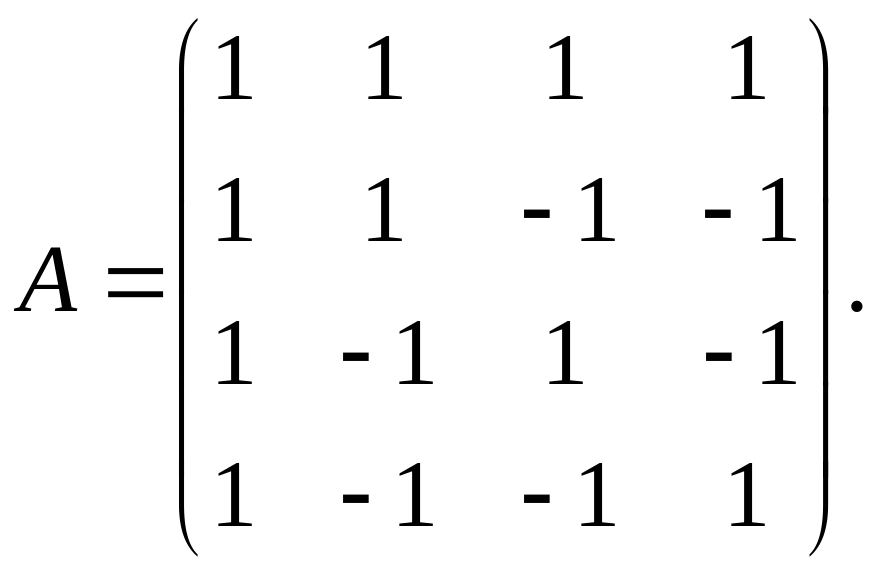
51. Доказать, что если и самосопряженные преобразования, то преобразование + также самосопряжено.
72. Доказать, что линейное преобразование унитарного пространства тогда и только тогда является нормальным, когда = , где самосопряженное и унитарное преобразования, перестановочные между собой.
73. Доказать, что:
а) каждое линейное преобразование унитарного пространства однозначно представляется в виде = 1 + i2, где 1 и 2 – эрмитовы преобразования;
б) для того чтобы преобразование было нормальным, необходимо и достаточно, чтобы преобразования 1 и 2 в вышеуказанном представлении были перестановочны.
74. Доказать, что если и эрмитовы преобразования, то эрмитовыми будут также преобразования + и i( ).
75. Найти ортонормированный базис из собственных векторов эрмитова преобразования, заданного в некотором ортонормированном базисе матрицей:
а)
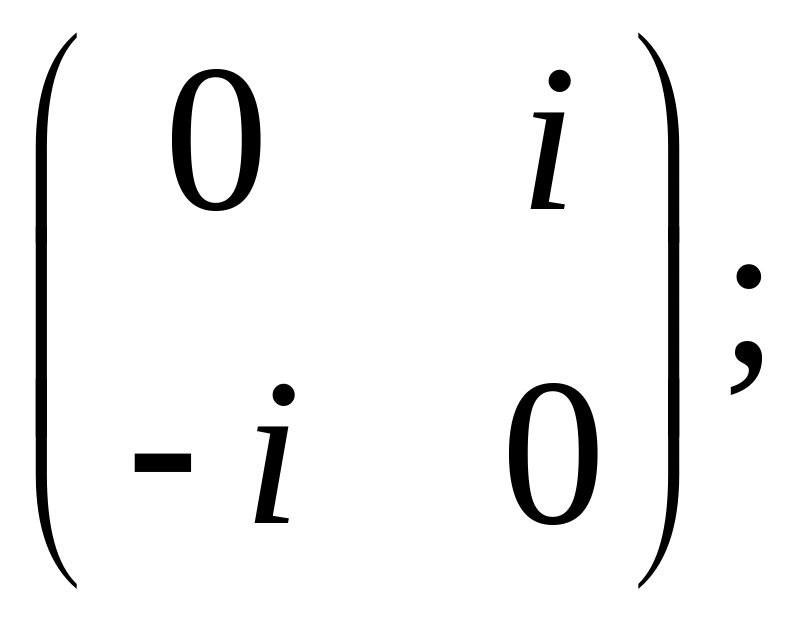 б)
б)
 в)
в)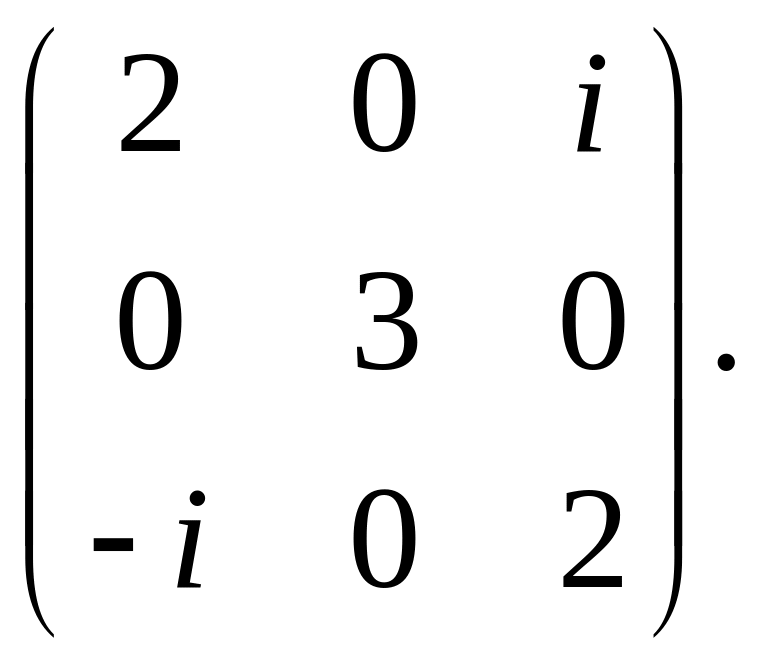
76. В некотором ортонормированном базисе эрмитово преобразование задано матрицей А. Найти базис из собственных векторов преобразования, диагональную матрицу В преобразования в в этом базисе и унитарную матрицу С такие, что В = С1АС:
а)
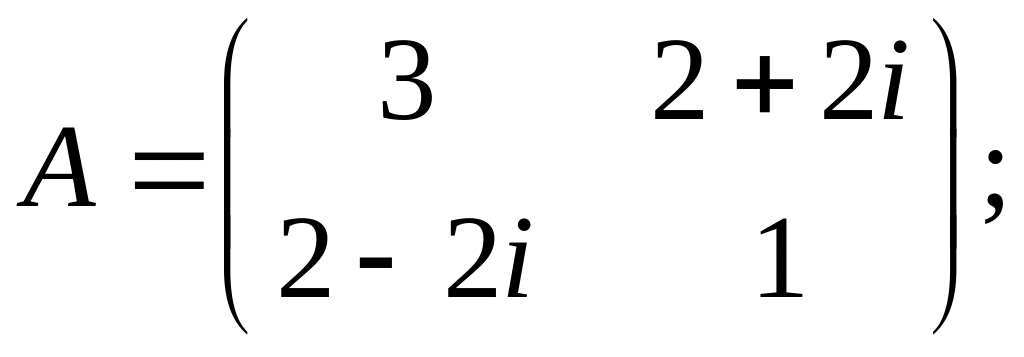 б)
б)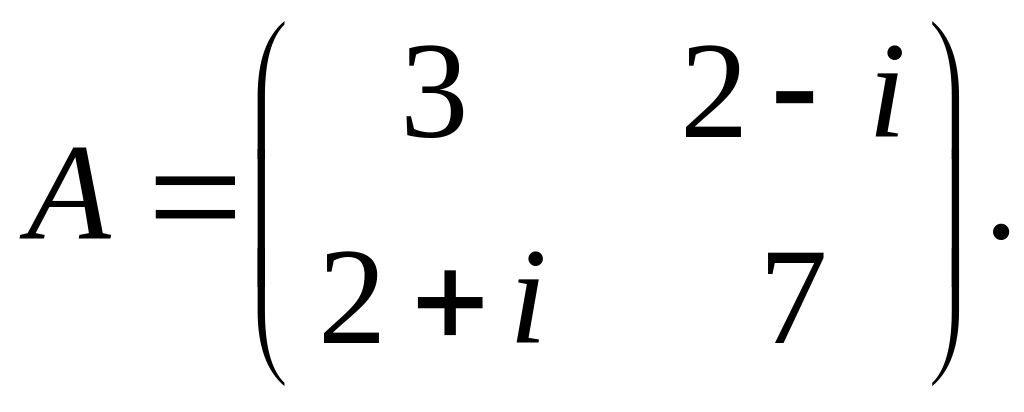
Ответы к задачам для самостоятельного решения
50. а)
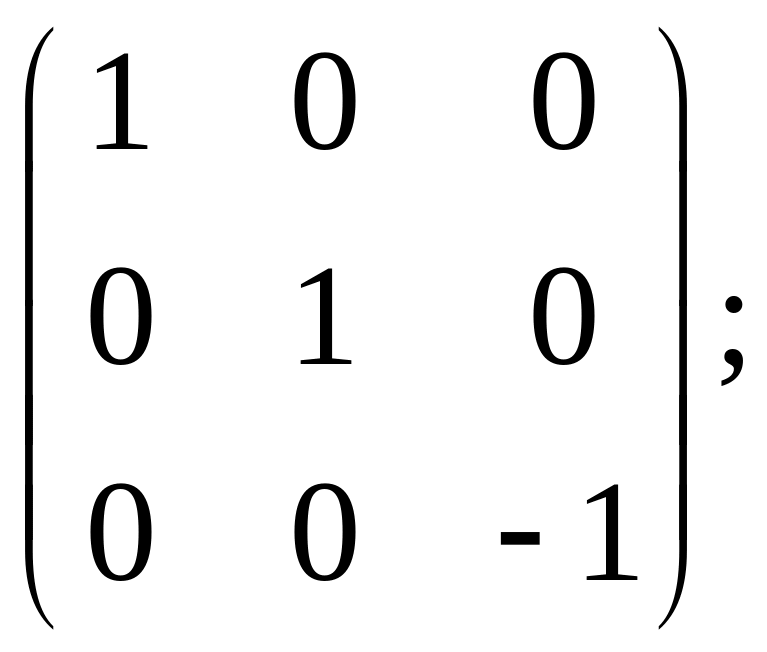
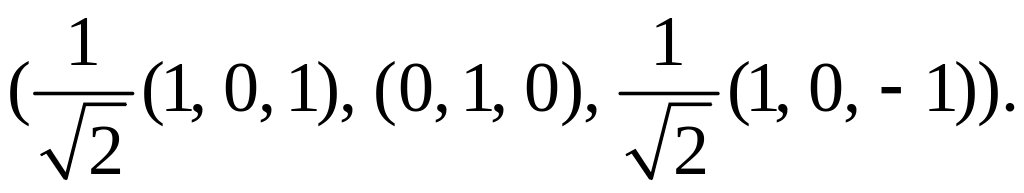
b)
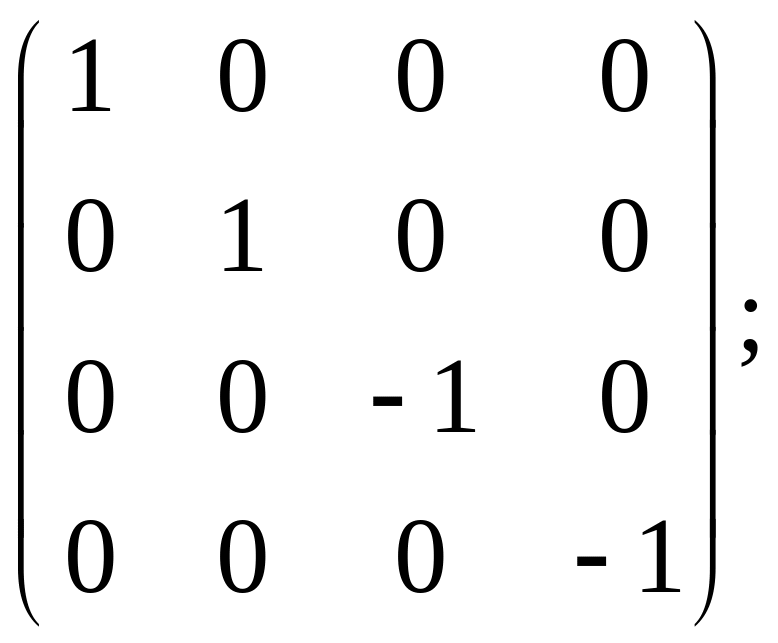
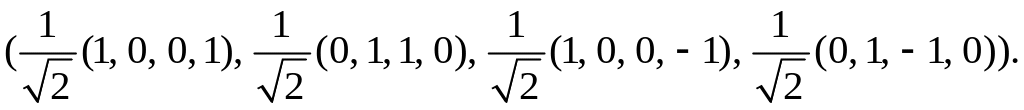
c)
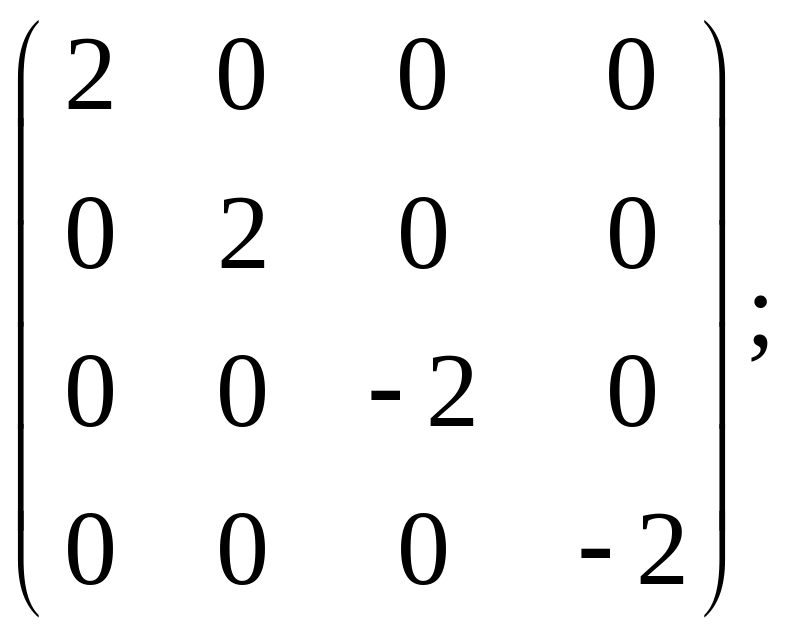
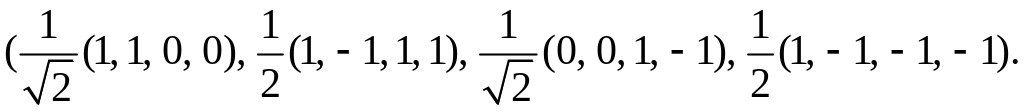
76. а)
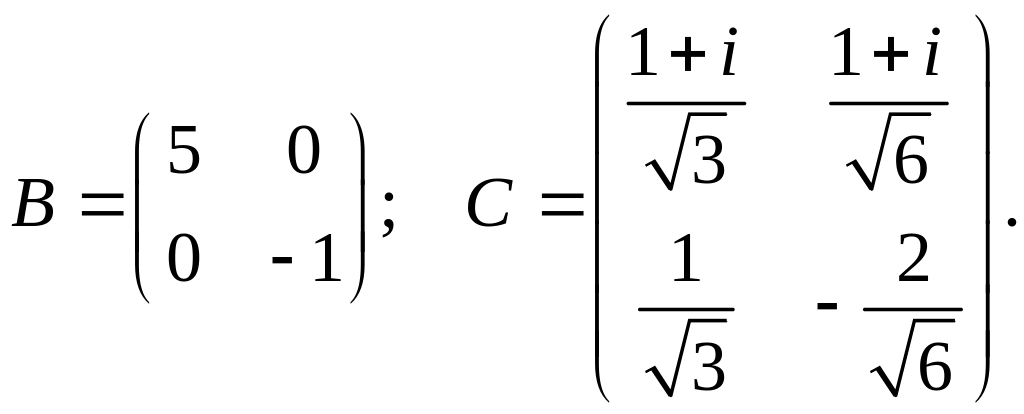
б)
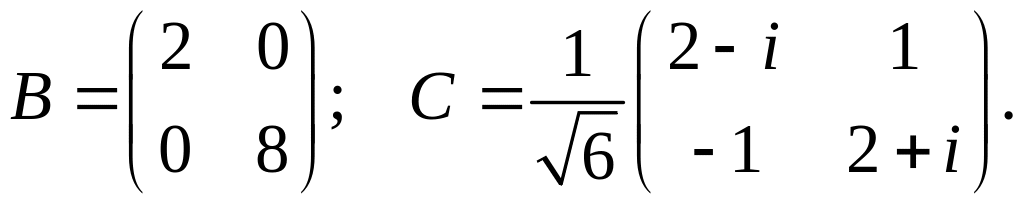
30. Задачи для самостоятельного решения.
1. Являются ли билинейными формами следующие функции от двух систем переменных:
f(x, y) =
 ,
,
где Х,Y – столбцы вещественных чисел высотой n;
f(x, y) = tr(XY-YX),
где Х,YMn(R), trA – след матрицы А;
f(x, y) = det(XY), X,Y Mn(R);
f(x, y) = tr(A + B);
f(x, y) = tr(A
 );
);f(x, y) = tr(
 );
);f(x, y) =
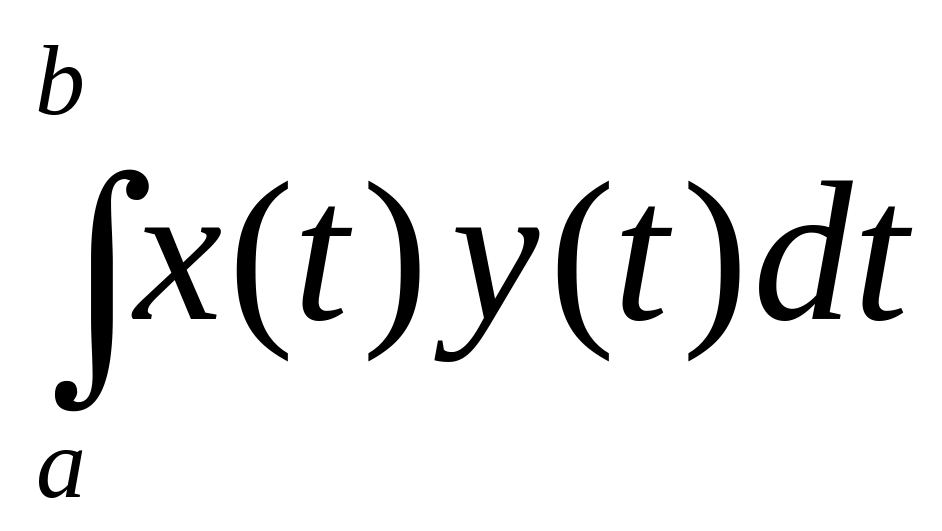 ,
,
где
![]() – непрерывные функции на отрезке [a,
b];
– непрерывные функции на отрезке [a,
b];
f(x, y) =
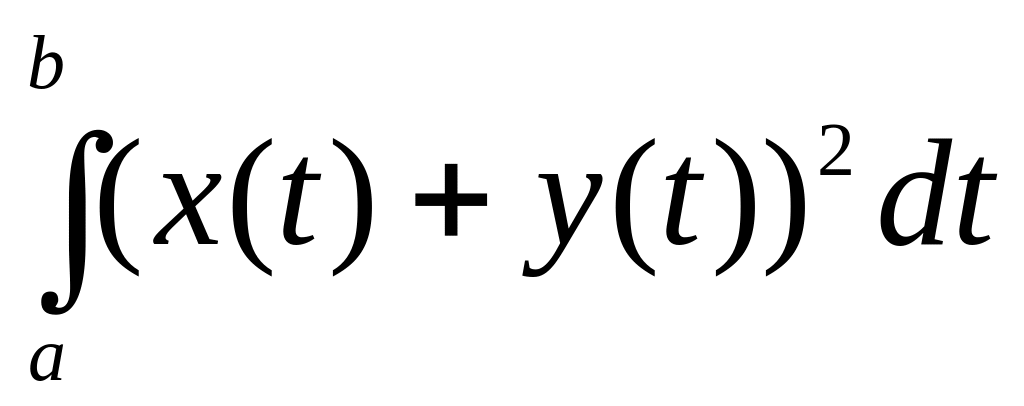 ,
,
где – непрерывные функции на отрезке [a, b];
f(x, y) = (x, y),
где (x, y) – скалярное произведение векторов х, у Rn .
2. Найти матрицу билинейной формы f(x, y) в новом базисе если заданы ее матрица А в старом базисе и формулы перехода к новому базису:
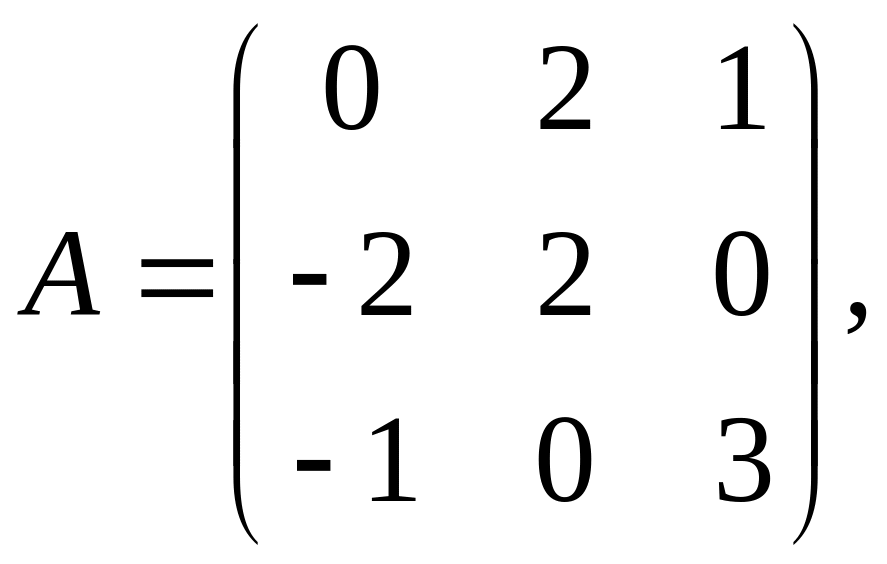
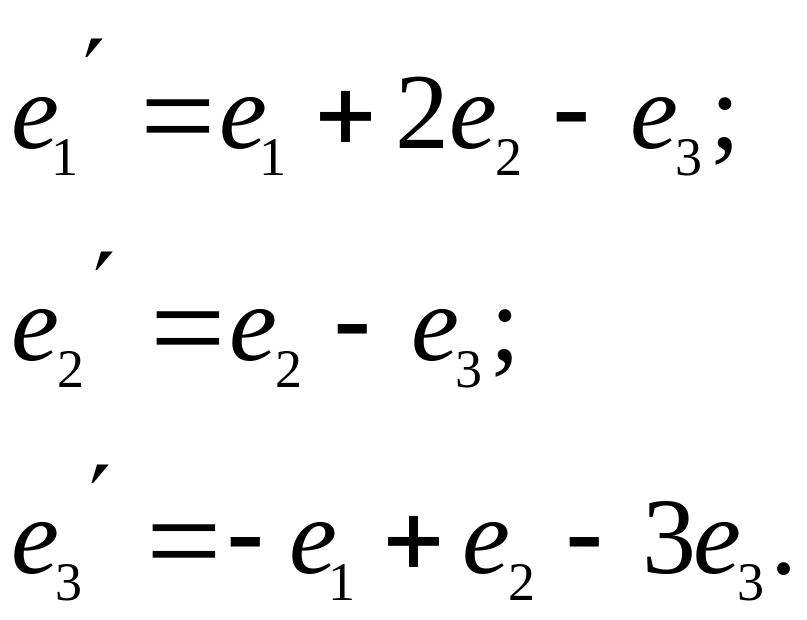
3. Привести к нормальному виду следующие симметрические билинейные формы, найти матрицы перехода:
f(x, y) = x1y1 + x1y2 + x2y1 + 2x2y2 + 2x2y3 + 2x3y2 + 5x3y3;
f(x, y) = x1y1 + 0,5x1y2 + 0,5x2y1 + 0,5x3y4 + 0,5x4y3;
f(x, y) = x1y1 2x1y2 + x1y3 2x2y1 + 4x2y2 + x3y1 x3y3.
4. Привести к каноническому виду следующие симметрические билинейные формы, найти ортогональные матрицы перехода:
f(x, y) =
 (2x1y1
+
2x1y2
+
2x2y1
x2y2
+
2x2y3
2x3y1
+
2x3y2
+
+2x3y3);
(2x1y1
+
2x1y2
+
2x2y1
x2y2
+
2x2y3
2x3y1
+
2x3y2
+
+2x3y3);f(x, y) = 17x1y1 8x1y2 + 4x1y3 8x2y1 + 17x2y2 4x2y3 + 4x3y1
4x3y2 + 11x3y3;
f(x, y) = 11x1y1 + 2x1y2 8x1y3 + 2x2y1 + 2x2y2 + 10x2y3
8x3y1 + 10x3y2 + 5x3y3;
f(x, y) = 2x1y1 2x1y2 + x2y2 2x2y3 2x3y2.
5. Записать квадратичные формы в матричном виде:
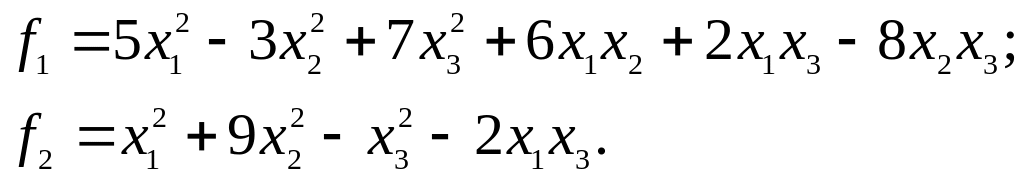
6.
Записать квадратичные формы
![]() по их матрицам:
по их матрицам:

7. При каких значениях следующие квадратичные формы являются положительно определенными:
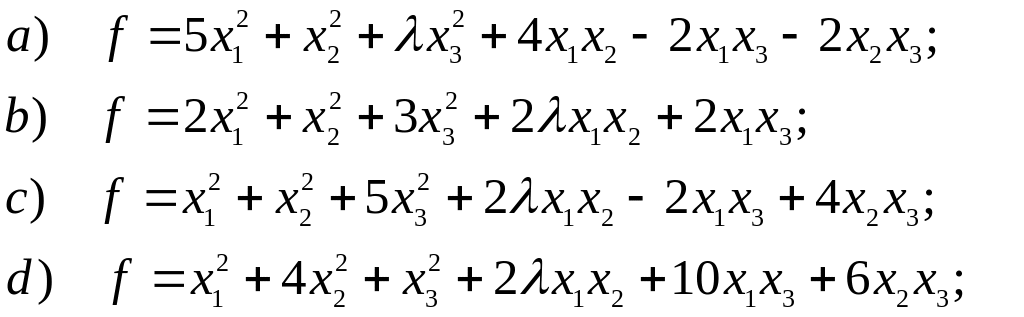
8. Методом Лагранжа привести квадратичную форму к нормальному виду (к сумме квадратов) и найти соответствующее невырожденное преобразование переменных.
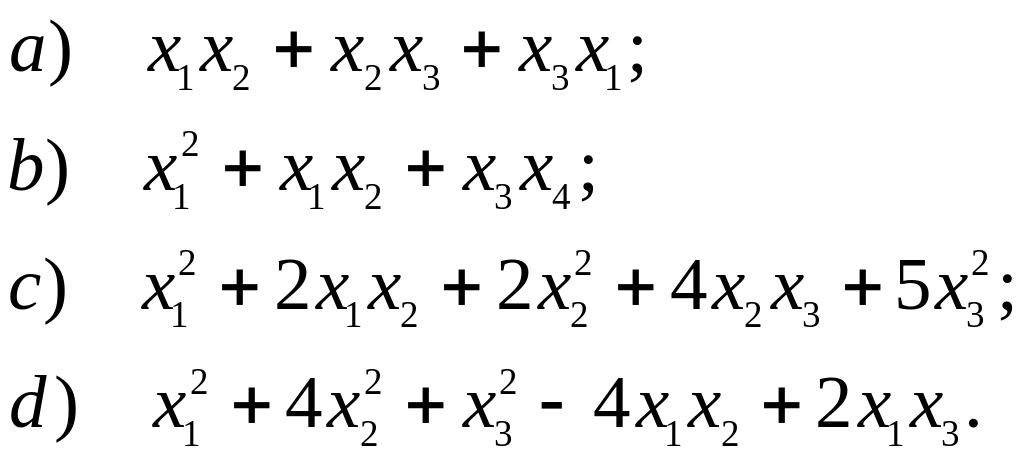
9. Привести к каноническому виду квадратичные формы и найти соответствующие ортогональные преобразования переменных.
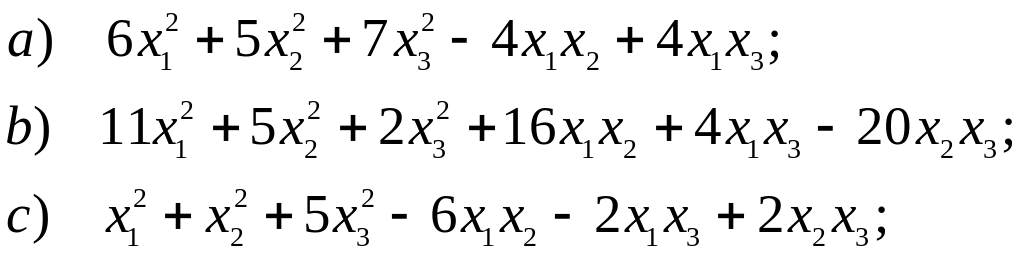
![]()
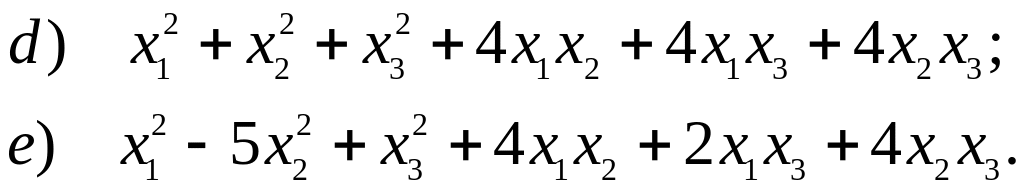
10. Для следующих форм найти невырожденное линейное преобразование, переводящее форму f(x) в форму g(y) (искомое преобразование определяется неоднозначно).
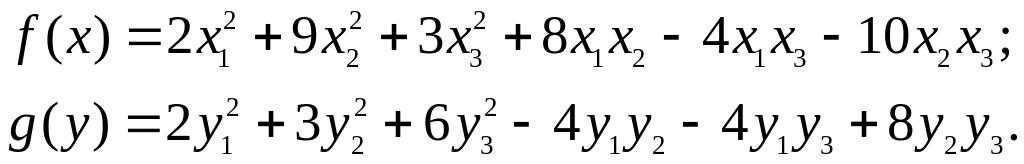
11. Найти невырожденное линейное преобразование, приводящее одну из форм (положительно определенную) следующих пар квадратичных форм к нормальному, а другую форму той же пары к каноническому виду.
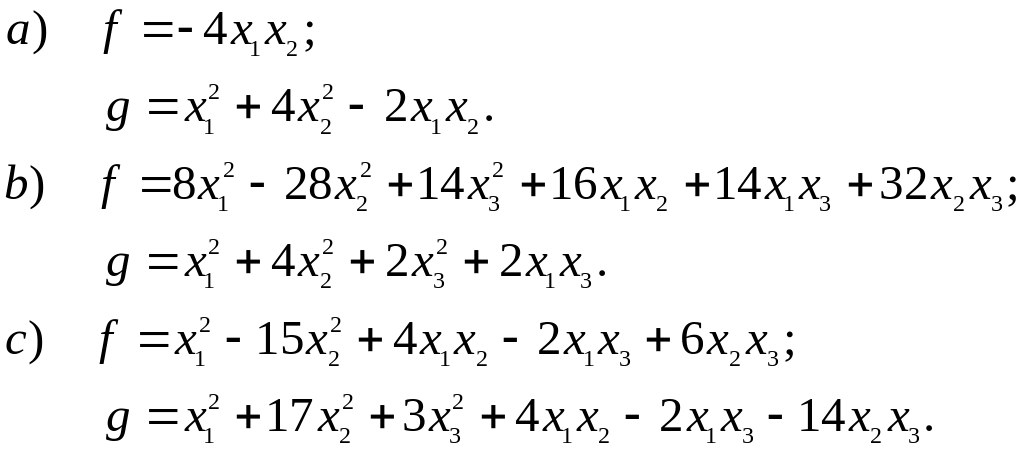
12. Симметрическую эрмитову билинейную форму привести к каноническому виду:
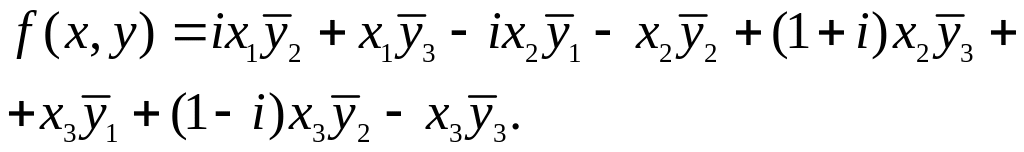
13. Привести к каноническому виду эрмитову квадратичную форму: