Конспект лекций

По Физике за второй семестр.

Работу выполнил: Прошин Андрей Вадимович

Группа СС0604.

Московский Технический Университет Связи и Информатики.

2007 год.

Конспект по физике

за второй семестр.

Часть 3.

Колебания и волны.

Глава 1

Колебания.

Параграф 1.1.

Свободные гармонические колебания.

Уравнение и начальные условия.

Число независимых переменных, необходимых для описания механической системы называется числом степеней свободы.

Рассмотрим систему с одной степенью свободы, для описания которой будем использовать одну переменную X (координата, угол, и т.д.)

В целом ряде задач эта переменная удовлетворяет уравнению вида:

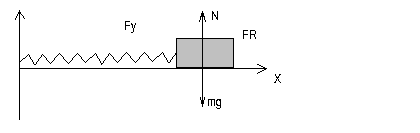
В качестве примера такой системы рассмотрим пружинный маятник без трения.

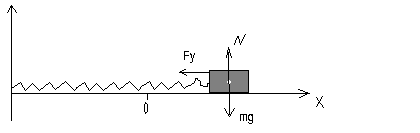
(k – коэффициент жесткости пружины)

- изменение ее длины.

т. О – пружина не растянута.

- называется линейным дифференциальным однородным уравнением 2ого порядка.

Будем искать решение в виде:

Подставим эту функцию в уравнение

Полученное решение называется гармоническими колебаниями.

Система, которая описывается этим уравнением называется гармоническим осциллятором.

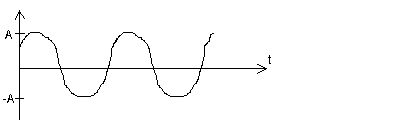
А – амплитуда колебания.

- циклическая частота.

- фаза колебания.

- начальная фаза колебания.

Время Т, в течение которого фаза колебания меняется на

называется периодом колебания.

Частотой колебания называется величина равная

Если х = 0, то , поэтому значение х = 0 называется положением равновесия, а величину х называют смещением.

Полученное решение содержит 2 произвольные постоянные величины: А и

Уравнения гармонических колебаний определяют лишь частоту колебаний.

Рассмотрим на примере пружинного маятника

Для определения амплитуды и начальной фазы необходимы дополнительные условия.

В качестве таких условий обычно используют начальные условия.

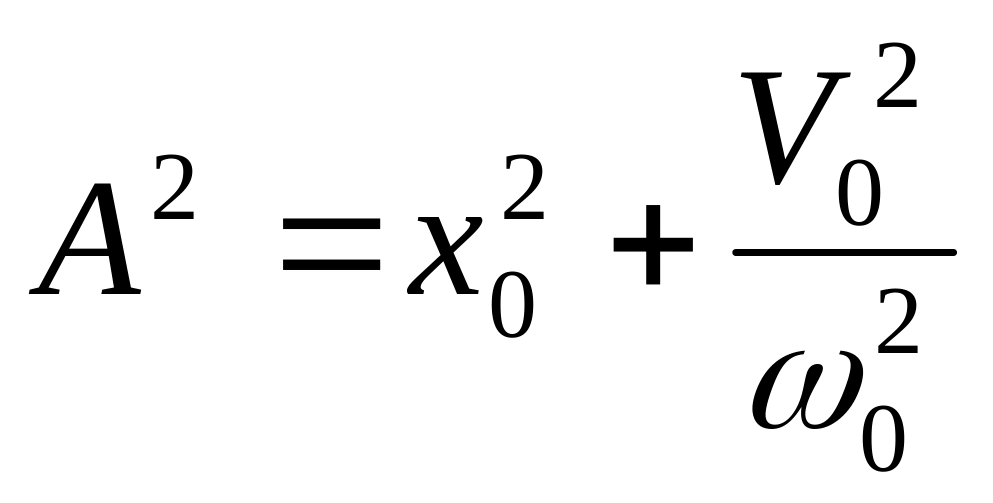
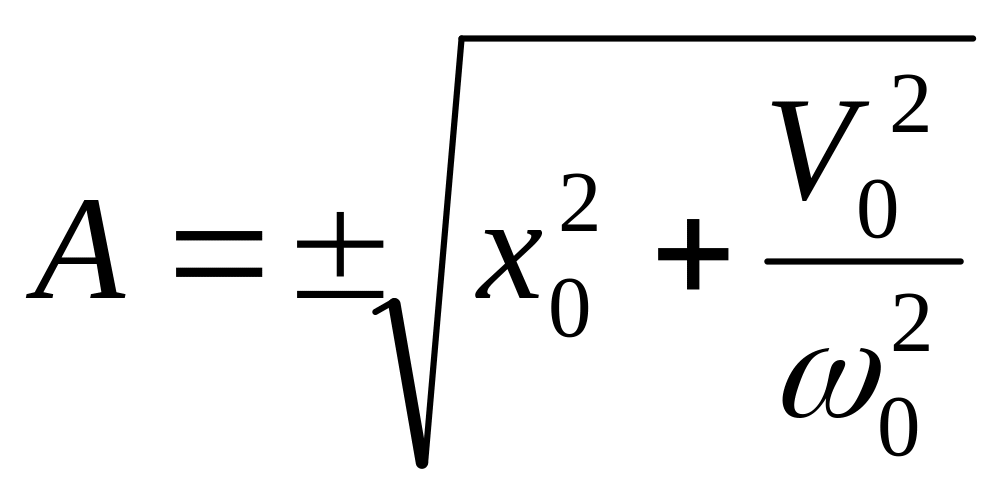
Гармонические колебания.

Параграф 1.2 затухающие колебания.

Рассмотрим систему, в которой есть сила трения, пропорциональная скорости.

коэффициент трения.

Мы получили уравнение вида:

* * *

* * *

Уравнение затухающих колебаний:

для того, что бы решить это уравнение, рассмотрим

Очевидно, что реальная часть комплексного уравнения является уравнением затухающих колебаний, поэтому реальная часть решения комплексного уравнения будет решением уравнения затухающих колебаний.

Будем искать решение в виде:

- фаза колебаний.

Время, в течение которого фаза колебаний меняется на 2 -

называется периодом затухающих колебаний.

Время, в течение которого амплитуда колебания уменьшается в - раз, называется время релаксации.

Заметим, что полученное решение будет справедливо если:

действительная величина, если только .

В этом случае говорят, где система находится в “периодическом решении”.

Если то:

В этом случае никаких колебаний в системе не происходит.

В этом случае говорят, что в системе наблюдается апериодический режим.

- То режим называется критическим. Коэффициент называется либо коэффициентом затухания, либо декрементом затухания. Логарифмический декремент характеризуется затуханием за период, а декремент за единицу времени.