4. Геометрична інтерпретація області припустимих рішень озлп.

Функція

L = с_jх_j (1)

називається цільовою функцією (або лінійною формою) задачі лінійного програмування (ЗЛП), а умови

а_ijх_j  b_i; (i=1,m; j=1,n), x_j  0 (2)

-- обмеженнями задачі ЛП.

Загальною задачею ЛП називається задача, що перебуває у визначенні мінімальної або максимальної величини функції (1) при виконанні умов (2).

Таким чином, треба знайти такі х₁ і х₂, які задовольняють нерівностям і перетворюють у максимум цільову функцію L.

Будемо зображувати пару значень змінних точкою з координатами x₁, x₂ (рис. 1). Оскільки змінні х₁, х₂ повинні бути більше нуля, припустимі їхні значення лежать тільки вище осі Ох₁, (на якій х₂ = 0) і правіше осі Ох₂ (на якій х₁ =0). Це відзначимо штрихуванням, що позначає «припустиму» сторону кожної осі.

Тепер побудуємо на площині х₁0х₂ область припустимих рішень або переконаємося, що її не існує. Рішенням кожної нерівності є на півплощина, що обмежує область припустимих рішень задачі. Покладемо в першому рівнянні х₁ = 0, отримаємо рівняння прямої лінії, перша точка якої

Отримана область є областю припустимих рішень, тобто будь-яка точка області задовольняє нерівностям-умовам, і називається припустимим планом. Зазначимо, що цих рішень - нескінченна множина, тому що будь-яка пара значень вільних перемінних, узята з ОДР, «підходить».

Очевидно, що цільова функція L обертається в максимум в одній з вершин отриманого многокутника. Для визначення цієї вершини геометричним методом побудуємо градієнт цільової функції вектор grad

Частные случаи решения:

1) альтернативное решение – такое решение, при котором цф достигает макс или мин значения не в одной точке, а на целом множестве точек. Решение получаем в виде отрезка, ограниченного двумя вершинами многогранника и ответ записываем в виде:

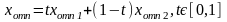
2) неограниченное решение – возможно при неограниченной ОДР ( )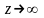

Замечание: при неограниченной ОДР цф не всегда неограниченна, может существовать конечный максимум.

Теорема: Если ЗЛП имеет опт. решение, то цф достигает своего экстремального значения в одной из вершин ОДР.

5.Геометрична інтепретація ОЗЛП для випадку n=2. Графическая интерпретация возможна для ЗЛП, модель которой содержит 2, максимум 3 переменные. Для задач большей размерности геом. интерп. дается обобщением полученных свойств. Рассмотрим частный случай, когда n=2. Ограничения задачи тогда в общем виде записывается такой с-мой:

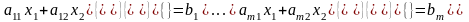
Рассмотрим отдельно ограничение равенства: .

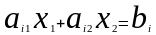Равенство с 2 переменными представляет собой прямую, её можно построить по 2 точкам.

Ограничение-неравенство: 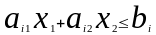– полуплоскость, которая отображается соотв. прямой и может быть определена, например методом контрольной точки. Если с-ма ограничений совместна, то пересечение полуплоскостей образует некоторую общую область, которая называется ОДР задачи, каждая точка этой области может быть решением задачи.

ОДР может быть многоугольником, отрезком, точкой, а так же неограниченной многоугольной областью.

Имеет место такое свойство ОДР: если любые 2 точки ОДР ЗЛП соединить отрезком, то но будет полностью лежать в данном множестве. Такие множества называются выпуклыми.

Для n=2 линии уровня имеют вид и представляют собой семейство параллельных прямых , каждой из которых соотв. определенное значение цф

Используя графич. интерпретацию задачи, процесс поиска опт. решения может быть осуществлен такими этапами: 1) по ограничениям задачи строится ОДР; 2) строятся линии уровня цф, которые задаются так: 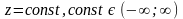; 3) определяется направление возрастания (убывания) цф; 4) Передвигая линии уровня в направлении возрастания, определяют точку минимума как первую точку касания линии уровня и ОДР и точку максимума как последнюю.