16. (13) Транспортні задачі, які мають ускладнення в їх постановці.

В постановке транспортных задач кроме стандартных ограничений на запасы и потребности могут быть учтены и другие дополнительные условия.

1. Если из некоторого пункта отправления перевозки не могут быть перевезены в некоторый пункт назначения. Для решения используется метод блокировки перевозок: тариф по заданному маршруту заменяют большим значением М. Это гарантирует, что перевозка в этой клетке будет равна 0.

2. По заданному маршруту нужно перевести строго определенное количество груза.

В транспортной таблице вносят поправки: 1) в нужную клетку ставится фиксированная 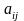, при этом делаются поправки в столбце и и строке, 2) Заданная клетка блокируется большим тарифом М.

3. По заданному маршруту надо перевести не меньше заданного количества груза.

В транспортной таблице вносятся поправки: уменьшают запасы и потребности соответствующих пунктов на и решают полученную задачу. Потом определяют решение исходной задачи, добавив в соответствующую клетку.

4. По заданному маршруту может быть перевезено не больше заданного числа груза:

Транспортная таблица корректируется так: Столбец потребителя заменяем двумя, затем в 1 столбец ставим потребность , а во второй 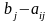и тариф заменяем на М.

17) Постановка Задач нелінійного програмування.

Большинство моделей экономических задач описываются с помощью нелинейных зависимостей. Такие задачи имеют ряд особенностей, которые нужно учитывать при построении методов решений. В частности: 1) ОДР нелинейной задачи может быть произвольным(не обязательно выпуклым многоугольником); 2) Оптимальная точка задачи нелинейного программирования может находиться в любой точке ОДР.

Алгоритм графического способа: 1) По ограничениям строим ОДР; 2) Строим линии уровня ЦФ z=const и определяем направление возрастания; 3) Определяем координаты оптимальных точек 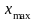и 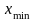и вычисляем значения ЦФ в них.

Если в задаче содержится более чем 2 переменных и она не сводится к двумерной, то существуют аналитические и численные методы поиска ее экстремума. Самым распространенным аналитическим способом решения является метод Лагранжа.

Его идея заключается к сведению решения условной задачи (с ограничением) к безусловной.

18. Геометрична інтерпретація задач нелінійного програмування. У нелінійному програмуванні виокремлюють такі класи: опукле програмування. Для задач опуклого програму-вання існує низка добре обґрунтованих та ефективних методів їх розв'язування. Зазначимо, що задачі лінійного програмування є частковим випадком задач опуклого програмування.

Наголосимо, що коли область допустимих планів є опуклою множиною, а цільова функція є опуклою функцією, то задача математичного програмування має глобальний, єдиний екстремум (якщо такий існує).

Множина S в n-мірному евклідовому просторі називається опуклою множиною, якщо для будь-яких точок (елементів) цієї множини точки належать множині S за всіх значень , які належать відрізку .

Геометричне це означає, якщо та належать до множини 5, то відрізок прямої, що з'єднує ці дві точки, також цілком належить до множини S.

Функція f{X), визначена на опуклій множині лінійного простору (на опуклій множині S), називається опуклою, якщо виконується нерівність

для всіх ц, які належать відрізку .

19. Метод множників Лагранжа. Если в задаче содержится более чем 2 переменных и она не сводится к двумерной, то существуют аналитические и численные методы поиска ее экстремума. Самым распространенным аналитическим способом решения является метод Лагранжа.

Его идея заключается к сведению решения условной задачи (с ограничением) к безусловной.

Рассмотрим пример: (ф-ия Бернулли)

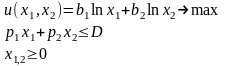
Замечание 1: Метод Лагранжа применим только для задач, в которых ограничения – равенства.

График 1.

Т.к. из теории потребления известно, что оптимальная точка лежит на бюджетной линии, то ограничения в данной модели можно записать в виде равенства.

Решаем методом Лагранжа:

1. Строим функцию Лагранжа

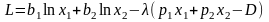
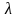- множитель Лагранжа

2. Выписываем необходимые условия extr для функции Лагранжа L

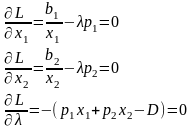
3. Решаем полученную систему уравнений

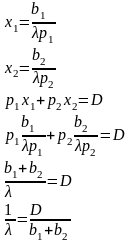
Подставляем найденный множитель

в выражение для Х

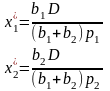
Точка с найденными координатами является точкой extr. Для установления ее характеристик используется матрица 2 производных и исследуется ее характер.