11. Основні теореми двоїстості задач та їх економічний зміст.

Між прямою та двоїстою задачами лінійного програмування іс­нує тісний взаємозв'язок, який випливає з наведених далі теорем.

! Перша теорема двоїстості. Якщо одна з пари двоїстих за­дач має оптимальний план, то інша задача також має розв'язок, причому значення цільових функцій для оптимальних планів до­рівнюють одне одному, тобто 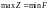, і навпаки.

Якщо ж цільова функція однієї з пари двоїстих задач не обмежена, то друга задача взагалі не має розв'язків.

Якщо пряма задача лінійного програмування має оптимальний план X*, визначений симплекс-методом, то оптимальний план двоїстої задачі Y^* визначається зі співвідношення

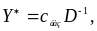
де 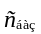— вектор-рядок, що складається з коефіцієнтів цільової функції прямої задачі при змінних, які є базисними в оптимальному плані; D^-1 — матриця, обернена до матриці D, складеної з базисних векторів оптимального плану, компоненти яких узято з початкового опорного плану задачі. Обернена матриця D^-1 завжди міститься в останній симплекс-таблиці в тих стовпчиках, де в першій таблиці містилася одинична матриця.

За допомогою зазначеного співвідношення під час визначення оптимального плану однієї з пари двоїстих задач лінійного програмування знаходять розв'язок іншої задачі.

! Друга теорема двоїстості. Якщо в результаті підстановки оптимального плану прямої задачі в систему обмежень цієї задачі i-те обмеження виконується як строга нерівність, то відповідний i-й компонент оптимального плану двоїстої задачі дорівнює нулю.

Якщо i-й компонент оптимального плану двоїстої задачі додатний, то відповідне i-те обмеження прямої задачі виконується для оптимального плану як рівняння.

! Третя теорема двоїстості. Двоїста оцінка характеризує приріст цільової функції, який зумовлений малими змінами вільного члена відповідного обмеження.

Економічний зміст третьої теореми двоїстості полягає в тому, що відповідна додатна оцінка показує зростання значення цільової функції прямої задачі, якщо запас відповідного дефіцитного ресурсу збільшується на одну одиницю.

12. Визначення оптимального рішення двоїстої задачі по оптимальному рішенню вихідної. Зв'язок між оптимальними рішеннями прямої і двоїстої задач встановлюють наступні теореми.

Т2. План Х₀ = (х₁, х₂, …, х_n) прямої задачі й план U₀ = (u₁, u₂, …, u_m) двоїстої задачі є оптимальними планами цих задач тоді й тільки тоді, коли для будь-якого j = 1,n виконується рівність

,

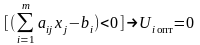тобто якщо в оптимальному розв'язанні прямої задачі якийсь ресурс використовується не повністю, то його "тіньова ціна" дорівнює 0.

Між оптимальними розв'язаннями прямої і двоїстої задач і елементами індексних рядків симплекс-таблиць (індексний рядок – у якій записуються значення L_j), що відповідають цим розв'язанням, існує наступний взаємозв'язок:

,

,

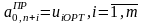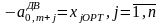де n – кількість змінних прямої задачі;

m – кількість обмежень прямої задачі;

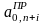- (n+i)-й елемент прямої задачі;

- (m+j)-й елемент двоїстої задачі.

13) Транспортна модель.

Постановка транспортной задачи. Пусть некоторый однородный продукт требуется перевезти от известных поставщиков к заданным потребителям. Общее число поставщиков m: A1, A2…Am. Запас продукции у каждого поставщика a1,a2…am известен. Общее число потребителей n: B1, B2…Bn. Известны заявки на продукцию каждого пункта потребления b1,b2…bn. Также известны стоимости перевозки единицы груза от каждого i-поставщика к каждому j-потребителю, они задаются матрицей тарифов цен. , , 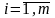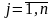. Требуется найти такой план перевозки груза, при котором учитываются все запасы, удовлетворяются все потребности в грузе и минимизируются суммарные транспортные расходы.

Условия транспортной задачи можно представить в виде транспортной таблицы (Табл.)

Построим математическую модель задачи: 1. Переменные: 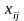- количество груза, перевозимого от i поставщика к j потребителю – общее число переменных равно (m x n);

2. Целевая функция: минимизация суммарных транспортных расходов

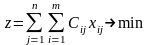; 3. Ограничения : а) на запас:

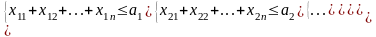
б) на потребности: Перевозка каждому потребителю должна быть не меньше его заявки.

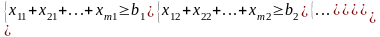
Общее число ограничений n+m

в) Условия неотрицательности:

Данная модель относится к классу задач линейного программирования, но имеет особенности: 1) В ограничениях все коэффициенты при переменных равны 1; 2) Каждая переменная входит только в 2 ограничения.

Эти особенности позволяют построить для решения транспортной задачи более удобный алгоритм, чем симплекс-метод. Модели транспортных задач могут быть открытые и закрытые. Транспортная задача закрытая (сбалансированная) если суммарный запас равен суммарным потребностям.

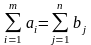
В закрытой задаче все ограничения равенства(общий вид записать). Закрытая транспортная задача – аналог канонической формы ЗЛП, поэтому перед началом решения задачи надо проверить условие сбалансированности, и если надо преобразовать модель к закрытому виду. Это осуществляется введением дополнительных фиктивных пункта отправления (если запас меньше потребностей) либо фиктивного пункта потребления (если запас больше потребностей).

Решение ТЗ осуществляется по общему принципу последовательного улучшения опорных планов. Процесс решения состоит из этапов: 1) Определение начального опорного решения; 2) Оценка этого решения и проверка его оптимальности; 3) В случае необходимости переход к новому лучшему опорному плану путем однократного замещения 1 базисной переменной.

Опорный план ТЗ – матрица перевозок размера mxn в которой число базисных переменных должно быть равно числу линейно-независимых переменных(m+n-1)

Для построения начальных опорных планов можно использовать 1 из методов: 1) метод северо-западного угла; 2) метод минимального элемента; 3) метод двойного предпочтения; 4) метод аппроксимации Фогеля.