ДВОЙНЫЕ, ТРОЙНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

1. Двойной интеграл, его геометрический смысл и основные свойства. Вычисление двойного интеграла сведением к двукратному интегралу.

2.Замена переменных в двойном интеграле. Геометрический смысл якобиана. Двойной интеграл в полярных координатах.

3.Геометрические и механические приложения двойного интеграла.

4.Тройной интеграл и его вычисление сведением к трехкратному. Замена переменных в тройном интеграле (без доказательства). Приложения тройного интеграла. Переход к цилиндрическим и сферическим координатам.

5.Криволинейные интегралы первого и второго рода на плоскости, их свойства, вычисление и некоторые приложения.

6.Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.

7.Поверхностные интегралы первого и второго рода и их вычисление. Основные понятия теории поля. Формулы Стокса, ОстроградскогоГаусса (без доказательства).

По приведенным разделам существует обширная литература с разным уровнем изложения, охватывающая программный материал в различном объеме. Для ориентации ниже предлагается перечень учебников и задачников, которые обычно используются в учебном процессе и не являются библиографической редкостью. Обучающийся может выбрать учебник в соответствии со своим уровнем математической подготовки, степенью образного мышления, индивидуальной формой восприятия языка изложения.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Архипов Т.И. и др. Лекции по математическому анализу: Учебник для университетов и педагогических вузов. - М.: Высшая школа, 1999.

2.Дьяченко М.И., Ульянов П.Л. Мера и интеграл. - М.: 1998.

3.Фихтенгольц Г.М. Курс дифференциального и интегрального исчисле-

ния. Т.1 - 3. - СПб., 1997.

4.Шерстнев А.Н. Конспект лекций по математическому анализу. Казань, 1998.

5.Виноградов И.М. Элементы высшей математики: Учебник для вузов.- М.: Высшая школа, 1999.

6.Гусак Ф.Ф. Высшая математика: Учебное пособие. Т. 1, 2. - М.: 1998.

7.Шипачев В.С. Высшая математика: Учебник для вузов. - М.: Высшая школа, 1985, 1998, 2000.

8.Шипачев В.С. Высшая математика: Учебное пособие для втузов. - М.: Высшая школа, 1994, 2000.

9.	Натансон И.П. Краткий курс высшей математики. - СПб., 1999.
10.	Кузнецов Л.А. Сборник заданий по высшей математике (типовые
	расчеты). - М.: Высшая школа, 1994.

11.Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. - М.: Наука, 1980; 1988.

12.Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Крат - ные интегралы. Ряды. ФКП. - М.: Наука, 1981; 1985.

13.Бугров Я.С., Никольский С.М. Высшая математика: Задачник. - М.:

Наука, 1982.

14.	Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая	математика	в
	упражнениях и задачах. Ч. 1, 2. - М.: Высшая школа, 1986; 1999.
15.	Ильин В.А., Позняк Э.Г. Основы математического	анализа. -	М.:
	Наука, 1980. - Ч. 1; 1982. - Ч.2 .

16.Краснов М.Л. Обыкновенные дифференциальные уравнения. - М.: Высшая школа, 1983.

17.Кудрявцев Л.Д. Курс математического анализа. Т. 1, 2. - М.: Высшая школа, 1981.

18.Кудрявцев Л.Д. Курс математического анализа. Т. 1 - 3. - М.: Высшая школа, 1988.

19.Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник задач по математическому анализу: Интегралы. Ряды. - М.: Наука, 1986.

20.Пискунов Н.С. Дифференциальное и интегральное исчисление для втузов. Т. 1 - 3. - М.: Наука, 1985.

21.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. - М.:

Наука, 1982.

22.Сборник задач по математикедля втузов. Т. 1, 2. / Под ред.: А.В. Ефимова и Б.П. Демидовича. - М.: Наука, 1981; 1986.

23.Федорюк М.В. Обыкновенные дифференциальные уравнения. - М.:

Наука, 1985.

24.Эрроусмит Д., Плейс К. Обыкновенные дифференциальные уравнения. Качественная теория с приложениями. - М.: Мир, 1986.

25.Берман Г.Н. Сборник задач по курсу математического анализа. - М.:

Наука, 1985.

26.Данко П.Е., Попов А.Г., Высшая математика в упражнениях и задачах.

Ч. 1, 2. - М.: Высшая школа, 1973.

27.Будак Б.М., Фомин С.В. Кратные интегралы и ряды. - М.: Наука, 1967.

Для обеспечения необходимого уровня математической подготовки обучающемуся предлагается обратить внимание на следующие рекомендации:

1. Изучение каждого модуля начинайте с запоминания определений основных понятий, утверждений и теорем.

2. Научитесь формулировать теорему, обратную к данной; различать необходимые и достаточные условия в формулировке любой теоремы; записывать суждения с помощью символов математической логики.

3. Разберите доказательства основных теорем раздела и выучите их. 4. Решите не менее 5 - 10 задач на каждую тему в модуле, чтобы

уметь:

4.1. По разделу “Интегральное исчисление функций одной переменной”: находить первообразные, пользуясь методами интегрального исчисления, вычислять определенные интегралы, средние значения функций, площади плоских фигур, длины дуг, центры тяжести и моменты инерции плоских фигур и кривых.

4.2. По разделу “Дифференциальное исчисление функций нескольких переменных”: дифференцировать функции нескольких переменных, выполнять локальное исследование этих функций, определять

координаты стационарных точек и выяснять характер этих точек, находить уравнения касательных плоскостей и нормали к поверхностям, представлять графически функции двух и трех переменных.

4.3. По разделу “Обыкновенные дифференциальные уравнения и системы”: находить общее и частное решения дифференциальных уравнений первого порядка с разделяющимися переменными, линейных, в полных дифференциалах; сводить к уравнению первого порядка дифференциальные уравнения второго порядка специального вида, находить общее решение линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, представлять системы дифференциальных уравнений в виде дифференциального уравнения n- го порядка.

4.4. По разделу “Двойные, тройные, криволинейные и поверхностные интегралы”: вычислять кратные интегралы по простым областям в декартовых, полярных, цилиндрических и сферических координатах, площади плоских фигур и поверхностей, объемы тел, координаты центра тяжести и моменты инерции. Вычислять криволинейные интегралы первого и второго рода, поверхностные интегралы.

5. После изучения каждого модуля выполните тестовые задания предлагаемые в пособии.

Проверка усвоения материала с помощью пакетов тестовых заданий позволяет обучающему выяснить уровень и структуру как знания, так и незнания и достичь определенного стандарта в подготовке, своевременно устранив выявленные пробелы. Одинаковая полнота и равномерность отображения материала контролируемого раздела в каждом пакете тестовых заданий обеспечивает равносильность вариантов пакетов внутри

каждого модуля и возможность сравнения результатов тестируемых в группе, на потоке, курсе, вузе.

Использование пособия в качестве методического обеспечения текущего контроля знаний студентов вносит элементы творчества, целенаправленности и интенсивности в атмосферу учебного процесса, готовит студентов к предстоящей итоговой аттестации в форме тестирования для оценивания уровня учебных достижений студентов в сравнении с требованиями, заложенными в Государственных образовательных стандартах по математическим дисциплинам.

Работа с пособием окажет эффективную помощь студентам заочной и дистанционной форм обучения.

Авторы приносят глубокую благодарность научному редактору профессору В.С. Аванесову, а также профессорам А.А. Пунтусу и А.Г. Яголе за ценные советы по усовершенствованию структуры учебного

пособия и	выражают признательность студентам Балавневу С.В.,
Зелеву А.А.,	Назырову Т.Э., Фаткуллину В.Ф. за помощь в оформлении
рукописи.

1. ПАКЕТЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ТЕМАТИЧЕСКОМУ МОДУЛЮ “ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ”

1.

1. Если функция F(x)

дифференцируема

на

(a;b) и

′

F (x)= f (x) при

любом

x (a,b),

то F(x) называется _________

для __________.

b

2.

Если

A = const , то

интеграл ∫A dx

равен

числу _____________.

a

3.

Установить соответствие

Интеграл

Первообразная (c = const )

1

+ c

1. ∫

1

A. −

dx

x2

x

Б.

2 x ln2 + c

2. ∫2x dx

В. ln 1 − x2 + c

Г. − arccos x + c

3. ∫

dx

Д.

ln

x

+ c

1

Е.

arctg x + c

− x2

2 x

Ж.

+ c

ln2

З.

− arcsin x + c

Ответ: 1. ______, 2. ______, 3. _______.

4.Формулировка теоремы о замене переменной в неопределенном интеграле такова: ______________________________________.

18

5.

Простейшей

(элементарной)

дробью

является

1.

2x −3

2.

(x2 +1)2

3.

x4

4.

x5

.

(x2 + x +1)2

(x2 + x +1)2

(x2 + x +1)2

(x2 + x +1)2

6. Интеграл

∫sin2m+1 x cosn xdx ,

где

m - целое неотрицательное число,

сводится

к

табличному

с

помощью _________________________.

7. Если

f (x)

непрерывная на

[a, b]

функция

и

′

на

F (x)= f (x)

b

[a;b], то по формуле Ньютона - Лейбница ∫ f (x)dx

равен _________.

a

8.

Площадь

фигуры,

ограниченной

графиком

непрерывной

функции r = r(ϕ)

для

α ≤ ϕ ≤ β

и

двумя

лучами

ϕ = α

и

ϕ = β, где

ϕ и

r - полярные координаты, вычисляется по формуле: ___________.

9.

Если

дуга

кривой

задана

уравнением

y = f (x),

a ≤ x ≤b

и

имеет

плотность

ρ = ρ(x),

то

механический

смысл

b

2

интеграла

∫ρ(x)x

′

dx

есть ____________________________.

1+ (f (x))

a

0 ≤ f (x)≤ g(x).

+∞

10. Пусть

α ≤ x < +∞,

Если

∫g(x)dx

+∞

a

сходится,

то

∫ f (x)dx

___________________________________.

a

11. По теореме о среднем

значении,

для

непрерывной на

отрезке [a,b]

функции

f

существует

точка c (a,b), такая что _______________.

Доказательство. _______________________________.

19

	12.	∫(2 − 3x)7 dx
		e−1
	13.	∫ln (x +1)							dx
		0
		1. 1							2. 2
	14.	∫			2x − 3					dx
					x2 − 3x + 2
	15.	∫					dx
					4x −1 − 2x2
	16.	∫		dx
				1 + sin x
	17.	∫			dx
					4	x
					sin

18. ∫ 4x−2x2 dx

19. Площадь			фигуры,
y = e x ,			y = e−x ,
1. 1			2. 2
+∞		dx
20. ∫	x		x
0		+ 2 −
1. 1			2. 2

равен ____________________.

равен	числу
3. 0	4. 2e+1	5. e.

равен ____________________.

равен ____________________.

равен ____________________.

равен ____________________.

равен ____________________.

ограниченной линиями

	x = 0,	x = 1,					равна
	3. e - 1	4. e +			1	− 2	5. e.
					e
	равен
	3. 3	4.	1				5. +∞.
			2

20

2.

1.

Дифференцируемая

на

(a,b)

функция

F(x)

называется

первообразной для функции f (x)

на интервале

(a,b), если ________.

f (x) - интегрируема

[a,b],

b

a

2.

Если

на

то сумма

∫ f (x)dx + ∫ f (x)dx

равна

числу _________________________.

a

b

3.

Установить соответствие

Интеграл

Первообразная (c = const )

1

А.

− ctg x + c

1. ∫

dx

Б.

1

+ c

x2

x

2.

∫

dx

В. ln(1 + x2 )+ c

Г.

tg x + c

1+ x

2

Д.

− arctg x + c

∫

dx

1

3.

Е.

− x + c

2

x

cos

Ж.

arctg x + c

З.

ln x2 + c

Ответ:

1. _______,

2. _______,

3. _______.

4.

Если

u(x) и

v(x) - непрерывно

дифференцируемые

функции,

то формула

интегрирования

по

частям

для определенного

интеграла имеет

вид: _______________________________________.

c

5.

Рациональная

дробь

(x − a)2 (x2 + q2 )

разлагается

в сумму

элементарных

дробей

вида: _______________________________.

21

6.

Интегралы вида ∫R (cos x, sin x)dx , где R(x, y)

- рациональная функция,

сводятся к интегрированию рациональных дробей с помощью

универсальной

подстановки t

= _________, причем

sin x ,

cos x и dx

соответственно

равны _____________, _____________, ____________.

7.

По теореме о

среднем

значении

для

непрерывной

на

отрезке

[a,b]

функции

f (x)

существует

точка

c (a,b)

b

(x)dx

такая,

что

∫ f

равен __________________________.

a

8.

Если

гладкая

кривая задана

параметрическими

уравнениями

x = x(t), y = y(t), t1 ≤ t ≤ t2 ,

то длина

l ее дуги равна _________.

9.

Если

дуга кривой задана уравнением

y = f (x),

a ≤ x ≤b

и имеет

плотность ρ = ρ(x), то момент инерции I x

той дуги относительно оси OX

вычисляется по

формуле: _________________________________.

10.

Если

функция

f (x)

непрерывна

при

0 ≤ x < +∞ ,

то,

+∞

по определению,

∫ f (x)dx

равен __________________________.

a

11.Формулировка теоремы о замене переменной в неопределенном интеграле такова: _______________. Доказательство. ______________.

12. ∫e1−5xdx

равен _____________________.

22

π

	13.	∫2 (x + 2)sin x dx						равен	числу
		0
		1. 1					2. 2	3. 3	4. -1	5. –2.
	14.	∫	x2 + x +1				dx	равен _____________________.
			x3 +1
	15.	∫		dx				равен _____________________.
			12x − 3x2 −11
	16.	∫	dx					равен _____________________.
			1 + cos x
	17.	∫	sin3 x	dx				равен _____________________.
			cos x
	18.	∫	x24+ 9 dx					равен _____________________.
			x

19. Длина дуги

1. 1

∞

20. ∫ dx

1 x(1 + lnx)

1. 1

	кривой		y = ln sin x ,				π	,	π	равна
						x	3
	1			ln3					2		π.
2.			3.			4. ln3				5.
	2			2
											2

равен

2. ln 2

3. 3

4. e

5. +∞.

3.

23

1. По определению, для функции f (x), заданной на (a,b),

совокупность всех ее первообразных называется _________________ и

обозначается __________________________.

2.∫ f ′(x)dx равен _____________________.

3.Установить соответствие

Интеграл

Первообразная

(c = const)

1. ∫xa dx

А.

a xa−1 + c

Б. − sh x + c

В.

sh x + c

1

Г.

tg x + c

2.

∫

dx

xa +1

2

Д.

+ c

sin

x

a +1

Е.

ctg x + c

3.

∫ch x dx

Ж.

xa+1 + c

З.

− ctg x + c

Ответ: 1. ______,

2. ______, 3. _______.

m

ax + b

4. Интеграл

вида

где a,b,c,d — действительные

∫R x,

dx ,

cx + d

числа, m - натуральное число, ad − bc ≠ 0,

R(x, y) - рациональная

функция,

сводится

к

интегрированию

рациональной функции

заменой _________________, причем

dx

равен __________________.

24

5.

Простейшей

(элементарной)

дробью

является

x

3

4

x −1

3

x

2

+

1

1.

2.

3. (

)

4.

.

(x − 2)2

x2 −1

x −1

x2 −1

6.

Интегралы

∫sin2m x cos2n xdx ,

где

m

и n - натуральные числа,

вычисляются

с

помощью

тригонометрических

формул

вида:

1) __________,

2) ___________,

3) ____________,

понижающих

степень

подинтегрального

выражения.

7.

По

теореме

об

оценке

определенного

интеграла,

если

f (x)

непрерывна

на

[a,b],

m - наименьшее,

M - наибольшее значения

b

f (x)

на

[a,b],

то для

∫ f (x)dx

выполняются неравенства: ______.

a

8.

Площадь

криволинейной

трапеции,

(

ограниченной

графиком

не-

прерывной

функции

y =

f

(

x

)

(

f

x

)

≥

)

,

двумя прямыми x = a

и

0

x = b

и

осью

OX , вычисляется по формуле: __________________.

9.

Если дуга

кривой

задана

уравнением

y = f (x),

a ≤ x ≤b

и

имеет

плотность

ρ = ρ(x),

то

механический

смысл

b

ρ(x)x

2

2

интеграла

∫

′

есть __________________________.

1+ (f (x)) dx

a

+∞

+∞

10.

Если

сходится

∫

f (x)

dx ,

то

∫ f (x)dx _______________.

a

a

11.Формулировка теоремы об интегрировании по частям для неопределенного интеграла такова: _________________________.

Доказательство. ____________________________.

25

x

12.

∫sin 1

−

dx

равен __________________.

2

1

13.

∫25(x −1)e5xdx

равен

числу

0

1. 6 +e5

2. 6 − e5

3. 4 + e5

4. 4 − e5

5. e5 .

14.

∫

x − 2

dx

равен __________________.

x2 − x

15.

∫

(2x + 2)dx

равен __________________.

x2 + 2x −1

16.

∫

dx

равен __________________.

1+ cos x

+ sin x

17.

∫ctg2 xdx

равен __________________.

18.

∫

xdx

равен __________________.

( x + 3 x)x

19. Площадь

фигуры,

ограниченной

линиями

y = cosx ,

y = sin x ,

x = 0,

x =

р

,

равна

4

1. 1

2. 2

3. 2

4. 2 − 2

5. 2 −1.

4

x dx

20.

∫

равен

2

(x2 − 4)3

1. 1

2.

1

3. 3

4. 6 3

5. +∞.

6

3

26

4.

1. Неопределенным интегралом от функции f (x) , непрерывной на (a, b), называется _______________________.

2.

По свойству

определенных

интегралов,

если функция

f (x)

интегрируема на [a, b], A =const,

то

b∫

Af (x )dx

равен ___________.

a

3.

Установить соответствие

Интеграл

Первообразная (c = const )

1.

∫

dx

A.

arctg x + c

x

Б.

x +c

В.

10x + c

2.

∫10 x dx

Г.

2 x + c

Д.

arccos x + c

Е.

arcsin x + c

x

3.

∫

dx

Ж.

10

+ c

ln10

1 − x2

З.

10x

+ c

lge

Ответ 1.______ ,

2.______ ,

3. ______.

4.

Согласно

методу

подведения

под

знак дифференциала

для

дифференцируемой функции

u = ϕ(x)

и

интегрируемой функции

g(u)

интеграл

′

равен ______________________.

∫g(ϕ(x))ϕ (x)dx

27

	5. Рациональная	дробь	c	разлагается в сумму
			(x − b)(x − a)2

элементарных дробей вида: ______________________________.

6. Для вычисления интеграла ∫tg m x dx , ( m = 2, 3, 4...)

используется тригонометрическая формула: ______________________.

	7. По	теореме о среднем		значении	для	непрерывной на		отрезке
	[a,b]	функции	f (x) существует			точка	c [a; b]	такая,
			1	b
	что выражение			∫ f (x) dx	равно _______________________.
			b − a
				a

8. Если	гладкая	кривая задана уравнением	y = f (x) , a ≤ x ≤ b , то
длина	ее дуги	l вычисляется по формуле: __________________.

9. Если	дуга	кривой		задана	уравнением	y = f (x) ,	a ≤ x ≤ b и
имеет	плотность		ρ = ρ(x) , то		статический	момент	M y этой дуги
относительно оси			OY	вычисляется по формуле: __________________.

10. Если	функция	f (x)	непрерывна	при	− ∞ < x ≤ b , то,
		b
по определению,		∫ f (x)dx	равен ___________________________.

−∞

11. Теорема о формуле Ньютона - Лейбница имеет вид: ______________.

Доказательство. _________________________________.

28

12. ∫cos (2 − 7x)dx

π

13. ∫2 (1 + 2x) cos x dx

0

1. π

2. 1 + π

14. ∫x31+ x dx

15. ∫	x	2	dx
			+ 2x + 2

.

16.∫cosdx4 x

17.∫sin3 x dx

18. ∫			dx
	x +1(	3	x +1	− x +1)

19. Длина арки		циклоиды
1. 1		2. 2 π
5	dx
20. ∫
0,5	2x −1
1. 1		2. 2

равен ________________.

	равен	числу
	3. 3 + π		4. π - 1	5. π - 3.
	равен _________________.
	равен _________________.
	равен _________________.
	равен _________________.
	равен _________________.
	x = t − sin t;		t [0; 2π]	равна
	y =1 − cos t,
	3. 3 π		4. 4	5.8.

равен

3. 3

4. 4

5. + ∞.

29

5.

1. Для функции f (x), непрерывной на (a, b), символ ∫ f (x)dx

обозначает___________ и, по определению, это есть ______________.

2.∫( f (x) + g(x))dx равен ___________________________.

3.Установить соответствие

	Интеграл					Первообразная (c = const )
	1. ∫ 2 x dx					А.	cos x + c
						Б.	arcctg x + c
							x2
	2. ∫sin x dx					В.		+ c
							2
						Г.	− cos x + c
						Д.	x2 + c
	3.		dx			Е.	arccos x + c
						Ж. − arcctg x + c
		∫1 + x2
						З.	sin x + c
Ответ: 1._______ ,					2._______ , 3. ________.

4.Формулировка теоремы о замене переменной в определенном интеграле имеет вид: ________________________________________.

5. Простейшей

(элементарной) дробью

является

x4

1.

x2

+ x +1

2.

2x + 5

3.

x3 +1

4.

+1

.

x +5

x2 +1

x 2 + 2

x2

−1

30

6. Интеграл вида	∫R (x, a 2 − x2 ) dx , где	R(x, y) -	рациональная
функция, a - действительное положительное число,			приводится к
интегралу	∫R (sin t,cos t) dt	тригонометрической
подстановкой: __________________________.

7. Если f (x) непрерывная на [a,b]	′	[a,b],
	функция и F (x) = f (x) на
	b
то по формуле Ньютона-Лейбница	∫ f (x) dx равен ________________.

a

8. Если фигура ограничена кривой, заданной параметрическими уравнениями x = x(t), y = y(t) ; прямыми x = a, x = b и осью

OX, то ее площадь вычисляется по формуле: ____________________.

9.

Если

дуга

кривой

задана уравнением

y = f (x),

a ≤ x ≤ b

и имеет

плотность

ρ = ρ(x) ,

то

механический

смысл

интеграла

b

2

2

∫ρ(x) f

(x)

1 + ( f

′

dx

есть _____________________________.

(x))

a

+∞

10.

Пусть

a ≤ x < +∞ ,

0 ≤ f (x) ≤ g(x) . Если

∫ f (x) dx

расходится, то

+∞

a

∫g(x) dx __________________________.

a

11.

По теореме

об

оценке

определенного интеграла,

если

f (x)

непрерывна

на

[a,b],

m - наименьшее,

M -

наибольшее

значения

f (x)

на

[a,b],

то ____________. Доказательство. _______________.

31

12.

∫

1

dx

равен ________________.

cos

2

(1−

2x)

0,5

13.

∫8 arctg 2x dx

равен

числу

0

1. π − ln4

2. π − ln16

3. π + ln16

4. π + ln4

5. π.

14.

∫

2x2 + 2x +1

dx

равен _______________.

x

3

+ x

2

15.

∫

2(x −1)

dx

равен _______________.

2

x − 2x − 7

16.

∫

cos3 x dx

равен _______________.

sin x

17.

∫ctg3 x dx

равен _______________.

18.

∫

(

3

dx

x)

x

равен _______________.

x −

19.

Площадь

фигуры,

ограниченной линией

ρ = sin2ϕ,

π

,

ϕ 0,

2

равна

1. 1

2. 2

3.

π

4.

π

5.

π.

2

4

8

e

dx

20.

∫

x

равен

1

lnx

1

1. 1

2. 2

3. + ∞

4. e

5.

.

e

32

6.

1. Если функция f (x) дифференцируема на (a,b) и dF(x) = f (x)dx при любом x (a,b) , то F(x) называется ___________________________.

2. По свойству определенных интегралов, если f (x) и g(x) интегрируемы

b b

на [a,b], то разность ∫ f (x) dx − ∫g(x) dx равна ________________.

aa

3.Установить соответствие

Интеграл

Первообразная (c = const)

1. ∫	x dx		А. − sin x + c
			Б.	1			+ c
2. ∫	dx			2			x
		2	В.	sin x + c
	1− x		Г.	−arcctg x +c
3. ∫cos x dx			Д.		2	x 23 + c
					3
			Е.	− arccos x + c
			Ж.	3			+ c
					x 2
			З.		arccos x + c

Ответ: 1.______ , 2._______ , 3._______.

4.Если u(x) и υ(x) непрерывно дифференцируемые функции, то формула интегрирования по частям для неопределенного интеграла имеет вид:

________________________________.

33

5.

Рациональная дробь

c

разлагается в сумму элементарных

(x − b)(x − a)2

дробей вида ______________________________.

6.

Интегралы вида ∫cos2m+1x sin n x dx ,

где

m - целое неотрицательное

число, сводятся к табличному с помощью _________________________.

7.

Если функция

f (x)

непрерывна и положительна на отрезке

[a,b],

b

то

для

числа

c = ∫ f (x) dx

справедливо

a

1. c < 0

2. c ≤ 0

3. c > 0

4. c ≥ 0

5. c = 0 .

8.

Если

гладкая кривая задана

уравнением

в полярных

координатах

r = r(ϕ) ,

α ≤ ϕ ≤ β,

то

длина

l

ее

дуги

вычисляется

по формуле:____________________________.

9.

Если дуга кривой задана уравнением

y = f (x) ,

a ≤ x ≤ b

и

имеет

плотность ρ = ρ(x) ,

то координаты центра масс

x

и y

вычисляются по

формулам: _____________________________.

10.

Если функция

f (x)

непрерывна при

a ≤ x ≤ b

и

lim

f (x) = ∞, то,

b

x→b−0

(x)dx

по определению,

∫ f

равен __________________________.

a

11. По теореме о дифференцировании интеграла с переменным верхним пределом, если функция f (x) непрерывна на отрезке [a,b], то

			x
производная			F ′(x) = (∫ f (t) dt)′ равна ________________________.
			a
Доказательство. _____________________________.
12. ∫	1	dx	равен ___________________.
	(2 − 5x)

34

	1
13.	∫4x arctg x dx											равен		числу
	0
	1. -2								2. 2			3. π + 2					4. π - 2
14. ∫					x − 7					dx		равен ___________________.
		x		2
					+ 5x + 4
15. ∫				(x − 2)dx					2			равен ___________________.
				8 + 4x − x
16.	∫cos3x dx											равен ____________________.
17.	∫cos 2x cos 4x dx											равен ___________________.
18. ∫		(				dx	4	x				равен ___________________.
					x + x)
															3	t ;			π
19.	Длина						дуги					астроиды	x = cos				t
															3			0,
																t,			2
													y = sin
	1. 1								2. 2			3.	3				4.	π
													2					2
	+∞					xdx
20.	∫											равен
				(x		2		2
	0					+ 2)
	1.		1						2.		1	3. + ∞					4.	π
		4									2							2

35

5. π.

равна

5. π.

5. 0.

7.

1.

Если F(x)

есть

первообразная для

функции

f (x)

на (a, b),

то

совокупность

F(x) + C

называется ________________________

и

обозначается ____________________________.

2.

Если A - число

(A ≠ 0) ,

то

∫Af (x) dx

равен __________________.

3.

Установить соответствие

Интеграл

Первообразная (c = const)

1

А.

1

+ c

1. ∫

dx

x

x

Б. − tg x + c

dx

В.

ctg x + c

2.

∫

Г.

с

2

sin

x

Д.

ln | x | +c

Е.

e x

3. ∫e xdx

+ c

lg e

Ж.

e x + c

З.

− ctg x + c

Ответ: 1. ______ ,

2. _______ ,

3. _______.

4.

Интегралы

вида

∫

dx

и

∫

dx

,

где

a,b,c -

2

ax

+ bx + c

ax2 + bx + c

действительные

числа (a ≠ 0)

приводятся к табличным интегралам с

помощью ____________________________.

5.

Простейшей

( элементарной )

дробью

является

1.

x2 +1

2.

1

3.

x + 2

4.

(x +1)2

.

(x +1)3

x

+1

x +1

x3

+1

36

6. Интеграл ∫R(x, a 2 + x2 )dx , где R(x, y) - рациональная	функция,
a - действительное положительное число, приводится	к интегралу

∫R (sin t,cos t) dt тригонометрической подстановкой вида: _________.

7.Если F(x) - первообразная для непрерывной на [a,b] функции f (x) то

формула Ньютона - Лейбница имеет вид: _______________________.

8. Площадь	фигуры,		ограниченной графиками непрерывных	функций
y = f1(x)	и	y = f2 (x) , f1(x) ≤ f2 (x) и двумя прямыми		x = a, x = b ,
определяется		по	формуле: ____________________________.

9. Если дуга кривой задана					уравнением	y = f (x) , a ≤ x ≤ b			и
имеет		плотность		ρ = ρ(x) , то механический			смысл	интеграла
b			1 + ( f ′(x)) 2 dx
∫ρ(x) f (x)					есть ___________________________.
a
							∞
10. Если		при	a ≤ x < ∞,		0 ≤ f (x) ≤ g(x) и		A = ∫ f (x) dx < +∞,
		∞					a
а	B = ∫g(x) dx ,			то справедливо		соотношение
		a
1. A < B			2. A ≥ B		3. A > B	4. A ≤ B	5. A = B .

11. Если функции f (x) и | f (x) | интегрируемы на [a,b], то для интегралов

b		b
∫| f (x) |dx	и	| ∫ f (x) dx |	верно соотношение ____________.
a		a

Доказательство. _________________________.

37

12.	∫		1			dx
		1 + (1 − x)			2
	e
13.	∫4x ln x dx
	0
	1. e2 +1						2. e2 −1
14.	∫	x	+1	dx
		2	+ 2
		x
15.	∫		3x +1				dx
		3x	2
			+ 2x +1

16.∫tg2 x dx

17.∫sin x cos 4x dx

18.∫ (x2dx+ 4)3

равен _______________.

равен числу

3. 3e2 +1

4. 3e2 −1

5. e2 .

равен _______________.

равен _______________.

равен _______________.

равен _______________.

равен _______________.

19.	Площадь фигуры, ограниченной линиями				y =		1		,	y = 0 , равна
					1 + x2
	1. 1		2. 2π	3. 3	4.		3π			5. π.
							4
	+∞
20.	∫	dx	равен
		x ln x
	e										1
	1. 1		2. 2	3. + ∞				4. 10		5.		.
											e

38

			8.
1.	Если F(x)	и Φ(x) - первообразные для f (x) на (a,b), то выражение
	(F(x) − Φ(x))'		равно ___________________________.
2.	Выражение	( ∫ f (x) dx ) ' равно _______________________________.

3.

Установить соответствие

Интеграл

Первообразная

(c = const)

А.

x + c

1. ∫x dx

Б.

x2 + c

В.

ctg x + c

dx

Г.

x2

+ c

2. ∫

2

2

cos

x

Д.

a x + c

Е.

tg x + c

3. ∫a x dx

Ж.

a xln a + c

З.

a

x

+ c

ln a

Ответ: 1. _______ , 2. ________ , 3. ________.

4.

Интеграл вида ∫

mx + n

dx , где

a,b,c,m,n

-

действительные числа,

ax

2

+ bx + c

(a ≠ 0, m ≠ 0)

сводится

к

интегралу

∫

dx

ax

2

+ bx + c

с помощью ________________________________.

39

5.

Интеграл

∫

dx

равен,

если

(x − a)

k

1. k =1,

2. k >1,

то _________________ ,

то _________________.

6.

Для

вычисления

интеграла

∫ctgm x dx ,

где

m - натуральное

число

большее 1, используется тригонометрическая формула: _____________.

7.

Если

функции

f (x)

и ϕ(x)

интегрируемы

на

отрезке

[a,b],

удовлетворяют

на

нем

неравенству

f (x) ≤ ϕ(x)

и

b

b

A = ∫ϕ(x)dx ,

B = ∫ f (x)dx

(a ≤ b),

то

a

a

1. A < B

2. A > B

3. A ≤ B

4. A ≥ B

5. A = B .

8.

Если

криволинейная

трапеция,

ограниченная

графиком

непрерывной функции

y = f (x) ,

a ≤ x ≤ b ,

вращается

вокруг

оси

OX, то объём тела вращения вычисляется по формуле: _____________.

9.

Если дуга кривой задана уравнением

y = f (x) ,

a ≤ x ≤ b

и

имеет

плотность ρ = ρ(x) ,

то момент инерции

I y

относительно оси OY

вычисляется по формуле: ____________________________________.

10.

Если функция f (x) непрерывна при x [a,c)Υ(c,b], c (a,b)

и функ-

b

ция f (x)

не ограничена в любой окрестности точки c,

то ∫ f (x)dx

a

равен ______________________.

11.Формулировка теоремы об интегрировании по частям в определённом интеграле имеет вид: ______________. Доказательство. _____________.

40

12.

∫

2 − 3x dx

равен __________________.

1

13.

∫4xe2x+1dx

равен

числу

0

1. e3 - e

2. e3 + e

3. 3 e3 - e

4. 3 e3 + e

5. e3.

14.

∫

3x − 2

dx

равен __________________.

2

2x

− 4

15.

∫

2x +1

dx

равен _________________.

(x

2

+ x +

1)

2

16.

∫

cos5x dx

равен _________________.

sin x

sin(x +

π) dx

17.

∫

4

равен _________________.

sin x cos x

18.

∫

xdx

равен _________________.

(

3 x2 + 2 x + 3 x )x

19.

Длина одного витка логарифмической спирали ρ = eϕ, ϕ [0,2π] равна

1. 2 π

2. e 2π

3. e 2π +1

4.

2 (e 2π -1)

5. 2(e 2π -2).

+∞

20.

∫

xe−x2 dx

равен

0

1.

1

2. 2

3. + ∞

4.

0,5

5. e.

41

9.

1.

Если F(x) и Φ(x) - первообразные для

f (x)

на (a ,b) , то их разность

есть __________________________.

2.

Выражение

∫dF(x)

равно ________________________________.

3.

Установить соответствие

Интеграл

Первообразная (c = const)

1. ∫dx

А.

c

Б.

ch x + c

2. ∫sh xdx

В.

sh x + c

Г.

x + c

dx

Д.

arctg x + c

3. ∫

Е.

arcctg x + c

1

+ x

2

Ж.

arcsin x + c

З.

ln(1 + x2 ) + c

Ответ: 1. ______ , 2. _______ , 3. ______.

4.

Интеграл ∫

mx + n

dx , где

a,b,c,m,n

- действительные числа

2

ax + bx + c

dx

(a ≠ 0, m ≠ 0) ,

сводится к

интегралу

∫

ax

2

+ bx + c

с помощью ________________________.

5.

Рациональная

дробь

c

,

где

p2 − 4q < 0 ,

(x − a)(x2 + px + q)

разлагается в сумму элементарных дробей вида: ____________________.

42

6.

Интеграл

∫R(x,

x2 − a 2 )dx ,

где

R(x, y)

- рациональная функция,

a - действительное

положительное

число,

приводится к

интегралу

∫R(sin t,cos t) dt

тригонометрической

подстановкой

вида:

__________________________.

7.

Если функция

f (x)

непрерывна

на

отрезке

[a,b], то

функция

x

F' (x) равна _______.

F (x) = ∫ f (u) du дифференцируема на (a,b)

и

a

8.

Площадь фигуры, ограниченной графиками непрерывных на [a,b]

функций

x = f1( y)

и x = f2 (y) ,

f1(y) ≤ f2 (y)

и двумя

прямыми

y = a , y = b определяется по формуле: __________________________.

9.

Если дуга кривой задана уравнением

y = f (x) , a ≤ x ≤ b

и

имеет

плотность

ρ = ρ(x) ,

то

механический

смысл

интеграла

b

1 + ( f ' (x))2 dx

∫ρ (x) f (x)

есть ____________________________.

a

10.

Если функция f(x) непрерывна при

a < x ≤ b

и

limf (x) =∞,

то, по

b

x→a+0

определению,

∫ f (x) dx

равен ________________________.

a

11. Если функция f(x) непрерывна и положительна на отрезке [a,b], то для

b
∫ f (x)dx	выполняется неравенство __________________________.
a

Доказательство. _______________________.

43

12.	∫		101−2x dx
	π	+2
13.	2	∫x sin(x − 2) dx
		0
	1. 1					2. -3
14.	∫			3(	x −1)	dx
				2	+ x − 2
				x

∫x − 2

15.(x2 − 4x + 5)3 dx

16.

∫

sin5x

dx

cos

x

17.

∫tg3 xdx

18.

∫

4 xdx

(x −

2

4

x

3

+ x)

x

19.

Площадь

фигуры,

x = cos t

;

t [0,

π],

= 2sin t,

y

1. 1

2.

3π

4

+∞

dx

20.

∫

x

2

+ 4x + 5

−∞

1. 1

2. 2 π

равен ________________.

равен	числу
3. 3	4. -1

равен ________________.

равен ________________.

равен ________________.

равен ________________.

равен ________________.

ограниченной линиями равна

3. 3 4. π

равен

3. +∞ 4. π

5. 1 + sin2.

y = 0

и

5. 32π .

5. π2 .

44

	10.
1. Определенным интегралом	функции f (x) на отрезке	[a, b]
называется ________________________________.

2.d ∫ f (x)dx равен ________________________.

3.Установить соответствие

Интеграл

Первообразная (с = const)

1. ∫0 dx

А.

0

Б. ch x + с

В.

sh x + с

2. ∫ch x dx

Г.

c

Д.

arctg x + с

Е.

arcsin x + с

dx 2

Ж.

arccos x + с

3. ∫

З.

ln 1 − x2 + с

1− x

Ответ: 1. ______ , 2. ______ , 3. ______.

4.

Согласно

методу

подведения

под

знак

дифференциала

для

дифференцируемой

функции

u = ϕ(x)

и

функции

g(u)

b

′

интеграл

∫g(ϕ(x)) ϕ (x) dx равен _______________________________.

a

5.

Отношение

двух

многочленов

Pm (x)

,

где

Qn (x)

P (x) = b

+ b x + ... + b

m

xm ,

Q

n

(x) = a

0

+ a x + ... + a

n

xn , b

≠ 0 ,

m

0

1

1

m

an ≠ 0, m ≥ 0, n ≥1 при m < n называется ______________________.

45

6.	Для вычисления интеграла вида ∫sin ax cos bx dx ,						где	a ≠ 0 ,	b ≠ 0
	применяется тригонометрическая				формула: ______________________.
7.	Если	f (x)	и	| f (x) |	интегрируемы		на	[a,b]	и
	b			b
	A = ∫| f (x) | dx ,		B = | ∫ f (x)dx |		( a ≤ b ),	то
	a			a
	1. A < B		2. A ≤ B	3. A > B		4. A = B		5. A ≥ B .

8. Если криволинейная трапеция, ограниченная графиком непрерывной функции y = f (x), 0 ≤ a ≤ x ≤ b , вращается вокруг оси OY,

то объём тела вращения вычисляется по формуле: __________________.

9. Если дуга кривой задана				уравнением		y = f (x),		a ≤ x ≤ b и имеет
плотность	ρ = ρ(x) ,		то	статический		момент		M x	этой	дуги
относительно оси OX			вычисляется		по формуле: ________________.
				+∞			b
10. Несобственный		интеграл		∫ f (x) dx =		lim	∫ f (x) dx называется
				a		b→∞	a
сходящимся,	если ______________________.
11. Если функции		f	и	ϕ интегрируемы			на	отрезке	[a,b]	и
удовлетворяют		на нем неравенству			f (x) ≤ ϕ(x),			то для	интегралов
b		b
∫ f (x) dx и		∫ϕ(x) dx		верно соотношение ___________________.
a		a

Доказательство. _____________________________.

46

12.∫(5 −dx3x)5

13.∫x 2x ln2 2 dx

1. ln4

2. ln4 +1

14. ∫x23x2−−x21 dx

15. ∫(x + 3) x2 + 6x +1dx

16. ∫cos x sin 3x dx

17. ∫ cos3 x dx sin 7 x

18. ∫	x	2	dx	2
			9 − x

равен _________________.

равен числу

3. ln4 −1

4. ln4 + 3

5. ln2 .

равен _________________.

равен _________________.

равен _________________.

равен _________________.

равен _________________.

19. Площадь фигуры, ограниченной линией			ρ =			π	;	π
				cos 2ϕ, ϕ −		4		4	,
равна
1. 1	2. 2	3. 1,5		4. 0,5	5. 0,75.

+∞		dx
20. ∫					равен
		2	x
e		x ln
1. 1			2. 2		3. +∞	4. e	5.	1 .
								2

47

2. ПАКЕТЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ТЕМАТИЧЕСКОМУ МОДУЛЮ “ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ”

1.

1.

По определению, функцией

z = f (x, y)

от

двух переменных x и

y

называется _______________________________.

2.

По

определению, последовательность

точек

Pn

на

плоскости

сходится

к

точке

P0

(Pn (xn , yn )→ P0 (x0 , y0 )),

если

x

n

→ x

0

;

x

n

→ x

0

;

x

n

→

x

0

;

1.

2.

3.

yn

→

y0

.

yn → y0 .

yn → y0 .

4. xn → x0 .

5. yn → y0 .

3.

По определению

(на языке ε − δ),

функция

f (x, y, z)

имеет

предел в точке

M 0 (x0 , y0 , z0 ), равный числу A , если _____________.

4.

Приращение

∆x z

по

переменной

x

функции

z = f (x, y)

вычисляется

по

формуле: _____________________.

5.

Если

приращение

функции

u = f (x, y, z)

представимо

в

виде

∆u = f x′∆x + f y′∆y + f z′∆z + o

(∆x)2

+ (∆y)2 + (∆z)2 ,

то

f (x, y, z)

называется ___________________________.

48

6.

Если

z = f (x, y) -

дифференцируемая функция

переменных

x

и y ,

причем

y = ϕ(x)

-

дифференцируемая

функция

независимой

переменной

x , то производная сложной функции

z = f (x,ϕ(x))

вычисляется по формуле: _____________________________________.

7.

По

определению,

полным

дифференциалом

первого

порядка

функции

z = f (x, y)

называется ____________________________.

8.

Если

P0

-

точка

минимума

дифференцируемой

функции

u = f (x, y),

то

для

первого

дифференциала

du

справедливо

1.

du > 0

2.

du < 0

3. du = 0 .

9.

Касательная

плоскость

к

поверхности

S :

z = f (x, y)

( f

-

дифференцируемая

функция)

в

точке

P0 (x0 , y0 ,z0 )

задается

уравнением _______________________________________.

10.

Производная

дифференцируемой

функции

u = f (x, y, z)

в

точке

P0 (x0 , y0 ,z0 )

в

направлении

вектора

(cos α, cos β, cos γ)

вычисляется по формуле: _________________.

n

11.

По

теореме

о

дифференцируемости

сложной

функции,

если

u = f (x, y)

- дифференцируемая функция

переменных

x и y , а

x = ϕ(t),

y = ψ(t)

-

дифференцируемые

функции

независимой

переменной

t ,

то

производная

функции

u = f (ϕ(t),ψ(t))

вычисляется по формуле: _______________.

Вывод. ______________.

49

12. Областью

определения

функции

двух

переменных

z = x2 + y 2 − 9 является ___________________________________.

13.

lim

sinxy

x→0

xy

y→0

1. 1

2. 0

3. ∞

4.

1

5. Не существует.

2

14.

Если

z = cos(x2 y + 2x + y 2 ) ,

то

частная

производная

z′y

равна ________________________.

15.

Если

z = ln(u3 + 3v) ,

где u =

x − y ,

v =

x

,

то частная

z′x

y

производная

равна _______________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + y 2 + z 2 + 6z − 4x + 8 = 0 , то

a) частные производные z′x и z′y

равны ____________, ___________;

б) дифференциал dz имеет

вид: _____________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией поверхности в точке

P0 (2;1;-1) имеет вид: ___________.

17.

Стационарной

точкой

для

функции

z = x2 + y 2 − xy +1

является точка _______________, причем у

функции

в этой точке

1. Максимум.

2.

Минимум.

3.

Нет экстремума.

18.

Если функция

z = e

x 2 − y

2

то смешанная

производная

′′

,

zxy

равна _______________________________.

50

2.

1. Поверхностью уровня функции u = f (x, y, z) трех переменных x, y, z

называется _______________________________.

2.

Множество

точек

P(x, y) R 2

называется открытым

кругом

радиуса

r

с

центром

в

точке

P (x

0

, y

0

),

если

для

d = (x − x

0

)2

+ (y − y

0

)2

0

справедливо

утверждение

1. d ≤ r

2. d ≥ r

3. d = r

4. d < r

5. d > r .

3.

Если

lim

f (x, y)= A ;

lim

g(x, y)= B ,

B ≠ 0,

то

x→x0

x→x0

y→y0

y→y0

f (x, y)

lim ( ) равен ____________________________. x→x0 g x, y

y→y0

4. Частной производной по

y функции z = f (x, y) в точке

P0 (x0 , y0 ) называется __________________________.

	5. Если функция	∂f (x, y)		имеет частную производную по x , то
		∂y

эта производная называется __________ и обозначается ____________.

51

6. Если z = f (x, y) - дифференцируемая функция переменных x и y , а

x = ϕ(t),	y = ψ(t) - дифференцируемые	функции	независимой
переменной	t , то производная сложной	функции	z = f (ϕ(t),ψ(t))
вычисляется по формуле _______________________.

7. По определению, дифференциалом	второго порядка	функции
z = f (x, y) называется _______________________________.

8.	Если	дифференцируемая			функция		u = f (x, y, z)	достигает
	экстремума в		точке	P0 (x0 , y0 ,z0 ),			то ______________________.
9.	Нормаль		к	поверхности			S : F(x, y, z)= 0
	( F -	дифференцируемая функция)				в	точке	P0 (x0 , y0 ,z0 )

задается

уравнением _____________________________.

10.

Функция

z = f (x, y)

имеет

условный

максимум

в точке

P0 (x0 , y0 ),

принадлежащей

кривой

Г:

ϕ(x, y)= 0

(ϕ(x, y)= 0 - уравнение связи),

если __________________________.

11.

При выполнении

условий

теоремы о

неявной

функции

y = y(x),

заданной

уравнением

f (x, y)= 0 , формула

для

вычисления

производной

dy

имеет вид: _____________. Вывод. __________.

dx

12.

Областью

1

определения

функции

двух

переменных

z =

является ________________________.

2

− y 2

16 − x

52

13.

lim

xy

2 −

xy + 4

x→0

y→0

1. 0

2.

∞

3.

-4

4.

4

5. Не существует.

14.

Если

z = arctg (x2 + y3 ) ,

то

частная

производная

z′x

равна _______________________.

15.

Если

z = ln (u3 + v) ,

где

u = 2x −

y ,

v =

x

,

то

частная

y

производная

z′y

равна _____________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + y 2 + z 2 − xy + 3z = 7 ,

то

а) частные

производные

z′x

и

z′y

равны __________, _________;

б) дифференциал

dz

имеет

вид: ___________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией

поверхности

в

точке

P0 (2;1;1)

имеет вид: _____________________________.

17.

Стационарной точкой для функции

z = 2x2 + y 2 − xy + 2

является

точка _________________,

причем у

функции

в

этой

точке

1. Максимум.

2.

Минимум.

3.

Нет экстремума.

18.

Если

функция

z = ctg (x + y

2

),

то

′′

смешанная производная zxy

равна_____________________________________.

53

3.

1. По определению, функцией

u = f (x, y, z)

трех

переменных

x , y , z называется ______________________________.

2. Множество	точек	P(x, y) R2		называется	замкнутым
прямоугольником, если		для	a1 <b1,	a2 <b2	справедливо

1.a1 < x < b1;a2 < y < b2.

3.a1 < x ≤ b1;a2 < y ≤ b2.

2.a1 ≤ x ≤ b1;a2 ≤ y ≤ b2.

4.a1 ≤ x < b1;a2 ≤ y < b2.

3.	По	определению		(на языке ε −		δ ), предел		lim	f (x, y)= ∞,
							x→x0
	если ____________________________.							y→y0
4.	Приращение		∆y z		функции	z = f (x, y)	по	переменной
	y	вычисляется		по	формуле: ________________________________.
5.	Если	приращение			функции	z = f (x, y)	представимо			в
	виде	∆ z = f x′ ∆ x + f y′ ∆ y + o				(∆x)2 + (∆y)2	,	то	f (x, y)

называется _______________________________.

54

6.

Если

z = f (x, y)

-

дифференцируемая функция

переменных x и

y , причем

x = ψ(y)

-

дифференцируемая

функция

независимой

переменной

y ,

то

производная

сложной

функции

z = f (ψ(y), y)

вычисляется

по формуле: ___________________________________.

7.

По

определению,

частным

дифференциалом

d y z

функции

z = f (x, y)

по

y

называется ________________________________.

8.

Если

′

, y0 )

′

и

′′

′′

f x (x0

= f y (x0 , y0 )=0

A = f xx (x0 , y0 )

, B = f yy (x0 , y0 ),

C =

′′

то

точка

P0 (x0 , y0 )

не

является точкой

f xy (x0 , y0 ),

экстремума функции

z = f (x, y)

при условии __________________.

9.

Координаты

вектора

нормали

к

поверхности

S :

z = F(x, y)

( F - дифференцируемая функция)

в

точке

P0 (x0 , y0 ,z0 )

равны ___________________________________.

10.

Градиентом

дифференцируемой

в

точке

P0 (x0 , y0 ,z0 )

функции

u = f (x, y, z)

называется

вектор ___________________.

11.

Уравнение

касательной

плоскости

к

поверхности

S : F(x, y, z)= 0

( F - непрерывно

дифференцируемая

функция) в

нестационарной точке

P0 (x0 , y0 ,z0 )

имеет вид: _______________.

Вывод. ____________________________________.

12. Областью определения функции двух переменных

55

z = x2 + y 2 − 4 является __________________________.

13.

lim

sin xy

y

x→0

y→0

1. 1

2. 0

3. ∞

4. -1

5. Не существует.

14.

Если

z = ln(y 2 + 2xy + 3x) ,

то

частная

производная

z′y

равна ______________________________.

15.

Если

z = tg (u 2 −

v) ,

где

u = 2x + 3y ,

v = xy ,

то

частная производная

z′x

равна _____________________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + y 2 + z 2 + 6y + 4x = 8 ,

то

а) частные

производные

z′x

и

z′y равны _________, _________;

б) дифференциал

dz

имеет

вид: ____________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией

поверхности

в

точке

P0 (−1;1;2)

имеет вид: ____________________________ .

17.

Стационарной

точкой

для

функции

z = xy − 2x2 − y 2 −1

является точка _____________,

причем у

функции в

этой

точке

1. Максимум.

2.

Минимум .

3.

Нет экстремума.

18.

Если

функция

z = cos (3x2 − y −3 ),

то

смешанная

производная

′′

равна ________________________________.

zxy

56

4.

1.Областью изменения функции f (x, y) двух переменных x и y

называется ____________________________.

2.По определению, точка P0 (x0 , y0 ) называется внутренней точкой

множества E , если ________________________________________.

3. Если	функции	f (x)	и	g(x)	имеют	пределы:
lim	f (x)= A,	lim g (x)= B,			то	предел	суммы
x→x0		x→x0
y→y0		y→y0

lim (f (x)+ g(x)) равен _________________________________.

x→x0 y→y0

4. Частной	производной функции z = f (x, y)	по	x	в точке
P0 (x0 , y0 )	называется _____________________________________,

ееобозначение _________________________________.

	5. Для		дважды	дифференцируемой		функции			z = f (x, y)
	вторая		частная	производная	∂2 f		,	по	определению,
					∂y∂x
	есть ___________________________________________,
	она	называется _______________________________.

57

6. Если u = f (x, y, z)	- дифференцируемая функция переменных x , y , z ,
причем y = ϕ(x),	z = ψ(x) - дифференцируемые функции независимой
переменной x , то	производная сложной функции u = f (x, ϕ(x), ψ(x))

вычисляется по формуле: ___________________________.

7.	Если	функция	z = z(x, y)		неявно	задана уравнением F(x, y, z) = 0
	(F - дифференцируемая				функция		переменных		x , y , z ),	то
	частная производная ∂z			вычисляется по формуле: ________________.
			∂y
8.	Если	P0 (x0 , y0 ,z0 )		-	точка	максимума			дифференцируемой
	функции		u = f (x, y, z) ,		то	для	первого	дифференциала		du
	справедливо
	1. du > 0				2. du < 0				3. du = 0.
9.	Нормаль к		поверхности		S :	z = f (x, y)		(f - дифференцируемая
	функция) в точке P0 (x0 , y0 ,z0 ) задается уравнением ______________.
10.	Функция		u=f (x, y, z)		имеет		условный	минимум в		точке
	P0 (x0 , y0 ,z0 ),		принадлежащей			поверхности			S : ϕ(x, y, z)=0
	(ϕ(x, y, z)= 0		уравнение связи), если ___________________________.
11.	Для	дифференцируемости			функции		z = f (x, y)	в	точке, необходимо,

чтобы _____________________. Доказательство. ___________________.

58

12.

Областью

определения

функции

двух

переменных

z =

1 − (x2 + y 2 )

является ___________________________________.

13.

lim

x

y − x

x→0

y→0

1. 1

2. 0

3. ∞

4. -1

5. Не существует.

14.

Если

z = cos (x2 y + 2x + y2 ),

то

частная

производная

z′x

равна ___________________________________.

15.

Если

z = arctg (u 2 + 2v),

где

u =

x

,

v = 2x + y ,

то

y

частная производная

z′y

равна _____________________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + y 2 + z 2 − 6y + 4z + 4 = 0 ,

то

а) частные

производные

z′x

и

z′y

равны __________, ________;

б) дифференциал

dz

имеет

вид: ______________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией

поверхности

в

точке

P0 (2;1;−1)

имеет

вид: _______________________________________.

17.. Стационарной

точкой

для

функции

z = 2xy − x2 − 3y 2 − 2

является точка _____________,

причем

у функции в

этой

точке

1. Максимум.

2. Минимум.

3. Нет экстремума.

18.

Если

функция

z = ln (4x2 − y3 ) ,

то

смешанная

производная

′′

равна ______________________________.

z xy

59

5.

1.

Областью

определения

функции

трех

переменных

x, y, z

называется _____________________________.

2.

Множество

точек

P(x, y) R2

называется

замкнутым

кругом

радиуса

r

с

центром

в точке

P0 (x0 , y0 ), если

для

d =

(x − x0 )2 +(y − y0 )2

справедливо

1. d < r

2. d ≤ r

3. d = r

4. d > r

5. d ≥ r .

3.

По

определению

(на языке приращений),

функция

f (x,y)

непрерывна

в точке

P0 (x0 , y0 ),

если _____________________.

4.

Полное

приращение

∆z

функции

z= f (x, y)

вычисляется

по формуле: _________________________.

5.

Если

функция

∂f (x, y)

имеет

частную

производную

по y, то

∂y

эта производная называется _________ и обозначается _________.

6.

Если

z= f (u,v)

-

дифференцируемая

функция

переменных

u и

v,

причем

u = ϕ(x, y),

v = ψ(x, y) -

дифференцируемые

функции независимых

переменных

x

и

y,

то

частная

производная

∂z

вычисляется

по

формуле: _________________.

∂x

60

7.

Если

z= f (x, y)

дважды

непрерывно

дифференцируемая

в

окрестности

точки

P0 (x0 , y0 )

функция,

то

для

ее

смешанных

производных

верно

соотношение _________________.

8.

По

определению,

функция

w=f (x,y,z)

имеет

минимум

в

точке

P0 (x0 , y0 ,z0 ),

если

существует

такая

окрестность

точки

P0 (x0 , y0 ,z0 ),

что ____________________.

9.

Касательная

к

кривой

Г: f (x, y) = 0

( f

- дифференцируемая

функция)

в точке

P0 (x0 , y0 ) задается

уравнением _____________.

10.

Если

вектор

n

образует

угол

ϕ

с

grad f (P0 ) ,

то

производная по направлению

∂f

(P )

равна ______________.

∂n

0

11.

Уравнение

нормали

к

поверхности

S : F(x,y,z) = 0

( F -

непрерывно

дифференцируемая

функция)

в

неста-

ционарной точке P0 (x0 , y0 ,z0 ) имеет вид: _________________.

Вывод. ____________________________.

12.

Областью

определения

функции

двух

переменных

z = ln(−x − y)

является _______________________________________.

13.

lim

2 −

xy + 4

x→0

xy

y→0

1.

0

2.

0,25

3. -0,25

4.

∞

5. Не существует.

61

14. Если	z = arcsin(2xy + 3 y ) ,	то	частная производная z′y
равна _______________________.

15.

Если

z =

u2 + v ,

где

u = x sin y ,

v = 5y +3x ,

то

частная

производная

z′x

равна ______________________.

16.

Если

функция

z (x, y)

задана

неявно

уравнением

2x2 − y2 + z2 −6x + 2y + 6 = 0, то

а) частные производные

z′x

и

z′y

равны _________, _________;

б) дифференциал dz

имеет вид: ______________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией

поверхности

в

точке

P0 (1;−1;1)

имеет

вид: _________________________________.

17.

Стационарной

точкой

для

функции

z = x2 + y2 − xy +3x +1

является точка _____________,

причем

у

функции в

этой

точке

1. Максимум.

2.

Минимум.

3. Нет экстремума.

18.

Если

функция

z = tg(x2 − y) ,

то

смешанная

производная

′′

равна _________________________________.

z xy

6.

1. Линией уровня функции z = f (x, y) называется ________________.

62

2. По определению, множество

E

ограничено, если

существует

число

c > 0

такое,

что

для

любой

точки

P (x, y) E

выполняется

неравенство

1.

x

< c

2.

y

< c

3. x2 + y 2 < c

5.

x − y

< c .

4.

x + y

< c

3. Если	lim f (x, y) = A	и	c = const ,	то
	x→x0
	y→y0

lim c f (x, y) _____________________________.

x→x0 y→y0

4. Разность

f (x0 + ∆x, y0 ) - f (x0 , y0 ) называется _________________.

5.	Для	дважды дифференцируемой					функции	z= f (x, y)		вторая
	частная производная			∂2 f	,	по определению,		есть _____________,
				∂ x ∂ y
	она называется ______________________________.
6.	Если		w = f (u, v, z)	дифференцируемая функция					переменных
	u, v,	z ,	причем	u = ϕ(x, y),			v = ψ(x, y),		z = g(x, y)
	дифференцируемые функции					независимых		переменных		x и y ,
63

то частная производная ∂∂xw вычисляется по формуле: ____________.

7.

Если

функция

z = z (x, y)

неявно

задана

уравнением

F (x,

y, z) = 0

( F

- дифференцируемая

функция

переменных

x, y , z ),

то

частная

производная

∂ z

вычисляется

∂ y

по

формуле: _______________________________.

8.

Если

′

(x0 , y0 )

′

(x0

, y0 )= 0

и

A

′′

, y0 ),

f x

= f y

= f xx (x0

B =

′′

C =

′′

то

точка

P0 (x0 , y0 )

f yy (x0 , y0 ),

f xy (x0 , y0 ),

есть

точка

минимума

функции

z= f (x, y)

при

выполнении условий______________________________.

9.

Нормаль

к

кривой

Г:

f (x, y) = 0

( f

-

дифференцируемая

функция)

в точке

P0 (x0 , y0 )

задается уравнением ______________.

10.

В

задаче

на

условный

экстремум

для

функции

z = f (x, y)

с

уравнением

связи

ϕ(x, y)= 0

функция

Лагранжа

равна _____________________________.

11.

По

теореме

о

необходимых

условиях

существования

экстремума,

если

функция

z= f (x, y)

имеет

экстремум

в точке

P0 (x0 , y0 ), то ___________. Доказательство. _____________.

12.

Областью

определения

функции

трех

переменных

u =

x2 + y2 + z2 −9

является ________________________________.

64

13.

lim

x − y

(x + y)3

x→0

y→0

1. 1

2. ∞

3. 0,5

4. 0

5. Не существует.

14.

Если

z = ln(y 2 + 2xy + 3x), то частная производная

z′x

равна _______.

u

u = 2x +3y ,

v = xy ,

15.

Если

z = cos

,

где

то

частная

v

производная

z′y

равна ____________________________.

16.

Если

функция

z(x,y)

задана

неявно

уравнением

x2 + y2 − z2 +6xy − z = 8 , то

а) частные

производные

z′x

и

z′y

равны ________, ________;

б) дифференциал d z

имеет вид: _____________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией поверхности в точке

P0

(1;1;0) имеет вид: __________.

17.

Стационарной

точкой

для функции

z = x2 + y 2 − xy + x + y − 3

является

точка ______________, причем

у функции в этой точке

1. Максимум.

2. Минимум.

3. Нет экстремума.

18.

Если

функция

z = arcsin (x3 − y) ,

то

смешанная

производная

′′

равна _______________________________.

zxy

65

7.

1.Функция от двух переменных, заданная неявно, определяется уравнением ______________________________.

2. Множество	точек	P(x, y)	R 2	называется	открытым
прямоугольником, если		для	a1 < b1, a2 < b2		справедливо

1.a1 ≤ x < b1;a2 ≤ y < b2 .

3.a1 < x < b1;a2 < y < b2 .

2.a1 < x ≤ b1;a2 < y ≤ b2 .

4.a1 ≤ x ≤ b1; .a2 ≤ y ≤ b2 .

3. По определению	(на языке окрестностей), функция	u = f (x, y, z)
имеет предел в	точке P0 (x0 , y0 , z0 ) , равный	числу	A,
если ___________________________________.

	4. Выражение	lim	f (x0 , y0 + ∆y) − f (x0 , y0 )
			∆ y
		∆y→0

называется _____________________________.

5. Если функция	∂f (x, y)	имеет частную производную по x , то эта
	∂ x

производная называется ___________ и обозначается _______________.

66

	6. Если	z = f (u,v) - дифференцируемая			функция переменных	u
	и v ,	причем	u = ϕ(x, y) ,	v = ψ(x, y) -	дифференцируемые функции
	независимых		переменных	x и y ,	то частная производная	∂ z
						∂ y

вычисляется по формуле :____________________.

7.	По теореме о смешанных производных,			для функции	z = f (x, y)
	равенство f xy" (x0 , y0 ) = f yx" (x0 , y0 ) верно, если _________________.
8.	По	определению,	экстремумами	функции	u = f (x, y, z)
	называются ________________________________.

9.	Координаты	вектора	нормали	касательной			плоскости	к
	поверхности	S : z = f (x, y) ( f - дифференцируемая функция) в точке
	P0 (x0 , y0 , z0 )	равны ___________________________.
10.	Наибольшее	значение	производной		∂ f	(P )	достигается	в
					∂n	0
	направлении	n , составляющим с grad f (P0 ) угол _______________.

11. По теореме о дифференцируемости сложной функции			u = f (x, y) , если
f - дифференцируемая	функция переменных	x и	y , а x = ϕ(t) ,
y = ψ(t) - дифференцируемые функции независимой переменной t , то
производная функции	u = f (ϕ(t),ψ(t)) вычисляется		по

формуле: ___________________. Вывод. _______________________.

67

12.	Областью		определения		функции		трех	переменных
	u =		1	является ______________________________.
		4 − x2 − y 2 − z 2
13.	lim	sin xy
		x
	x→0
	y→0
	1. 1		2. 0	3. ∞		4. -1	5. Не существует.
14.	Если		z = tg (x3 + y −2 ) ,		то	частная	производная		z′y

равна ________________________________.

15.

Если

z = arcctg (u 2 + 2v),

где

u =

x

,

v =

x +3y ,

то

y

z′x

частная

производная

равна ___________________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + z2 −5yz +3y = 46 ,

то

а) частные производные

z′x

и

z′y

равны ___________, __________;

б) дифференциал

dz

имеет

вид: ___________________________;

в) уравнение касательной плоскости к

заданной этой функцией

поверхности в точке P0 (1,2,−3) имеет вид: ____________________.

17.

Стационарной

точкой

для

функции

z = xy − x2 − y2 + x −5y + 2

является

точка ____________,

причем

у

функции в этой

точке

1. Максимум.

2.

Минимум.

3.

Нет экстремума.

18.

Если

функция

z = ln (3x2 − 2y 2 ),

то

смешанная

′′

равна ___________________________________.

производная zxy

68

8.

1.

Графиком

функции двух переменных

является ________________.

2.

Окрестностью точки

P0(x0,y0) R2

называется _________________.

3.

По

определению

(на языке

ε −δ),

функция

f (x, y)

непрерывна в

точке

P0(x0,y0),

если ________________________.

4.

Разность

f (x0 +∆x, y0 +∆y) − f (x0, y0)

называется _________________.

5.

Для дважды дифференцируемой функции

z = f (x, y)

вторая

частная

производная

∂2 f

,

по определению, есть ______________________.

∂ y

2

6.

Если

w = f (u,v, z)

- дифференцируемая функция переменных

u, v, z,

причем

u = ϕ(x, y) ,

v = ψ(x, y) ,

z = g(x, y)

-

дифференцируемые

функции

независимых

переменных

x

и

y ,

то

частная производная

∂ z

вычисляется

по

формуле: ______________________________.

∂ y

7.

Если функция

y = y(x)

неявно

задана

уравнением

f (x, y) = 0 ( f -

дифференцируемая

функция переменных

x и

y ),

то производная

dy

вычисляется по

формуле: _________________________________.

dx

69

8. По определению, функция u = f (x, y, z)		имеет	максимум в	точке
P0(x0,y0,z0), если	существует такая	окрестность этой		точки,
что ________________________________________.

9.Уравнение f x′ (x0 , y0 ) (x − x0 ) + f y′ (x0 , y0 ) ( y − y0 ) = 0

является___________________________ для кривой Г, заданной уравнением вида: _________________________________.

10. Если функция u = f (x, y, z)	с уравнением	связи ϕ(x, y, z) = 0 имеет
в точке P0 (x0 , y0 , z0 )	условный	максимум,	то функция
Лагранжа удовлетворяет	системе _____________________.

11. По теореме	о	необходимых	условиях	существования
экстремума,	если	функция	z = f (x, y)	имеет экстремум

в точке P0 (x0 , y0 ) , то ___________. Доказательство. _____________.

12. Областью		определения	функции	трех	переменных
u =	1	является _______________________________.

x2 + y 2 + z 2 −16

13. lim	xy
	(x2 + y 2 )2
xy→→00
1. 1	2. ∞		3. 0,5	4. 0	5. Не существует.

70

14. Если	z = ctg (x−3 + y 2 ),	то	частная	производная z′x
равна _______________________________.

15. Если	z =	u 2 + 2v ,	где	u = x sin y ,	v = 5y + 3x ,	то частная
производная		z′y	равна ________________________________.

16. Если	функция		z(x, y)		задана	неявно	уравнением
x2 + y 2 − xy − yz = 0 ,			то
а) частные производные			z′x и	z′y	равны ___________, __________;
б) дифференциал		d z	имеет	вид: ___________________________;
в) уравнение		касательной		плоскости		к заданной		этой
функцией		поверхности		в	точке	P0 (0,2,2)		имеет

вид: _______________________________________.

17. Стационарной		точкой		для	функции
z = 2xy − x2 − 3y 2 + 2x − 6y − 3			является	точка ________________,
причем у	функции в	этой	точке
1. Максимум.	2.	Минимум.		3.	Нет экстремума.

18. Если	функция z = arctg (x + y 2 ), то смешанная	производная
′′	равна __________________________________.
z xy

71

9.

1.	Функция	одной	переменной,		заданная	неявно,	определяется
	уравнением ________________________________.
2.	Множество	называется		открытым,	если _______________________.
3.	Если lim	f (x, y) = A ,		lim g(x, y) = B , то		предел	произведения
	x→x0			x→x0
	y→y0			y→y0

lim ( f (x, y) g(x, y)) ____________________________________.

x→x0 y→y0

	4. Предел	отношения	lim	f (x0 + ∆x, y0 ) − f (x0 , y0 )
				∆x
			∆x→0

называется ___________________________________________________.

5. Если	функция	∂ f (x, y)	имеет частную производную по y , то
		∂ x
эта	производная	называется __________________________________

иобозначается _____________________________________________.

	6. Если	u = f (x, y, z) - дифференцируемая			функция		переменных
	x, y, z,	причем	z = ϕ(x, y)	- дифференцируемая			функция
	независимых переменных		x и y ,	то частная		производная		∂u
								∂ x

вычисляется по формуле: _______________________________________.

72

7. По определению, частным дифференциалом

d x z по

x

функции z = f (x, y) называется ________________________________.

8.

Если

f x′(P0 ) = f y′ (P0 ) = 0 ,

то

точка P0 (x0 , y0 )

есть

точка

экстремума

функции

z = f (x, y)

при условии ___________________.

9.

Координаты

вектора

нормали

касательной

плоскости

к

поверхности

S : F(x, y, z) = 0

( F - дифференцируемая

функция)

в

точке P0 (x0 , y0 , z0 )

равны ________________________________.

10.

Градиент

grad f (P0)

образует

с

вектором нормали

n

к

поверхности

уровня

функции

f

угол, равный _________________.

11. Для того чтобы функция f была дифференцируемой в точке,

необходимо, чтобы ______________. Доказательство. _______________.

12. Областью определения функции двух переменных z = ln(x − 2)+ ln(y − 2) является ________________________________.

13. lim sin xy x→0 xy 2 y→0

1. 1	2. 0	3. ∞	4. -1	5. Не существует.
14. Если	z = arctg (x2 + y −3 ),		то частная	производная	z′y

73

равна _______________________________.

15.

Если

z = sin uv ,

где

u = 2x +3y ,

v =

x

,

то

частная

y

производная

z′x

равна ____________________________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

y2 − z 2 + x2 − 2xz + 2x = z ,

то

а) частные производные

z′x

и

z′y равны _________, _________;

б) дифференциал

d z

имеет

вид: ___________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией

поверхности

в

точке

P0 (1,1,1)

имеет

вид: __________________________________.

17.	Стационарной точкой для				функции z = 2xy −3x2 − 2y2 +1			является
	точка ______________________, причем					у	функции	в	этой
	точке
	1. Максимум.			2.	Минимум.		3. Нет экстремума.
18.	Если	функция		z = arccos (2x + y),		то	ее	смешанная
	производная		′′	равна ________________________________.
			z xy

74

10.

1.

Областью

определения

функции

f (x, y)

двух

переменных

x и y

называется _____________________________.

2.

Множество точек

P(x, y, z) R3

называется открытым

шаром радиуса

r

с центром

в

точке

P0 (x0 , y0 ,z0 ),

если

для

d =

(x − x0 )2 + (y − y0 )2 + (z − z0 )2

справедливо

1. d < r

2. d ≤ r

3. d = r

4. d > r

5. d ≥ r .

3.

По

определению,

функция

f (x, y)

непрерывна

в точке

P0 (x0 , y0 ),

если

lim

f (x, y) __________________________.

x→x0

y→y0

4.

Разность

f (x0 , y0 + ∆y)− f (x0 , y0 )

называется ________________.

5.

Для

дважды дифференцируемой функции

z = f (x, y) вторая частная

производная

∂

2 f

,

по

определению,

есть _________________.

∂x2

6.

Если

u = f (x, y,z) -

дифференцируемая функция переменных

x , y ,

z , причем

z = ϕ(x, y) -

дифференцируемая функция независимых

переменных

x

и

y ,

то

частная

производная

∂u

∂y

вычисляется по формуле: ______________________________.

7.

Необходимыми

условиями

дифференцируемости

функции

75

Вывод. ________________________________.

12. Областью определения функции

z = f (x, y) являются ______________________________.

8. Если	′	, y0 )=	′	(x0	, y0 )= 0		и	A =	′′	(x0	, y0 ),
	f x (x0		f y						f xx
′′	, y0 ),	C =	′′			, y0 ), то	точка	P(x0 , y0 ) будет точкой
B = f yy (x0			f xy (x0
максимума		функции				z = f (x, y)		при			выполнении

условий __________________________________.

9. Уравнение вида:	x − x0		y − y0			z − z0
		=		=
	Fx′(x0 , y0 ,z0 )		Fy′ (x0 , y0 , z0 )		Fz′(x0 , y0 ,z0 )
является ___________________________ для поверхности						S , заданной
уравнением _____________________________________.

10. Производная	∂ f	( P )	в направлении		l ,	касательном	к
	∂ l	0
поверхности	уровня		функции	f	в	точке	P0 ,
равна _______________________________.

11. При	выполнении	условий	теоремы о	дифференцируемости
неявной функции		y(x), заданной уравнением		f (x, y)= 0 , формула

вычисления производной dydx имеет вид: ______________________.

трех переменных u =ln ( − x − y − z) является __________________________________.

76

13.

lim

y − x

x→0

x

y→0

1. 1

2. ∞

3. 0

4. -1

5. Не существует.

14.

Если

z = arcsin (2xy + 3y),

то

частная

производная

z′x

равна ________________________________.

15.

Если

z = tg (u 2 − 2v),

где

u = 2x +

y ,

v = xy ,

то частная

производная

z′y

равна ________________________________.

16.

Если

функция

z(x, y)

задана

неявно

уравнением

x2 + y2 + 2yz − z 2 + y − 2z = 2 ,

то

а) частные производные

z′x

и

z′y

равны _________, ___________;

б) дифференциал dz

имеет вид: ____________________________;

в) уравнение

касательной

плоскости

к

заданной

этой

функцией поверхности в точке

P0 (1,1,1)

имеет вид: ____________.

17.

Стационарной

точкой

для

функции

z = 2x2 + 2y2 − x + y −1

является точка ____________, причем у

функции в

этой

точке

1. Максимум.

2.

Минимум.

3. Нет экстремума.

18.

Если

функция

z = arcctg (x − 3y),

то

смешанная

производная

′′

равна _________________________________.

z xy

77

3. ПАКЕТЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ТЕМАТИЧЕСКОМУ МОДУЛЮ “ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И СИСТЕМЫ”

			1.
1.	Дифференциальным уравнением		первого порядка	называется
	______________________________________.
2.	Решением	(частным решением)	дифференциального	уравнения
	′	называется _____________________________.
	y =f (x,y)

′	, y	′′	y	′
3. Порядок уравнения F( y, y		) = 0 понижается заменой вида:
равно _____________________,		y′′ равно _______________________.

4. Геометрический смысл решения задачи Коши для уравнения y′ = f (x, y)

состоит в том, что ______________________________.

5. Если	корни	характеристического			уравнения	k1 ,k2 ,k3
действительные		и такие,	что	k1 = k2 и	k1 ≠ k3 , то общее	решение
уравнения y′′′+ py′′+qy′+ry = 0				( p, q, r − const)		имеет
вид: ____________________________________.

6.	Если в уравнении	y′′ + py′ + qy = x2eαx ( p,q − const )	коэффициент α
	такой, что α2 + pα + q ≠ 0, то его частное		решение
	имеет вид: ______________________________.
7.	Если y1 , y2 , y3	являются функциями от x , то	определитель

78

Вронского имеет вид: ____________________________.

8. Согласно методу		вариации	произвольных постоянных,				если
y0 = c1y1 +c2 y2 -		общее решение уравнения			y′′+ py′+ qy = 0,		то
общее	решение	уравнения	y′′ + py′ + qy = f (x)			имеет вид: y
равно	_____________, где		c1(x)	и	c2 (x)	определяются

из системы ______________________________________.

9.Нормальная система двух дифференциальных уравнений первого порядка имеет вид: _________________________________.

10.Если p 2 −4q >0 , то линейно независимые частные решения

уравнения y′′+ py′+ qy = 0 ( p,q − const) имеют

вид: ____________________. Доказательство. _____________________.

11. По

определению,

решение

x

0

(t) = (ϕ (t),K,ϕ

n

(t))T

системы

x1 = f1(t, x1 ,..., xn );

1

&

.........................

.........................

с

начальными

данными в

точке t0

= f

(t, x

,..., x

) ,

x

&

n

n

1

n

называется

устойчивым по

Ляпунову,

если __________________.

12. Установить соответствие

79

Фазовый портрет

Характер точки покоя

1.

А. Устойчивый фокус

Б. Неустойчивый фокус

В. Устойчивый узел

Г. Неустойчивый узел

Д. Седло

Е. Центр

Ответ: 1._________.

13.

Общee решение уравнения

y′(1 + x2 )=

1 − y 2 есть _____________.

14.

′

x

y

является ______________.

+ x

Общим интегралом уравнения y = y

15.

Общим решением уравнения

y

′

y

1

является ______________.

= x

+ x2

16.

Общим интегралом

уравнения

( y − x +1) dx + (x − 2y) dy = 0

является ________________________________.

′′

x

1

′

1

y

y(0) = ln 2 2 ,

= ln 2

17.

Решением задачи

Коши

=

2

,

y (0)

является _______________________________.

18.

Общим решением уравнения

y

′′

является _________________.

+ y = 0

19.

Общим решением уравнения

y

′′

2

является _________________.

+ y = x

20.

Общим решением уравнения

y′′ + y = x2 + sin2x является __________.

80

			dy				= −z ;
21.	Общим решением системы dx							является___________________.
					dz		= y ,
			dx
22.	Если 1,	e−x - фундаментальная						система	решений
	линейного	однородного	дифференциального уравнения,						то это
	уравнение	имеет	вид: ________________________________.

		2.
1.	Линейным дифференциальным		уравнением	первого порядка
	называется уравнение	вида: ____________________________.
2.	Дифференциальное	уравнение		вида
	M1(x)M 2 (y)dx+N1(x)N2 (y) dy=0		называется ___________________.

3. Если	dU (x, y) = P(x, y) dx + Q(x, y) dy , то	общий	интеграл
дифференциального уравнения P(x, y) dx + Q (x, y) dy = 0			имеет
вид: ______________________________________.

4. Задачей	Коши	для	дифференциального	уравнения
y(n) = f (x, y, y′,..., y (n−1) )			называется ________________________.

5. Если корни характеристического уравнения k1 , k2 действительны и различны, то общее решение уравнения y′′ + py′ + qy = 0 ( p,q − const)

имеет вид:__________________________________.

81

6. Если	a + bi	не	является	корнем	уравнения
k 2 +pk+ q=0		(p , q − const),	то	частное	решение
уравнения		y′′ + py′ + qy = eax (x cos bx + sin bx)			имеет
вид: _______________________________________.

7. Если	функции y1		и y2 -	линейно	зависимы на	отрезке [a,b],
то	при	любом	x [a,b]	для	определителя	Вронского
W (y1, y2 )		верно
1. W ≤ 0		2. W ≥ 0	3. W = 0		4. W < 0	5. W > 0 .

8. Если	y*	и	y*	-	соответственно частные	решения	уравнений
	1		2
y′′ + py′ + qy = f1(x),				y′′ + py′ + qy = f2 (x) , то		сумма	y1* + y*2
есть	частное		решение		уравнения _____________________________.

		y′	= f	1	(x, y , y	2	, y	3	);
		1			1
9. Решением	системы	y2′	= f2 (x, y1 , y2 , y3 );							на	[a,b]
		y3′ = f3 (x, y1 , y2 , y3 ),

называется ___________________________________.

10. Если y1 и y2 - линейно	независимые		решения	уравнения
y"+py'+qy=0 (p,q − const),	то	его	общее решение имеет
вид: ____________________.	Доказательство. ____________________.

82

		x = a				x + a y ;
11. Для системы			&		11	12		с действительными корнями λ1 , λ2
			&
		y		= a21x + a22 y,
характеристического						уравнения			установить	соответствие
	Корни λ1,λ2			( λ1 ≠ λ2 )				Устойчивость точки покоя
	1.	λ1 < 0 ,		λ2	< 0			А.	Устойчива
	2.	λ1 > 0 ,		λ2	> 0			Б.	Асимптотически устойчива
	3.	λ1 > 0 ,		λ2	< 0			В.	Неустойчива

Ответ: 1. __________, 2. __________, 3. __________.

12. Установить соответствие

	Фазовый портрет	Характер точки покоя
		А.	Устойчивый фокус
		Б.	Неустойчивый фокус
		В.	Устойчивый узел
		Г.	Неустойчивый узел
	1.	Д.	Седло
		Е.	Центр

Ответ: 1.______________.

83

′

sinx

13.

Общим решением уравнения

y

+

= 0

является _____________.

tg y

14.

Общим интегралом уравнения

y

′

x2

y

является _____________.

= y 2

+ x

y

15.

Общим решением уравнения

y′=

+ x2

является ____________.

x

16. Общим интегралом уравнения e x−y dx + (1 − e x−y ) dy = 0

является __________________________________.

	17. Решением задачи Коши	y	′′	= sin2x,	y(0) =1,	′	= −	1
								2
						y (0)

является __________________________________.

18. Общим решением уравнения y′′− 2y′+ y = 0 является ______________.

19. Общим решением уравнения y′′ − 2y′ + y = x является ____________.

20.	Общим	решением	уравнения				y′′ − 2y′ + y = x + cos x
	является _____________________________________.
			dy			= 2y	− z ;
21.	Общим решением системы						является ______________.
			dx
			dz			= y,
			dx

84

22. Если sin2x, cos2x - фундаментальная		система	решений
линейного	однородного дифференциального уравнения,		то это
уравнение	имеет вид: ________________________________________.

3.
1. Общим интегралом дифференциального уравнения	y′ = f (x, y)
называется ________________________________.

2.Однородным дифференциальным уравнением первого порядка называется уравнение вида:______________________________.

3. Порядок уравнения F (x, y′′, y′′′)=0	понижается заменой вида:
y′′ равно _____________________, y′′′	равно ____________________.

4. Задача об отыскании частного решения дифференциального уравнения y′ = f (x, y) , удовлетворяющего заданному начальному условию ____________________, называется _____________________.

5. Если	корни характеристического уравнения			такие,	что k1,2 = a ±ib
и	k3 - действителен,	то	общее	решение	уравнения
y′′′ +	py′′ + qy′ + ry = 0	( p,q,r − const) имеет вид: _________________.

6. Если α - простой корень		уравнения	k 2 + pk + q = 0 , то частное
решение	уравнения	y′′ + py′ + qy = eαx ( p,q = const)
имеет	вид: ________________________________________.

85

7.

Если определитель

Вронского

W (y1, y2 )≠ 0

хотя бы в одной

точке

интервала

(a,b) ,

то

функции

y1

и

y2

на

интервале

(a,b) ______________________________.

8.

Если

y1,

y2

-

частные

решения

уравнения

y′′ + py′ + qy = 0

( p, q − const) ,

то

сумма

y1+y2

есть ___________________________________.

y′

= f

1

(x, y , y

2

);

9.

Общим

решением

системы

1

1

′

= f2 (x, y1 , y2 ) ,

y2

называется ____________________________.

10.

Общий

интеграл

уравнения

в

полных

дифференциалах

P(x, y) dx + Q(x, y) dy = 0

имеет

вид: __________________________.

Вывод. _________________________________.

11.

По

определению,

решение

x

0

(t) = (ϕ (t),K,ϕ

n

(t))T

системы

1

x1 = f1(t, x1 ,..., xn );

&

.........................

с начальными данными в точке t0

называется

.........................

&

= fn (t, x1 ,..., xn ) ,

xn

асимптотически

устойчивым, если _____________________________.

86

12. Установить соответствие
	Фазовый портрет			Характер точки покоя
	1.			А.	Устойчивый фокус
				Б.	Неустойчивый фокус
				В.	Устойчивый узел
				Г.	Неустойчивый узел
				Д.	Седло
				Е.	Центр

Ответ: 1. ___________.

13.

Общим решением уравнения

(1+x )yy′= 1

является ____________.

14.

Общим интегралом уравнения

′

= tg

y

y

является ____________.

x

+ x

y

15.

Общим решением уравнения

y′

=

y

− x2

является ____________.

x

16. Общим

интегралом

уравнения

(2x − y −1)dx + (2y − x)dy = 0

является ________________________________.

17.

Решением

задачи

Коши

y

′′

x

y(0)= 0,

′

=cos 2 ,

y (0)= 0

является ________________________________.

18.

Общим решением уравнения

′′

′

является __________.

y −y −6y = 0

19. Общим решением уравнения y′′−y′−6y =1 + x является ___________.

87

20.	Общим	решением	уравнения				y′′ − y′ − 6y = x +1 + sin x
	является ______________________________.
				dy		= 3y − 2z;
21.	Общим решением системы			dx			является ______________.
					dz	= 3y − 4z,
				dx

22. Если	1, x	- фундаментальная	система	решений		линейного
однородного		дифференциального	уравнения,	то	это	уравнение
имеет	вид: ________________________________________________.

4.

1. Дифференциальное

уравнение

первого порядка, разрешенное

относительно производной, имеет вид: _____________________.

2.Дифференциальное

уравнение

вида

y′+ P(x)y = Q(x)

называется ___________________________________.

3. Общий интеграл дифференциального уравнения	y′′ = f (x) имеет
вид: _________________________________________.

4.Теорема о существовании и единственности решения задачи Коши для дифференциального уравнения y′ = f (x, y) формулируется следующим

образом: ________________________________________.

88

5.	Для	дифференциального		уравнения	y′′′+ py′′+ qy′+ ry = 0
	(p,q,r − const)		характеристическое		уравнение		имеет
	вид: _________________________________________.
6.	Если	a +bi является корнем уравнения			k 2 + pk + q = 0	,	то частное
	решение уравнения		y′′ + py′ + qy = eax (cos bx + x sin bx) ( p,q − const)
	имеет	вид: _________________________________.

7.Если функции y1 и y2 - линейно зависимы на отрезке [a,b], то при

любом x [a, b] определитель Вронского W (y1, y2 ) _____________.

8. Если y1, y2 - фундаментальная система решений уравнения

y′′+ py′+ qy = 0

( p,q − const) ,

а

C1′(x) и

C2′ (x)

есть

C′

y

+ C′

y

2

= 0;

решение

системы

1

1

2

то

общее

решение

′

′

′

′

f (x),

C1 y1

+ C2 y

2

=

уравнения

y′′+ py′+ qy = f (x)

имеет

вид: ___________________.

9. Нормальная		система	трех	дифференциальных	уравнений
имеет	вид: ________________________________________.

10. Если	y1 и	y2 -	частные		решения	уравнения
y′′+ py′+ qy = 0		(p, q−const ),		то	сумма	y1 +y2
есть __________________.			Доказательство. _____________________.

89

x = a11x +a12 y ;

11.

Для системы

&

с действительными корнями λ1 , λ2

y = a21x + a22 y ,

&

характеристического

уравнения

установить

соответствие

Корни

λ1 , λ2

Характер точки покоя

А.

Устойчивый фокус

1. λ1 < 0,

λ2 < 0

Б.

Неустойчивый фокус

2. λ1 > 0 ,

λ2 > 0

В.

Устойчивый узел

3. λ1 > 0 ,

λ2 < 0

Г.

Неустойчивый узел

Д.

Седло

Е.

Центр

Ответ: 1. _______,

2. _______,

3. _______.

12.

Установить соответствие

Фазовый портрет

Характер точки покоя

1.

А.

Устойчивый фокус

Б.

Неустойчивый фокус

В.

Устойчивый узел

Г.

Неустойчивый узел

Д.

Седло

Е.

Центр

Ответ. 1. __________.

90

13. Общим решением уравнения y′− xe y = 0 является ______________ .

14.

Общим интегралом уравнения

y

′

y

y

= sin x + x

является ___________.

y

15.

Общим решением уравнения

y′

=

+ x3

является ______________.

x

16.

Общим

интегралом

уравнения

(2 −3xy2 )dx −3x2 ydy = 0

является __________________________________.

17.

Решением

задачи

Коши

y

′′

= e

−x

,

y(0)= 0 ,

′

y (0)= −1

является __________________________________.

18.

Общим решением уравнения

y′′+ 2y′+ y = 0

является __________.

19.

Общим решением уравнения

y′′ + 2y′ + y = cos 2x является ________.

20.

Общим

решением

уравнения

y′′ + 2y′ + y = cos 2x + x

является __________________________________.

dy

= −z ;

21.

Общим решением системы

dx

является _____________.

dz

= y − 2z ,

dx

22.

Если

sin x , cos x

-

фундаментальная

система

решений

линейного

однородного

дифференциального

уравнения,

то

это уравнение имеет вид: ____________________________________.

91

		5.
1. Уравнение	вида	f (x, y, y′, y′′)= 0	называется ___________

порядка _____________________________________.

2.Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: ____________________________________.

	y′ =	y
3. Дифференциальное уравнение вида		f		преобразуется в
		x

дифференциальное уравнение с разделяющимися переменными с помощью замены ___________________________________________.

4.

Геометрический

смысл

решения

задачи

Коши

для

дифференциального

уравнения

y′′ = f (x, y, y′)

состоит в том,

что ______________________________________.

5.

Для

дифференциального

уравнения

y′′+ py′+ qy = 0

(p,q − const)

характеристическое уравнение имеет вид: ________________________.

6.

Если

α

- кратный

корень уравнения

k 2 + pk + q = 0 ,

то

частное

решение

уравнения

y′′+ py′+ qy = xeαx

(p,q − const)

имеет

вид: ____________________________________.

7.Если определитель Вронского W ( y1 , y2 ) ≡ 0 на интервале (a,b), то

функции y1, y2 на (a,b) _______________________________.

8. Если y1 и	y2 - линейно	независимые решения уравнения
y′′+ py′+ qy = 0	(p,q − const),	то его общее решение имеет

вид: _______________________________________.

92

9. Задачей

Коши

для

системы

называется ____________________________.

y′ =	f	1	(x, y		, y	2	, y	3	);
1				1
y2′ = f2				(x, y1, y2 , y3 );
				(x, y1, y2 , y3 ),
y3′ = f3

10.Согласно методу вариации произвольной постоянной, общее решение

уравнения y′′ + py′ + qy = f (x) (p,q − const) имеет вид:

___________________. Доказательство. _____________________.

x1 = f1(t, x1,..., xn );

&

...........................

11.

По определению, точкой покоя

системы

..........

.................

= f

(t, x ,..., x

) ,

x

&

n

n

1

n

называется ______________________________.

12.

Установить соответствие

Фазовый портрет

Характер точки покоя

А.

Устойчивый фокус

Б.

Неустойчивый фокус

В.

Устойчивый узел

Г.

Неустойчивый узел

Д.

Седло

1.

Е.

Центр

Ответ: 1. ___________.

93

13.

Общим

интегралом

уравнения

1− x2 dy + (1+ y2 )dx = 0

является ___________________________.

14.

y

′

y

y

Общим интегралом уравнения

= cos x + x

является _________.

15.

Общим решением уравнения

y

′

y

1

является ___________.

= x

− x2

16.

Общим

интегралом

уравнения

(y − 2x + 2)dx + (y + x)dy = 0

является ________________________________.

17.

Решением

задачи

Коши

y

′′

=

3x

2

+e

x

,

y(0) = 0,

′

y (0) =1

является _________________________________.

18.

Общим решением уравнения

y′′+ 4y = 0

является ______________.

19.

Общим решением уравнения

y′′+ 4y = 4x2

является ___________.

20.

Общим

решением

уравнения

y′′ + 4y = 4x2 + sin 3x

является ________________________________.

dy

= z ;

21.

Общим решением

системы

dx

является ______________.

dz

= −4y ,

dx

22. Если ex , e−x - фундаментальная система решений линейного однородного дифференциального уравнения, то это уравнение имеет вид :____________________________________.

94

6.

1.

Интегралом

(частным

интегралом)

дифференциального уравнения

y′ = f (x, y)

называется _____________________________________.

dy

y

2.

Дифференциальное

уравнение

вида

=

f

dx

называется ____________________________.

x

3.

Порядок уравнения

′

, y

′′

понижается

заменой

y

′

F( y, y

) = 0

равно _____________________, y′′ равно ______________________.

4. Задача об отыскании частного решения дифференциального уравнения y′′ = f (x, y, y′) , удовлетворяющего заданным начальным условиям

___________________, называется ______________________.

5.

Если корни характеристического уравнения

k1

и k2

действительны и

равны

(k1 = k2 ) ,

то

общее

решение

уравнения

y′′ + py′ + qy = 0

( p,q − const)

имеет

вид: __________________________________.

6.

Если

a + ib

является

корнем уравнения

k 2 + pk + q = 0 , то

частное

решение

уравнения

y′′ + py′ + qy = eax x cos bx

( p, q − const)

имеет

вид: __________________________________.

7.

Если

для решений

y1(x),

y2(x),

x [a,b]

уравнения

y′′ + py′ + qy = 0

(p,q

–

const)

определитель

Вронского

W(x0)=0,

(x0 [a,

b]), то

функции y1, y2 ________________________________.

8.

Систему

y′

= f

1

(x, y , y

2

);

можно

свести к дифференциальному

1

1

′

= f2 (x, y1 , y2 ) ,

y2

уравнению вида: _________________, порядка ____________________.

95

9.	Если y1 - частное решение уравнения y′′ + py′ + qy = 0 ( p,q − const) ,
	то Ay1	(A − const) есть _____________________________________.
10.	Общее	решение уравнения	y′ + P(x) y = Q(x)	( P(x) и Q(x) -

непрерывные на (a,b) функции) имеет вид: _____________________.

Вывод. _________________________________.

x= a11x+ a12y;

11. Для системы

&

с

комплексными корнями λ1,λ2

y = a21x +a22y,

&

характеристического

уравнения

установить

соответствие

Корниλ1 = α + iβ, λ2 = α − iβ

Характер точки покоя

1.

α < 0, β ≠ 0

А.

Устойчивый фокус

Б.

Неустойчивый фокус

2.

α > 0, β ≠ 0

В.

Устойчивый узел

Г.

Неустойчивый узел

3.

α = 0, β ≠ 0

Д.

Седло

Е.

Центр

Ответ: 1._____, 2._____, 3._____.

12. Установить соответствие

Характер точки покоя

Фазовый

портрет

А.

Устойчивый фокус

Б.

Неустойчивый фокус

В.

Устойчивый узел

Г.

Неустойчивый узел

Д.

Седло

1.

Е.

Центр

Ответ: 1._________.

96

13.

Общим

интегралом

уравнения

(1 + x2 )dy + 2 y dx = 0

является ______________________.

y

y

14.

Общим интегралом уравнения

y

′

= e

x

является ______________.

+ x

15.

Общим решением уравнения

x′ =

x

1

является _______________.

−

y

y 2

16.

Общим

интегралом

уравнения

(ye x −1)dx + e x dy = 0

является ______________________.

17.

′′

′

= 0 ,

y(1) =

1

′

2 ,

является

Решением задачи Коши y x − y

y (1) =1

______________________.

18.

Общим решением уравнения

y′′ − 2y′ − 3y = 0

является ____________.

19.

Общим решением уравнения

y′′ − 2y′ − 3y = e x

является ___________.

20.

Общим

решением

уравнения

y′′ − 2y′ − 3y = e x + cos3x

является ______________________.

dy

= 4y − 5z ;

21.

Общим

решением

системы

dx

является _________.

dz

= y − 2z ,

dx

21.Если 1, e2x - фундаментальная система решений линейного однородного дифференциального уравнения, то это уравнение имеет вид: ___________________________.

97

						7.
1.	Общим решением				дифференциального			уравнения	y′ = f (x, y)
	называется _____________________________.
2.	Уравнением		Бернулли			называется	дифференциальное		уравнение
	вида: ___________________________________.
3.	Общий		интеграл			дифференциального			уравнения
	M1(x)M 2 ( y)dx + N1(x)N2 ( y)dy = 0						имеет вид: ________________.
4.	Задачей Коши для дифференциального уравнения								y′ = f (x, y)
	называется ______________________________.
5.	Если	корни	характеристического уравнения k1,k2 ,k3 действительны и
	различны,		то	общее		решение	уравнения y′′′+ py′′+ qy′+ ry = 0
	( p,q,r − const)			имеет		вид: _________________________________.
6.	Если	α - простой корень уравнения k 2 + pk + q = 0 , то частное решение
	уравнения			y′′+ py′+ qy = x2eαx			( p,q − const)		имеет
	вид: _____________________________________.
7.	Если	y1, y2		-	фундаментальная		система	решений	уравнения
	y′′+ py′+ qy = 0			( p,q − const) , а C1′(x) и C2′(x)				есть решение системы

	′	y1	′	y2 =
C1			+ C2
	′	′	′	′
					=
C1		y1	+ C2	y2

0;

f (x) ,

то y = C1(x) y1 + C2 (x) y2 является общим

решением уравнения _______________________.

98

8. Если решения	y1 , y2	уравнения	y′′+ py′+ qy = 0	линейно
независимы на	[a,b],	то для любого x [a,b] определитель
Вронского W (x) ________________________________.

9.Решением

[a,b]

		y′		= f	1	(x, y , y	2	);
	системы		1			1			на
			′	= f2 (x, y1 , y2 ) ,
		y2

называется ____________________________.

10.		Если	y0 - общее решение				уравнения		y′′+ py′+ qy = 0 ( p,q − const) ,
		y -	частное	решение	уравнения y′′ + py′ + qy = f (x) , то общее
		решение неоднородного уравнения имеет вид: ___________________.
	Доказательство. ___________________________________.
					x1 = f1(t, x1 ,..., xn );
							&
11.	По определению система				..........................					имеет устойчивую
					..........................
							&		,..., xn ) ,
					xn = fn (t, x1
	точку		покоя,	если _______________________________.
12.	Установить соответствие
			Фазовый портрет					Характер точки покоя
								А.	Устойчивый фокус
								Б.	Неустойчивый фокус
								В.	Устойчивый узел
								Г.	Неустойчивый узел
								Д.	Седло
		1.						Е.	Центр
		Ответ: 1.__________.

99

13.

Общим

интегралом

уравнения

xe y dx − (2 + x2 )dy = 0

является _______________________.

14.

y

′

y

y

Общим интегралом уравнения

= ctg x + x

является __________.

15.

Общим решением уравнения

x′ =

x

2

является _____________.

+

y

y3

16.

Общим

интегралом

уравнения

(2x + y − 2)dx + (x + 2y)dy = 0

является

________________________.

17.

Решением задачи Коши

y′′tgx − y′ = 0 ,

π

=1,

π

является

y

y′

=1

________________________.

2

2

18.

Общим

решением

уравнения

y′′+9y = 0

является ________.

19.

Общим

решением

уравнения

y′′+9y = 9x2

является ________.

20.

Общим

решением

уравнения

y′′ + 9y = 9x2 + sin x

является ______________________________.

dy

= −9z ;

21.

Общим

решением

системы

dx

является _____________.

dz

= y ,

dx

22. Если

e x , e−2x -

фундаментальная

система

решений

линейного

однородного

дифференциального

уравнения,

то это уравнение

имеет

вид: ___________________________.

100

8.

1. Уравнение вида f (x, y, y′) = 0 называется_________ порядка _________.

2.

Если

∂ P

=

∂Q

,

то

дифференциальное

уравнение

вида

∂ y

∂ x

P(x, y ) dx+Q(x, y) dy = 0

является ___________________________.

3.

Дифференциальное

уравнение

вида

y′ + P(x)y = Q(x)

интегрируется

подстановкой __________________________________.

4.

Теорема о существовании и единственности решения

задачи Коши для

дифференциального

уравнения

y

′′

′

формулируется

= f (x, y, y )

следующим образом: ___________________________.

5.

Если корни характеристического уравнения такие, что

k1,2 = a ±ib , то

общее

решение

уравнения

y′′+ py′+ qy = 0 ( p,q − const)

имеет вид: ____________________________________.

6.

Если

a +ib

корень

уравнения

k 2 + pk + q = 0,

то

частное решение

уравнения

y′′ + py′ + qy = eax x sin bx

( p,q − const)

имеет вид: _______.

7.

Если

для

решений

y1(x), y2 (x)

(x [a,b])

уравнения

y′′+ py′+ qy = 0

( p,q − const)

определитель

Вронского

W (x0 )≠ 0

(x0 [a,b]),

то

функции

y1 ,

y2 ______________________________.

8.

Согласно

принципу

суперпозиции,

частное

решение

y

уравнения

y′′ + py′ + qy = f1(x) + f2 (x)

( p,q − const)

представимо

в

виде

суммы ___________________,

где

слагаемые - частные

решения

уравнений ______________________,

___________________________.

101

9. Если в уравнении y′′ + py′ + qy = Pn (x)eax								( p,q − const , a2 + pa + q ≠ 0)
P (x) - многочлен				n-й	степени,		то частное решение y имеет
n
вид: _______________________. Вывод. __________________________.
			x= a11x + a12 y ;
10. Для системы				&			с действительными		корнями λ1 ,λ2
			y = a21x + a22 y ,
				&
характеристического					уравнения			установить	соответствие
	Корни λ1 ,λ2			(λ1 = λ2 = λ)			Характер точки покоя
	1.						А.	Устойчивый фокус
			λ > 0				Б.	Неустойчивый фокус
							В.	Устойчивый узел
							Г.	Неустойчивый узел
	2.		λ < 0				Д.	Седло
							Е.	Центр
Ответ: 1._______, 2.________.
11. Установить соответствие
		Фазовый		портрет			Характер точки		покоя
	1.						А.	Устойчивый фокус
							Б.	Неустойчивый фокус
							В.	Устойчивый узел
							Г.	Неустойчивый узел
							Д.	Седло
							Е.	Центр

Ответ: 1. ___________.

102

y′

=

f

1

(x, y , y

2

) ;

называется __________.

12. Задачей Коши для системы

1

1

′

= f2 (x, y1 , y2 ) ,

y2

13.

Общим интегралом уравнения

y′ = 2x+ y

является ________________.

14.

y

′

x

y

Общим интегралом уравнения

=

y

+ x является ______________.

15.

Общим решением уравнения

x′ =

x

1

является ______________.

−

y

y 4

16.

Общий интеграл уравнения

(y 2 − 2x)dx + 2xy dy = 0

есть ___________.

17.

Решением задачи

Коши

′′

+ y

′

= 0,

′

y ctg x

y(0) =1, y (0) =1

является __________________.

18.

Общим решением уравнения

y′′+ 4y′+ 4y = 0

является ____________.

19.

Общим решением уравнения y′′+ 4y′+ 4y = e2x является ____________.

20.

Общим решением

уравнения

y′′ + 4y′ + 4y = e2x + cos2x

является ___________________.

dy

= −z ;

21.

Общим решением системы

dx

является ______________.

dz

= 4y − 4z ,

dx

22. Если sin3x, cos3x - фундаментальная система решений линейного однородного дифференциального уравнения, то это уравнение имеет вид:___________________________________.

103

9.

1.Дифференциальное уравнение второго порядка, разрешенное относительно второй производной, имеет вид: ___________________.

2.

Дифференциальное уравнение вида y′ + P(x) y = y αQ(x) ,

где

α

- любое

вещественное число, называется ____________________.

3.

Порядок

уравнения

′

′′

понижается заменой

вида:

F(x, y

, y ) = 0

y′ равно ____________________,

y′′

равно ___________________.

4.

Задачей

Коши для

дифференциального

уравнения

y

′′

′

= f (x, y, y )

называется __________________________________.

5.

Если

корни

характеристического

уравнения

k1 ,k2 ,k3 действительны

и

равны

(k1 = k2 = k3 ),

то

общее

решение

уравнения

y′′′ + py′′ + qy + r = 0 ( p,q,r − const)

имеет

вид: _________________.

6.

Если

α

- кратный корень уравнения

k 2 + pk + q = 0 ,

то частное

решение

уравнения

y′′+ py′+ qy = x2eαx

( p,q − const)

имеет

вид: ________________________________.

7.Если y1 , y2 являются функциями от x , то определитель Вронского имеет вид: ________________________________.

8.Если y0 - общее решение уравнения y′′+ py′+ qy = 0 ( p,q − const) , y -

частное решение уравнения y′′ + py′ + qy = f (x) , то общее решение

неоднородного уравнения имеет вид: __________________________.

104

y′

= f

1

(x, y , y

2

, y

3

) ;

1

1

9.

Общим

решением

системы

y2′

= f2

(x, y1 , y2 , y3 ) ;

(x, y1 , y2 , y3 ) ,

y3′ = f3

называется _____________________________.

10. Если функции y1 и y2 - линейно

зависимы на отрезке [a,b], то

определитель

Вронского

на

этом отрезке

__________________.

Доказательство. ________________________________.

x= a11x+ a12 y ;

11.

Для системы

&

с

комплексными

корнями λ1, λ2

y = a21x + a22 y ,

&

характеристического

уравнения

установить

соответствие

Корни λ1 = α + iβ, λ2 = α − iβ

Устойчивость точки покоя

1.

α < 0, β ≠ 0

А. Устойчива

2.

α > 0 , β ≠ 0

Б. Асимптотически устойчива

3.

α = 0 , β ≠ 0

В. Неустойчива

Ответ: 1. ________, 2. _______, 3. _______.

12.

Установить соответствие

Фазовый портрет

Характер точки покоя

А.

Устойчивый фокус

Б.

Неустойчивый фокус

В.

Устойчивый узел

Г.

Неустойчивый узел

Д.

Седло

1.

Е.

Центр

Ответ: 1._______.

105

13.

Общим интегралом уравнения

e2x−y y′ =1

является _____________.

y

y

14.

Общим интегралом уравнения

y

′

= 2

x

является _____________.

+ x

15.

Общим решением уравнения

x′ = xy −

y

является _______________.

16.

Общим

интегралом

уравнения

(y2 + x2 )dx + 2xydy = 0

является _________________________.

17.

Решением

задачи Коши

′′

′

=

0 ,

π

′

π

y sin x − y

y

= ln ( 2 ),

y

=1

2

2

является __________________________________.

18.

Общим решением уравнения

y′′+ 25y = 0

является ______________.

19.

Общим решением уравнения

y′′+ 25y = 26ex

является ___________.

20.

Общим

решением

уравнения

y′′ + 25y = 26e x + 25x

является __________________________________.

dy

= z ;

21.

Общим

решением

системы

dx

является

dz

= −25y ,

dx

______________.

22.Если 2 , 3x - фундаментальная система решений линейного однородного дифференциального уравнения, то это уравнение имеет вид: _____________________________________.

106

10. 1. Общим интегралом дифференциального уравнения второго порядка

f (x, y, y′, y′′) = 0 называется __________________________________.

2.Дифференциальным уравнением в полных дифференциалах называется уравнение вида: ____________________, если ____________________.

3.	Дифференциальное		уравнение	вида	y′ + P(x) y = y nQ(x)
	интегрируется	подстановкой _________________________________.
4.	Задачей Коши	для	дифференциального		уравнения y	′′′	′	, y	′′
							= f (x, y, y		)

называется ___________________________________.

5.Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид: _____________.

6.

Если

a +ib является корнем уравнения k 2 + pk + q = 0 ,

то частное

решение

уравнения

y′′ + py′ + qy = eax cos bx;

( p,q − const) имеет

вид :_________________________________________.

7.

Если

решения

y1,

y2

уравнения

y′′+ py′+ qy = 0

линейно

зависимы на [a;b], то определитель Вронского

W (x)

для любого

x [a;b] _____________________________________.

y′ = f

1

(x, y

, y

2

, y

3

);

1

1

8.

Систему

y2′ = f2 (x,

y1, y2 , y3 );

можно

свести к

дифферен-

y1, y2 , y3 ) ,

y3′ = f3 (x,

9.

циальному

уравнению

вида: _______________ порядка __________.

По

определению,

фундаментальной системой

решений

уравнения

y′′′+ py′′+ qy′+ ry = 0 ( p,q,r − const) называется _________________.

107

10.

Если в

уравнении

y′′ + py′ + qy = Pn (x)eax ,

( p,q − const ,

a - простой

корень

уравнения

k 2 + pk + q = 0),

P (x) −

n

многочлен

n-й

степени,

то частное решение

y*

имеет

вид: _____________________. Вывод. __________________________.

x= a11x+ a12 y;

11.

Для системы

&

с действительными корнями λ1, λ2

y = a21x + a22 y,

&

характеристического

уравнения

установить

соответствие

Корни λ1 ,λ2

(λ1 = λ2 = λ)

Устойчивость точки покоя

1. λ> 0

А. Устойчива

Б. Асимптотически устойчива

2. λ < 0

В. Неустойчива

Ответ: 1. ______,

2. ______.

12. Установить соответствие

Фазовый портрет

Характер точки покоя

1.

А.

Устойчивый фокус

Б.

Неустойчивый фокус

В.

Устойчивый узел

Г.

Неустойчивый узел

Д.

Седло

Е.

Центр

Ответ: 1.________.

13.

Общим решением уравнения

(1 + x) y′ = e y является __________.

108

	14.	Общий интеграл уравнения		y	′		y		y	есть _________________.
						= x			+ x
	15.	Общим решением уравнения			x′ =		x	− y3		является _____________.
							y
	16.	Общим	интегралом	уравнения						2xydx +(x2 − 2y)dy = 0
		является ______________________________.

17. Решением задачи	Коши	x	2	y	′′	+ 2xy	′	= 0, y(1)	= 0,	′	=1
										y (1)

является ______________________________.

18.	Общее	решение	уравнения	y′′−5y′+6y = 0	есть ________________.
19.	Общее	решение	уравнения	y′′−5y′+6y = x	есть ________________.

20. Общим решением уравнения y′′ − 5y′ + 6y = x + sin 2x

является ______________________________.

	dy			= 4y + z;
21. Общим решением системы	dx			является _____________.
	dz			= −2y + z,
	dx

22. Если 3,	ex - фундаментальная		система	решений линейного
однородного	уравнения,	то	это	уравнение	имеет
вид: ____________________________________.

109

4. ПАКЕТЫ ТЕСТОВЫХ ЗАДАНИЙ ПО ТЕМАТИЧЕСКОМУ МОДУЛЮ “ДВОЙНЫЕ, ТРОЙНЫЕ, КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ”

1.

1. Двойным интегралом от функции f (x, y) , непрерывной в замкнутой области G R2 , называется ________________________________.

2.

Если

функции

f (x, y)

и

g(x, y)

интегрируемы

на

G ,

f (x, y) ≤ g(x, y)

на G

и

∫∫fdG = A,

а

∫∫gdG = B ,

то

G

G

1. A > B

2. A ≤ B

3. A ≥ B

4. A < B

5. A = B .

3.

По

свойству

линейности,

если

функции

f (x, y, z) и

g(x, y, z)

интегрируемы

на

V ,

то

для

любых

чисел

A и

B

интеграл

∫∫∫(Af + Bg) dV

равен ______________________________________.

V

4.

Если

формулы

x = x(u,v,w),

y = y(u,v,w),

z = z(u,v,w)

задают

взаимно однозначное, непрерывно дифференцируемое

отображение

области

T

пространства

переменных u, v, w

на

область

Ω

пространства

переменных

x, y, z ,

то

якобиан

отображения

I (u,v,w)

равен ____________________________________.

110

5.

Если

функция

f (x, y) - неотрицательна и интегрируема

в области

G ,

то

геометрический

смысл

интеграла

∫∫ f (x, y)dxdy есть _________________________________.

G

6.

По определению,

криволинейным

интегралом

первого

рода

от

функции

f (x, y) , непрерывной

на кусочно-гладкой

кривой

AB ,

называется _________________,

его

обозначение ______________.

7.

Масса

тела

V R3

с

плотностью

ρ(x, y, z),

(x, y, z) V ,

равна ______________________________.

8.

Если

P(x,y)

и

Q(x,y)

- непрерывные

функции

на

кусочно-

гладкой

ориентированной

кривой

x = ϕ(t);

t1 ≤ t ≤ t2 ,

то

AB :

y = ψ(t) ,

∫P(x, y) dx + Q(x, y) dy

вычисляется

по формуле: _______________.

AB

9.

Статический момент

M OY

относительно

оси

OY

кусочно-гладкой

кривой AB с плотностью ρ(x, y) вычисляется по формуле: ___________.

10.

Для

функций

P(x,y)

и

Q(x, y) ,

непрерывных

вместе с

производными

∂P

и

∂Q

в

замкнутой области G , ограниченной

∂y

∂x

кусочно-гладкой

ориентированной

кривой

L ,

формула

Грина

имеет

вид: _______________________________.

11. Потоком

вектора

F

(x, y, z) = P(x, y, z)i

+ Q(x, y, z) j + R(x, y, z)k

через

кусочно-гладкую

ориентированную

поверхность

S

111

называется _______________________________________.

12. Если функции	P(x, y, z),	Q(x, y, z),	R(x, y, z)		непрерывны	на
кусочно-гладкой	ориентированной		поверхности		S с вектором
нормали nr (cos α, cosβ, cos γ),		то ∫∫(P cos α + Q cosβ + R cos γ)ds				через
		s
поверхностный	интеграл	второго		рода	представляется

в виде: ___________________________________.

13. Двукратный интеграл для	∫∫ f (x, y) dxdy по области D , ограничен-
	D
ной кривыми: x + y = 2,	y = 4 − x2 , имеет вид: _______________.

1	2−y
14. Изменение порядка интегрирования в интеграле ∫dy	∫ f (x, y)dx
0	y2

приводит его к виду:______________________________________.

15. Интеграл

∫∫

dxdy

по

области

D ={(x, y) :1 ≤

x 2 + y 2 ≤ 2},

x

2 2

D

+ y

вычисленный

в

полярных

координатах,

равен

1. πln2

2. ln2

3. 2πln2

4.

−

3π

5. π.

2

16. Расстановка

пределов

интегрирования

в

∫∫∫f (x, y, z) dxdydz

V

по

области

V ,

ограниченной

поверхностями:

y = x2 ,

x = y2 ,

z = xy,

z = 0 , приводит

к

кратному интегралу

112

вида: ______________________________________.

17.

Масса

тела

V ={(x, y, z) :

x > y > x2 ,

0 < z < xy}

с

плотностью

ρ(x, y, z) =

20

равна

x

1.

1

2.

2

3.

3

4.

4

5.

5 .

18.

Если

тело

V

ограничено

поверхностями

x2 + y 2 + z 2 =1,

z 2 = x2 + y 2 ,

причем

z ≥ 0

и

z 2 ≥ x2 + y 2 ,

то его

объем,

вычисленный

в

сферических

координатах,

равен

1.

2 +

2 π

2.

2 − 2

π

3

3

3.

2π

4.

2π

.

3

3

∫3ydl ,

AB : y 2 = 2x,

3

19. Интеграл

где

A (0;0), B (2

;

3) ,

равен

AB

1. 7

2. 8

3. 3

4. 6

5. 5 .

20. Интеграл

ydx − xdy

,

где

L :

x

= a cos t;

0

≤ t ≤ 2π,

равен

L∫

x2 + y 2

y

= a sin t ,

1. −2π

2. 2π

3. π

4. −π

5. 4π.

113

2.

1.

С

помощью

двойного

интеграла

объем

тела

V ={(x, y, z) : f (x, y) ≤ z ≤ 0 , (x, y) G}

записывается

в

виде: _____________________________.

2.

По

теореме о сведении двойного интеграла к повторному,

если функция

f (x, y) интегрируема на G ,

где

G ={(x, y) :ϕ(x) ≤ y ≤ ψ(x), a ≤ x ≤ b},

то

∫∫ f (x, y) dG равен _____________________________.

G

3.

По

свойству

аддитивности,

если

области

V , V1 и V2

такие,

что

и

функция

f (x, y, z)

интегрируема

на V ,

то

V1 V , V2 =V \V1 ,

f _________ на V1

и V2 , причем

∫∫∫f (x, y, z)dV равен _________.

V

4.

Если отображение области D плоскости переменных (r,ϕ)

на область

G

плоскости переменных (x, y) определяется полярными

координатами

r

и ϕ, то

∫∫ f (x, y) dxdy =∫∫

__________________.

G

D

5.

Статический

момент

M ox

относительно

оси

OX

пластинки

G , с

плотностью ρ(x, y), (x, y) G,

равен ___________________________.

6.

Согласно геометрическому смыслу тройного интеграла,

объем области

V R3 вычисляется по

формуле: ______________________________.

7.

По определению

криволинейным

интегралом

второго

рода

от

вектор-функции

F

непрерывной

на

(x, y) = P(x, y)i

+ Q(x, y) j ,

ориентированной

кусочно-гладкой

кривой

AB , называется

_______________,

его обозначение ___________________.

114

8. Если f (x,y) - непрерывная функция на кусочно-гладкой кривой

AB : y = y(x) (a ≤x≤ b ), то ∫ f (x, y)dl вычисляется по

AB

формуле: _________________________________.

9.Момент инерции относительно начала координат кусочно-гладкой кривой AB с плотностью ρ(x, y) вычисляется по формуле: __________.

10.

Если

P(x, y)

и

Q(x, y) - непрерывные функции в односвязной области

G и

∫P(x, y)dx + Q(x, y)dy = 0

( L -произвольный

ориентированный

L

замкнутый

контур из G ), то для любых точек

A

и

B из G

интеграл

∫P(x, y)dx + Q(x, y)dy _________________.

AB

11.

По определению, если функция

f (x, y, z)

непрерывна на кусочно-

гладкой поверхности S , то поверхностным интегралом первого рода

называется _______________, его

обозначение ___________________.

12.

По

формуле

Стокса,

циркуляция

вектора

F

по

ориенти-

(x, y, z) = P(x, y, z)i

+ Q(x, y, z) j + R(x, y, z) k

рованной

кусочно-гладкой замкнутой

кривой Γ,

являющейся краем

поверхности

S , равна ________________, где ___________________.

13.

Двукратный интеграл для

∫∫ f (x, y)dxdy

по

области D ,

ограниченной

y = x2 ,

D

кривыми:

y = x,

имеет

вид: _________________________.

1

x2

14.

Изменение

порядка интегрирования в

интеграле

∫dx ∫ f (x, y)dy

0

−x

приводит его к виду: ________________________________________.

115

15.	Интеграл	∫∫ x2 + y 2 dxdy		по	области D = {(x, y) : x 2 + y 2 ≤ 9 },
		D
	вычисленный	в	полярных		координатах,	равен
	1. 18π	2. 9π		3. 2π	4. 36π	5. 3π.
16.	Расстановка пределов		интегрирования		в ∫∫∫f (x, y, z) dxdydz	по

V

области

V ,

ограниченной

поверхностями:

2x + y = 2,

x + y =1,

x = z, x = 0, z = 0,

приводит

к

кратному

интегралу вида: _____________________________________.

17.

Масса

тела

V ={(x, y, z) : y >1 − x, y < 2 − 2x, x > 0, 0 < z < x}

с

плотностью

ρ(x, y, z) =12x

равна

1. 1

2. 2

3. 1,5

4. 0,5

5. 2,5.

18.

Если

тело

V

ограничено

поверхностями x2 + y2 +z2 =1,

z =

1

, причем

2

1

z ≥

,

то

его

объем,

вычисленный в

цилиндрических

координатах,

2

равен

1.

11π

2.

5π

3.

11π

4.

5π

5.

5π

.

48

6

24

24

12

3z 2

x = a cos t ;

19.

Интеграл

∫

dl ,

0 ≤ t ≤ 2р,

равен

2(x2 + y 2 )

где L : y = a sin t ;

L

z = a t,

1. 4a2π3	2. 8aπ2	3. 8aπ3	4. 8a2π3	5. 4aπ3 .
20. Интеграл	∫15(x2 − y 2 )dx ,	где AB : y = x 2 , A (0;0), B (2;4) ,			равен
1. 40	AB	3. − 56	4. 56		5. − 40 .
	2. −96

116

,

3.

1.

Если

функция

ρ(x, y),

((x, y) G) -

плотность

распределения масс, то

физический

смысл

интеграла

∫∫ρ(x, y) dxdy

есть__________.

G

2.

По

свойству

линейности,

если

функции

f (x, y)

и g(x, y)

интегрируемы

на

G ,

тогда

для

любых чисел

A и B

сумма

A∫∫ f dG + B∫∫g dG равна________________________________.

G

G

3.

По

свойству

монотонности

тройного

интеграла,

если

функции

f (x, y, z)

и

g(x, y, z)

интегрируемы на

V

и

f (x, y, z) ≤ g(x, y, z)

на

V ,

то ___________________________________.

4.

Якобиан J (r,

ϕ, θ)

отображения,

определяемого

сферическими

координатами

r, ϕ, θ, равен определителю_____________________.

5.

Геометрический

смысл

∫∫dx dy

есть_________________________.

G

6.

Статический момент

M XY

относительно плоскости

XOY

тела V R3 с

плотностью

ρ(x, y, z),

((x, y, z) V )

равен__________________.

7.Физический смысл криволинейного интеграла первого рода есть_______________________________.

117

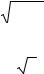
8.

Если P(x, y) и

Q(x, y) - непрерывные функции

на кусочно-гладкой

ориентированной

кривой

AB : y = f (x)

(a ≤ x ≤ b) ,

то

∫P(x, y) dx + Q(x, y) dy

вычисляется по формуле:_________________.

AB

9.

Момент инерции

JOY

относительно оси OY кусочно-гладкой кривой

AB с плотностью ρ(x, y) вычисляется по формуле:_______________.

10.

С

помощью

криволинейного

интеграла

площадь

области

G ,

ограниченной

кусочно-гладкой

ориентированной

кривой

L ,

вычисляется по

формуле:_____________________________________.

11.

По

определению,

если

вектор - функция

(x,y,z) =

F

непрерывна

на

кусочно-гладкой

= P(x,y,z) i

+ Q(x,y,z) j + R(x,y,z) k

ориентированной поверхности S , то поверхностным интегралом

второго рода называется _____________, его обозначение__________.

12.Формула Остроградского - Гаусса в векторной форме имеет вид:______________________________, где ______________________.

13.	Двукратный	интеграл для ∫∫ f (x, y) dxdy			по области D , ограниченной
			D
	кривыми	y = −x,	y = −x2 , имеет	вид:_____________________.
					1	1−x2
14.	Изменение	порядка	интегрирования	в	интеграле ∫dx	∫ f (x, y)dy
					0	− x

приводит его к виду:______________________________________.

118

15. Интеграл

∫∫

dxdy

π

, 0 ≤ r ≤ 2 sinϕ},

x

2

+ y

2 по области D ={(r,ϕ) : 0 ≤ ϕ ≤ 2

D

вычисленный

в

полярных

координатах,

равен

1. 1

2. 2

3. 0

4. − 2

5. -1.

16.

Расстановка

пределов

интегрирования

в

∫∫∫f (x, y, z)dxdydz

по

области

V ,

ограниченной

V

поверхностями:

y + x =1,

y = 0,

x = z,

x = 0,

z = 0 , приводит его к кратному интегралу

вида:______________________________________.

17.

Масса

тела

V ={(x, y, z) :

x > 0,

0 < y <1 − x, 0 < z < x}

с плот-

ностью

ρ(x, y, z) = 40xz

равна

1. 1

2.

2

3. 1,5

4. 0,5

5.2,5.

18.

Если

тело

V

ограничено

поверхностями

z 2 = x2 + y 2

x2 + y2 + z2 =1,

причем

z 2 ≤ x2 + y2 , то

его

объем,

вычисленный

в

сферических

координатах,

равен

1. 2 2π

2.

2π

3.

π

4.

π

5. π.

3

3

3

2

2

19.

∫3xdl ,

AB : x2 = 2y, A (0;0), B (

3;

3

Интеграл

где

2),

равен

AB

1. 7

2. 8

3. 9

4. 6

5. 5 .

20.

Интеграл

∫ydx − xdy ,

где

x = acos

t;

0

≤ t ≤ 2π,

равен

L :

L

y = bsin t,

1. 2πab

2. − 2πab

3. πab

4. − πab

5. 0.

119

4.

1.

Геометрический

смысл

интеграла

∫∫∫dV

есть _______________.

V

2.

По

свойству

аддитивности,

если

области

G , G1 и G2

такие,

что

G1 G , G2 = G \

а

функция

f (x, y) интегрируема

на G ,

то

G1,

f ____________

на

G1 и

G2 , причем ∫∫ fdG равен ___________.

G

3.

По

свойству

тройного

интеграла,

если

f (x, y, z)

и

f (x, y, z)

интегрируемы

на

V ,

то

для

∫∫∫f dV

и

∫∫∫

f

dV

выполняется

V

V

неравенство ________________________________.

4.

Если

формулы

x = x(u,v) ,

y = y(u,v)

задают

взаимно

однозначное

и непрерывно дифференцируемое

отображение

области

D плоскости

переменных (u,v) на

область

G

плоскости

переменных

(x, y) ,

то

∫∫ f (x, y) dx dy =∫∫

_________, где якобиан I (u,v) равен_____________.

G

D

5.

Статический

момент

M oy

относительно оси OY пластинки G с

плотностью

ρ(x, y)

((x, y) G)

равен_________________________.

6.

Абсцисса

x

центра

тяжести

тела

V R3 с плотностью

ρ(x, y, z) ,

(x, y, z) V равна_______________________________.

7.

Физический смысл криволинейного интеграла второго рода есть

_________.

8.

Если

f (x, y)

- непрерывная

функция на кусочно-гладкой

кривой

AB :

r = r(ϕ) (α ≤ ϕ ≤ β), то

∫ f (x, y)dl

вычисляется по формуле:_________.

AB

120

9.

Координаты

x

и

y центра масс

кусочно-гладкой

кривой

AB

с

плотностью

ρ(x, y)

(x, y) AB

вычисляются по формулам:_________.

10.

Если

P(x, y)

и

Q(x, y) - непрерывные

функции

в

односвязной

области

G

и

P(x, y)dx + Q(x, y)dy = dU (x, y)

(U (x, y)

- функция,

определенная

в

G ),

то

для

любых

точек

A

и

B

из

G

∫P(x, y)dx + Q(x, y)dy ________________________________.

AB

11.

Направляющие

косинусы нормали

cos (n ,k )

к

cos (n , i

) , cos (n , j),

ориентированной

поверхности

S :

z = f (x, y)

соответственно

равны _________________, __________________, _________________.

12.

Для

вектора

F

(x, y, z) = P(x, y, z) i

+ Q(x, y, z) j + R(x, y, z) k

дивергенцией

называется_____________________________________.

13. Двукратный интеграл для ∫∫ f (x, y)dxdy по области D , ограниченной

	D	y = x2 ,
кривыми:	y = −x ,			имеет
вид:__________________________.
			1	1−y2
14. Изменение порядка	интегрирования	в интеграле	∫dy	∫ f (x, y)dx
			0	1−y

приводит его к		виду:_______________________________.
15. Интеграл ∫∫	dxdy2		2	по области	D ={(r,ϕ) : 0 ≤ ϕ ≤ 2π,	0 ≤ r ≤ ϕ},
D	x	+ y
вычисленный			в	полярных	координатах,	равен
1. 2π2	2. 4π2			3. 8π2	4. ∞	5. 5.

121

16. Расстановка	пределов интегрирования в ∫∫∫f (x, y, z) dxdydz по области
		V
V , ограниченной поверхностями		y = x , y = x2 , z = x , z = 0 , x = 0 ,
приводит к	кратному интегралу	вида:_________________________.

17.

Масса

тела

V = {(x, y, z) : x > 0 , x2 < y < x,

0 < z < x

с

плотностью

ρ(x, y, z) = 40z

равна

1. 1

2. 2

3. 1,5

4. 0,5

5. 2,5.

18.

Если

тело

V

ограничено

поверхностями

z =1 − (x2 + y 2 ) ,

z = 0 ,

z ≥ 0 ,

то его объем, вычисленный

в цилиндрических

координатах,

равен

1. π

2.

π

3. π

4. 2π

5. 4π.

4

2

19.

Интеграл

∫3y dl ,

где

L :

x = a (t − sin t);

0 ≤ t ≤ 2π,

L

y = a (1 − cos t) ,

равен

2. 16a2

3. 32a2

4. 48a2

5. 24a2 .

1. 0

20. Интеграл

∫xydx + 3x2dy ,

где

AB :

y = x3 , A (0,0) ,

B (1,1),

AB

равен

1. 1

2.

2

3. 3

4.

4

5. 0.

122

5.

1.	Интеграл		∫∫dG		равен___________________________________.
			G
2.	По	свойству линейности,				если	функции f (x, y, z)		и	g(x, y, z) -
	интегрируемы			на V ,	тогда для		любых чисел	A	и	B интеграл
	∫∫∫(Af + Bg) dV равен__________________________________.
	V
3. По свойству			об оценке		тройного интеграла, если			f (x, y, z)		интегрируема
	на	V	и	m ≤ f ≤ M		( m, M − const ),		то		выполняется

неравенство____________________________________________.

4. Якобиан J (r,ϕ, z) отображения, определяемого цилиндрическими координатами r, ϕ, z , равен определителю___________________.

5. Абсцисса центра тяжести					x пластинки		G R2		с заданной плотностью
	ρ(x, y) ((x, y) G)			равна_________________________.
6.	Геометрический смысл тройного интеграла ∫∫∫dV									есть__________.
								V
7.	Если	f (x, y)	- непрерывная функция				на	кусочно-гладкой кривой			AB
	и	I1 = ∫ f (x, y) dl ,				I 2 = ∫ f (x, y) dl ,				то
		AB					BA
	1. I1 = −I2			2. I1 < I2			3. I1 > I2			4. I1 = I2 .
8.	Если	P(x, y)	и Q(x, y)		- непрерывные			функции		на кусочно-гладкой
	ориентированной			кривой		AB :	x = g(y),		c ≤ y ≤ d ,		то

123

∫P(x, y)dx + Q(x, y)dy вычисляется по формуле:_______________.

AB

9. Момент инерции Jox относительно оси OX кусочно-гладкой кривой AB

c плотностью ρ(x, y) вычисляется по формуле:_______________.

10.Если P(x, y) непрерывна вместе с ∂∂Py в замкнутой области G ,

ограниченной		кусочно-гладкой			кривой	L ,	то	∫∫	∂P	dxdy
									∂ y
равен___________________________________.								G
11. Если	функция		R(x, y, z)		непрерывна	на	кусочно-гладкой
ориентированной поверхности S :					z = f (x, y),	(x, y) D ( D -		замкнутая
ограниченная		область),		то	∫∫R (x, y, z) dxdy		вычисляется			по
					S

формуле:________________________________.

12. Формула Стокса в векторной форме имеет вид:_________________.

13.

Двукратный интеграл для

∫∫ f (x, y)dxdy

по области D , ограниченной

D

кривыми:

x + y = −1,

y = − 1− x2 ,

имеет

вид:______________.

1

x2

14.

Изменение

порядка

интегрирования в

интеграле

∫dx

∫ f (x, y)dy

0

− x

приводит

его

к

виду:________________________________.

15.

Интеграл

∫∫x dxdy

по

области

D = {(x, y) : x2 + y 2 ≤1, x ≥ 0, y ≥ 0},

D

вычисленный

в

полярных

координатах,

равен

1. 0,5

2. 0

3. −

1

4.

1

5. –0,5.

3

3

124

16.

Расстановка

пределов

интегрирования

в

∫∫∫f (x, y, z) dxdydz

по

V

области

V ,

ограниченной поверхностями: y + x =1, x2 =1− y ,

z = x2 ,

z = 0 , x = 0 , приводит к кратному интегралу вида:________.

17.

Масса тела

V ={(x, y, z) : x > 0; 1 − x < y <1 − x2 ; 0 < z < x2 }

с

плотностью

ρ(x, y, z) = 42z

равна

1. 1

2.

2

3. 0,25

4. 0,5

5. 1,25.

18.

Если

тело

V

ограничено

поверхностями

x2 + y2 = 4 ,

x2 + y2 + z2 = 4, z = 2 ,

причем

z ≥ 0 , то

его

объем,

вычисленный

в

цилиндрических

координатах,

равен

1. π

2.

4π

3. 4π

4.

8π

5. 3π.

3

3

19.

Интеграл

∫

dl

,

где AB : x2 = 2y ,

A(0,0),

B(2,2) , равен

AB

1 + x2

1. 1

2. 2

3. 3

4. − 2

5. −1.

20.

Интеграл

∫ydx + xdy ,

где

L :

x = R cos t ;

0 ≤ t ≤

π

равен

4

L

y = R sin t ,

1. R2

2.

R2

3. 2R 2

4. −

R2

5. − R 2 .

2

2

125

6.

1.

Тройным

интегралом

от

функции f (x, y, z) ,

непрерывной в

замкнутой

области

,

называется __________________________.

V

2.

По

свойству

монотонности

тройного

интеграла, если функция

f (x, y, z)

неотрицательна и

интегрируема

на

G ,

то

выполняется

неравенство _______________________________.

3.

По

свойству

линейности,

если

функции

f (x, y, z)

и

g(x, y, z)

интегрируемы

на

V ,

тогда

для

любых

чисел A

и

B сумма

A∫∫∫fdV + B∫∫∫gdV

равна __________________________________.

VV

4.Если формулы x = x(u,v,w) , y = y(u,v,w) , z = z(u,v,w) задают взаимно

однозначное и непрерывно дифференцируемое отображение области T пространства переменных (u,v,w) на область Ω пространства

	переменных		(x, y, z) , то ∫∫∫dxdydz = ∫∫∫ ___________________, где
	якобиан	I (u,v,w)		Ω		T
				равен _______________________________.
5.	Моменты	инерции		I x , I y	пластинки		G R2 с	плотностью
	ρ(x, y) ,	((x, y) G)		равны __________________________________.
6.	Если область			V ={(x, y, z) :		(x, y) G, ϕ(x, y) ≤ z ≤ ψ(x, y)},			где
	функции	ϕ и	ψ интегрируемы		в	G , то	∫∫∫dV равен	двойному
							V

интегралу вида: ______________________________________.

7.	Если	P(x, y)	и	Q(x, y) - непрерывные функции на ориентированной
	кусочно-гладкой			кривой	AB и	I1 = ∫P(x, y) dx + Q(x, y) dy ,
	I 2 = ∫P(x, y) dx + Q(x, y) dy ,					AB
					то
		BA
	1. I1 = −I 2			2. I1 < I 2	3. I1 > I 2		4. I1 = I2 .
8.	Если	f (x, y)	-	непрерывная	функция	на кусочно-гладкой кривой

126

AB : x = ϕ(t) ;

t2 <t <t1,

то

∫ f (x, y) dl

вычисляется

по

y = ψ(t) ,

AB

формуле: ________________________________.

9.

Если

f (x, y)

и

f (x, y)

интегрируемы на кусочно-гладкой

кривой

AB

и

I1 =

∫ f (x, y) dl

I 2 = ∫

f (x, y)

dl ,

то

,

AB

AB

1. I1 ≤ I 2

2. I1 = I 2

3. I1 ≥ I 2

4. I1 > I2 .

10.

Если функции P(x, y)

и

Q(x, y) непрерывны вместе с

∂ P

и

∂Q

∂ x

∂ y

в односвязной области

G

и

∂ P

=

∂Q

,

то для любых точек

A

и

∂ y

∂ x

B из

G

∫P(x, y)dx + Q(x, y)dy ____________________________.

AB

11.

Масса

кусочно-гладкой

поверхности

S

с

плотностью

ρ(x, y, z) ,

(x, y, z) S

равна __________________________.

12.

Если

функции

P(x, y, z) , Q(x, y, z) и

R(x, y, z)

непрерывны

на

кусочно-гладкой

ориентированной

поверхности

S ,

то

∫∫P(x, y, z)dydz + Q(x, y, z)dzdx + R(x, y, z)dxdy

через

поверхностный

S

интеграл первого рода представляется в виде: __________________.

13. Двукратный интеграл для ∫∫ f (x, y)dxdy по области D , ограничен-

D

ной кривыми: x − y = 2 , y = − 4 − x2 , имеет вид: _______________.

127

0 −y

14. Изменение порядка интегрирования в интеграле ∫dy ∫ f (x, y) dx

−1 3 y

приводит его к виду: _____________________________.

15.

Интеграл

∫∫

ydxdy

по

области

D ={(x, y) : x2 + y 2 ≤ 4, y ≥ 0},

x

2 2

D

+ y

вычисленный

в

полярных координатах,

равен

1. 1

2. 2

3. −2

4. 4

5. 0.

16. Расстановка

пределов интегрирования в ∫∫∫f (x, y, z) dxdydz по области

V

V , ограниченной поверхностями:

z = x ,

y =x,

y =

x ,

z = 0 , x = 0 ,

приводит его к кратному

интегралу

вида: _______________.

17.

Масса

тела

V = {(x, y, z) :x > 0;x < y <

x;0 < z < x}

с

плотностью

ρ(x, y, z) =14x

равна

1. 1

2. 0,5

3. 1,5

4. 0,25

5. 0,75.

18.

Если

тело

V

ограничено

поверхностями

z 2 = x2 + y2 ,

z = x2 + y2 ,

причем

0 ≤ z ≤1,

то

его

объем,

вычисленный в

цилиндрических

координатах,

равен

1. π 6

2. π 3

3. π 2

4. π

5. π 4 .

19. ∫ 2 z(x2 + y 2 )dl ,		где
L
1. 4a4π2	2. 2a3π2

x = a cos t ;
	= a sin t ;	0 ≤ t ≤ 2π,	равен
L : y
	= a t ,
z
3. 4a2π2		4. 2a4π2	5. 4a3π2 .

20. ∫4xydx + 6( y − x) dy ,		где AB : y = x2 ,	A(0,0), B(1,1),	равен
AB
1. 1	2. 2	3. 0	4. −2	5. −1.

128

7.

1.

Если функция

ρ(x, y, z) , (x, y, z) V ,

- плотность распределения масс,

то физический смысл интеграла

∫∫∫ρ(x, y, z)dxdydz

есть __________.

V

2.

По свойству аддитивности,

если области G , G1 и G2 такие, что G1 G ,

G2 = G \

и

функция

f (x, y)

-

интегрируема

в

G ,

то

G1

f (x, y) ________________________

на

G1

и G2 ,

причем сумма

∫∫ f dG

+ ∫∫ f dG

равна ___________________________________.

G1

G2

3.

По свойству

монотонности для

тройного

интеграла,

если

функция

f (x, y, z) -

неотрицательна и интегрируема на V R3 ,

то выполняется

неравенство __________________________________.

4.

Если

формулы

x = x(u,v) ,

y = y(u,v)

задают

взаимно

однозначное и непрерывно дифференцируемое отображение области

D

плоскости переменных (u,v)

на область G плоскости переменных (x, y) ,

то якобиан

I (u,v)

отображения равен ___________________________.

5.

Момент

инерции I 0 относительно начала координат

пластинки

G R2

с плотностью

ρ(x, y) ,

(x, y) G ,

равен __________________________.

6.

Ордината

центра

тяжести

y

тела

V R3

с

плотностью

ρ(x, y, z) ,

(x, y, z) V ,

равна _______________________________.

7.

Интеграл вида

∫P(x, y)dx + Q(x, y)dy

называется ________________.

AB

129

8. Если	f (x, y, z)	- непрерывная	функция на кусочно-гладкой кривой
	x = ϕ(t);
AB :		t1 ≤ t ≤ t2 ,	то	∫ f (x, y, z)dl	вычисляется по
	y = ψ(t);
				AB
	z = χ(t) ,

формуле: _________________________________.

9.

Масса кусочно-гладкой кривой

AB

по

заданной

плотности ρ(x, y) ,

(x, y) AB

вычисляется

по

формуле: ___________________________.

10.

Если

функции

P(x, y) и

Q(x, y) - непрерывны

в

односвязной

области

с кусочно-гладкой ориентированной границей Г и для

G

любых точек

A

и B

из

G

∫P(x, y)dx + Q(x, y)dy

не зависит от

AB

пути

интегрирования,

а

I = ∫P(x, y)dx + Q(x, y)dy ,

то

Г

1. I < 0

2. I = 0

3. I > 0

4. I ≠ 0 .

11.

По теореме о сведении поверхностного интеграла первого рода к

двойному,

если

функция

f (x, y, z)

непрерывна

на

кусочно-гладкой

поверхности

S :

z = z(x, y)

((x, y) D ,

D

- замкнутая

ограниченная

область плоскости XOY ),

то

∫∫ f (x, y, z)dS = ∫∫

________________.

S

D

12.

Ротором

(вихрем)

вектора

(x, y, z) = P(x, y, z)

+

F

i

+ Q(x, y, z)

+ R(x, y, z)k

называется __________________________.

j

13.

Двукратный

интеграл

для

∫∫ f (x, y)dxdy

по области

D ,

ограничен-

y = −x3,

D

ной

кривыми:

y = −x , имеет

вид: ____________________.

130

1

2−y

14.

Изменение

порядка

интегрирования

в

интеграле

∫dy

∫ f (x, y)dx

0

y

приводит его

к

виду: ______________________________.

15.

Интеграл

∫∫

xdxdy

по

области

D ={(x, y) : x2 + y 2 ≤1,

x

2

+ y

2

D

x ≥ 0, y ≥ 0},

вычисленный

в

полярных

координатах,

равен

1. 1

2. −1

3. 0,5

4. ∞

5. − 0,5 .

16.

Расстановка

пределов

интегрирования

в

∫∫∫f (x, y,z)dxdydz по области

z = x ,

V

V , ограниченной поверхностями:

y − x =1,

x = 0 ,

y = 0 ,

z = 0,

приводит его к кратному интегралу вида: ________________________.

17.

Масса

тела

V ={(x, y, z) : x < 0; 0 < y < x +1; x < z < 0} с

плотностью

ρ(x, y, z) = −24x

равна

1. 1

2. 2

3. 0,5

4. 1,5

5. 2,5.

18.

Если

тело

V

ограничено

поверхностями

z = x2 + y2 ,

z = 0,

z 2 + y2 = 4,

причем

z ≥ 0,

то

его

объем, вычисленный в

цилиндрических

координатах,

равен

1. 2π

2. 8π

3. 16π

4. 4π

5. 12π.

19.

∫ 2aydl ,

где

x

= a (t − sin t);

0 ≤ t ≤ 2π,

равен

L :

L

y = a (1 − cos t),

1. 4aπ

2. 4a2π

3. 8a2π

4. 2a2π

5. 2aπ.

20. Интеграл	∫x dy − y dx ,	где L :	x2 + y 2 = 4 (обход	контура L -
	L
против часовой стрелки),		равен
1. 4π	2. 8π	3. 2π	4. −8π	5. − 4π.

131

8.

1.

Масса

пластинки

G R 2

с плотностью ρ(x, y) ,

(x, y) G

равна ______________________________.

2.

По

свойству

об

оценке

двойного

интеграла,

если

f (x, y)

интегрируема

на G

и

m ≤ f ≤ M

( m,M − const ),

то выполняется

неравенство _______________________________.

3.

По

свойству

аддитивности,

если области

V , V1

и V2

такие,

что

V1 V ,

V2 =V \

и

функция

f (x, y, z)

-

интегрируема

на

V ,

то

V1

f __________________________

на

V1

и

V2 ,

причем

сумма

∫∫∫f dV + ∫∫∫f dV

равна __________________________________.

V1

V2

4.

Если отображение

области

T

пространства переменных

(r,ϕ, z) на

область

Ω

пространства

переменных

(x, y, z) определяется

цилин-

дрическими координатами,

то

∫∫∫f (x, y, z)dxdydz =∫∫∫ ___________.

Ω

T

5. Согласно геометрическому смыслу двойного интеграла объем замкнутой области V ={(x, y,z) : (x, y) G, ϕ(x, y) ≤ z ≤ ψ(x, y)}, где функции ϕ и ψ интегрируемы в G , равен ____________________.

6.

Момент

инерции

I z относительно оси

Oz тела

V R3 с

плотностью

ρ(x, y, z) , (x, y, z) V ,

равен _____________________.

7.

Работа

вектора

силы

(x, y) = P(x, y)

+ Q(x, y)

при

F

i

j

перемещении

вдоль

кусочно-гладкой

кривой

AB (

(x, y)

непрерывна

F

на AB ) вычисляется по формуле: ______________________________.

132

8.

Если

Q(x, y, z)

-

непрерывная

функция

на

кусочно-гладкой

x = ϕ(t);

= ψ(t);

t1 ≤t ≤t2,

то

∫Q(x, y, z)dy

ориентированной кривой AB : y

= χ(t) ,

AB

z

вычисляется по формуле: _______________________.

9.

Статический

момент

M X

относительно

оси

OX

кусочно-гладкой

кривой AB с плотностью ρ(x, y) , (x, y) AB вычисляется по формуле:

___________________________.

10.

Если

Q(x, y)

непрерывна

вместе

с

∂Q

в замкнутой

области G ,

∂ x

ограниченной

кусочно-гладкой

кривой

L ,

то

∫∫

∂Q

dxdy

∂ x

равен __________________________.

G

11.

По

определению,

если

вектор-функция

(x, y, z) =

F

непрерывна на

кусочно-гладкой

= P(x, y, z)i

+ Q(x, y, z) j + R(x, y, z)k

ориентированной

поверхности S ,

то поверхностный интеграл второго

рода в векторной форме имеет вид: ___________________________.

12. По формуле Остроградского – Гаусса интеграл от дивергенции вектор-

функции F(x, y, z) = P(x, y, z)i + Q(x, y, z) j + R(x, y, z)k , непрерывной в замкнутой области V , ограниченной замкнутой ориентированной поверхностью S , равен _________________, где _________________.

13. Двукратный интеграл для ∫∫ f (x, y)dxdy по области D , ограничен-

D

ной кривыми: y = x2 , x = −y2 , имеет вид : _______________________.

133

1

x

14.

Изменение порядка интегрирования в

интеграле

∫dx ∫ f (x, y) dy

приводит

его

к

виду: ________________________.

0

−x

15. Интеграл

∫∫

dxdy2

2

по области D ={(r,ϕ) :− π2 ≤ ϕ≤ π2 ,

0 ≤ r ≤ cos ϕ},

D

x

+ y

вычисленный

в

полярных координатах,

равен

1. 1

2. 2

3. 0

4. ∞

5. −2 .

16.

Расстановка

пределов

интегрирования

в

∫∫∫f (x, y, z) dxdydz

по

V

области

V ,

ограниченной поверхностями:

z = x , z = −x ,

y + x +1 = 0 ,

y − x −1 = 0,

x = 0 ,

приводит

его

к

кратному

интегралу

вида: _______________________________.

17.

Масса

тела

V ={(x, y, z) : x < 0, − x −1< y < x +1,

x < z < −x}

с

плотностью

ρ(x, y, z) = x2

равна

1. 1

2. 0,2

3. 0,5

4. 0,25

5. 0,75.

18. Если тело			V	ограничено поверхностями x2 + y2 + z2 =1,					z2 = x2 + y2 ,
причем z 2 ≥ x2 + y 2 и z ≤ 0 , то его объем, вычисленный								в сферических
координатах,				равен
1.	2π			2.	2π	3.	2 − 2 π	4. π	(1 −	1 ) .
					3
3							3	3		2
19. Интеграл			∫	6x dl	,	где AB :	y 2 = 2x , A (0,0) ,	B (2,2) ,		равен
			AB	1 + y 2
1. −8				2. 2		3. 8	4. 4		5. − 4.

134

20. Интеграл	∫(x +1)dy − ( y + 2)dx , где		L : x = R cos t;	0 ≤ t ≤ 2π, равен
	L		y = R sin t,
1. πR 2	2. 2πR 2	3. 0	4. − 2πR 2	5. − πR 2 .

9.

1. Площадь области G XOY равна ___________________________.

2.

По

свойству

двойного

интеграла, если

∫∫

f (x, y)

и

f (x, y)

интегрируемы

на

G ,

то

для

∫∫ f dG

и

f

dG

выполняется

G

G

неравенство _____________________________.

3.

Если

функции

f (x, y,z)

и

g(x, y, z)

интегрируемы

на

V ,

f (x, y, z) ≤ g(x, y, z) на V

и

A = ∫∫∫f (x, y, z) dV ,

B = ∫∫∫g(x, y, z) dV ,

то

V

V

1. A > B

2. A ≤ B

3. A ≥ B

4. A < B

5. A = B .

4.

Если

функции

x = x(u,v,w) ,

y = y(u,v,w) ,

z = z(u,v,w)

задают

взаимно однозначное и непрерывно дифференцируемое отображение

области

Ф

пространства переменных

(u,v,w) на

область

Ω

пространства

переменных

(x, y, z) ,

и

якобиан

отображения

I (u,v,w) равен __________,

то

∫∫∫f (x, y, z) dxdydz = ∫∫∫

__________.

Ω

Τ

5.

Если

ρ(x, y) ,

((x, y) G) -

плотность

распределения

масс, то

механический смысл

интеграла

∫∫y 2ρ(x, y)dxdy

есть _____________.

G

6.

Аппликата

центра

тяжести

z

тела

V R3

с плотностью

ρ( x, y,z ),

(x, y, z) R3

равна _________________________________.

135

7. Если P(x, y) - непрерывная функция на кусочно-гладкой ориенти-

рованной	кривой	AB	и	I1 = ∫ P(x, y)dx , I 2 = ∫P(x, y)dx ,						то
1. I1 = I2		2. I1	> I2		AB	3. I1 < I2		BA	4. I1 = −I2 .
8. Если P(x, y) и		Q(x, y)		непрерывные		функции		на кусочно-гладкой
ориентированной		кривой		AB ,	то		∫P(x, y)dx + Q(x, y)dy			через
							AB
криволинейный		интеграл			первого		рода	представляется в
виде: ____________________________.
9. Если неотрицательная			функция		f (x, y)		интегрируема		на кусочно-
гладкой	кривой	AB ,		то для		I = ∫ f (x, y) dl			справедливо
							AB
1. I ≤ 0	2. I = 0			3. I ≥ 0			4. I ≠ 0		5. I > 0.

	10. Если P(x, y) и Q(x, y)		непрерывны	вместе	с	∂ P	и	∂ Q
						∂ y		∂ x
	односвязной области G	и	для любых точек А и В из
	∫P(x, y)dx + Q(x, y)dy	не	зависит от	пути	интегрирования,

AB

в

G

то

1.

∂ P

=

∂ Q

2.

∂ P

<

∂Q

3.

∂ P

=

∂Q

4.

∂ P

>

∂Q

.

∂ y

∂ x

∂ y

∂ y

∂ x

∂ x

∂ x

∂ y

11.

Если

функция

P(x, y, z)

непрерывна

на

кусочно-гладкой

ориентированной

поверхности

S: x = h (y, z),

(( y, z) D,

D −

замкнутая

ограниченная

область

плоскости

YOZ ),

то

∫∫P(x, y, z) dydz

равен ______________________________________.

S

12.

По

формуле

Стокса

поток

вектора

rot

(

(x, y, z) =

F

F

через

поверхность

S

с краем Г,

= P(x, y, z)i

+ Q(x, y, z) j + R(x, y, z)k )

являющимся кусочно–гладкой ориентированной замкнутой кривой,

равен __________________________, где _________________________.

136

13.

Двукратный интеграл для

∫∫ f (x, y)dxdy

по области D ,

ограничен-

D

ной кривыми:

y = x2 , y =

2 − x2 ,

имеет

вид: __________________.

0

−y

14.

Изменение порядка интегрирования

в

интеграле

∫dy ∫ f (x, y)dx

−1

−y

приводит

его к

виду: _________________________.

15.

Интеграл

∫∫

dxdy2

2

по

области

D ={(x, y) : x2 + y 2 ≤1,

y ≥ 0},

D

x + y

вычисленный

в

полярных

координатах,

равен

1. 0

2. 2π

3. π

4. π

2

5. − 2π.

16.

Расстановка пределов

интегрирования

в

∫∫∫f (x, y,z) dxdydz

по

V ,

V

области

ограниченной

поверхностями:

z = y,

x = y 2 −1,

y − x −1 = 0, y = 0 ,

приводит

к

кратному

интегралу

вида: _______________________________.

17.

Масса

тела

V ={(x, y, z) : y > 0, y 2 −1 < x < y −1, 0 < z < y}

с

плотностью

ρ(x, y, z) = 40y

равна

1. 1

2.

2

3. 9

4. 18

5. 6.

18.

Если тело V ограничено поверхностями

x2 + y2 + z2 = 4,

z =1, причём

z ≥1,

то

его

объём,

вычисленный

в

цилиндрических

координатах,

равен

5π

5π

1.

5π

2.

5π

3.

4.

5. 5π.

4

3

2

6

x = t;

19.

Интеграл

∫6x dl ,

где

L :

= t 2

2 ;

0 ≤ t ≤1,

равен

y

L

= t 3

3,

z

4,5

1. 1

2. 2

3. 3

4.

5. 5 .

137

20. ∫(5x2 + 3y 2 )dy ,

где

AB : y = x3 , A (0,0), B (1,1),

равен

AB

1. 1

2.

2

3. 3

4.

4

5.

5.

138

Учебное издание

ЧЕБАНОВА Наталья Анатольевна ГИЛЬМУТДИНОВА Альфия Ямгутдиновна ЧЕБАНОВ Владимир Иванович

СБОРНИК ТЕСТОВЫХ ЗАДАНИЙ ПО МАТЕМАТИКЕ ДЛЯ ВУЗОВ

ЧАСТЬ 2

2-е издание

Редактор Медведева Г.Р.

ЛР № 020258 от 08.01.98

Подписано к печати 26.12.01 . Формат 60x84 1/16. Печать плоская. Бумага писчая. Гарнитура Times New Roman.

Усл. печ. л.	9,0	Усл. кр.-отт. 8,9		Уч.-изд. л. 8,9
Тираж 250	экз.	Заказ №	С ( 48 )

Уфимский государственный авиационный технический университет Уфимская типография №2 Министерства печати и массовой информации Республики Башкортостан 450000, Уфа-центр, ул. Карла Маркса, 12

139