Глава IV

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

§ 1. Дифференциальные уравнения первого порядка

1. Основные понятия. Дифференциальным уравнением называется уравне­ние, связывающее независимые переменные, их функцию и производные (или дифференциалы) этой функции. Если независимая переменная одна, то урав­нение называется обыкновенным; если же независимых переменных две или больше, то уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Например:

1) —обыкновенное дифференциальное уравнение первого по­ рядка;

2) —обыкновенное дифференциальное уравнение второго

порядка;

3. —обыкновенное дифференциальное уравнение третьего порядка;

4. F (х, у, у',y") = 0 —общий вид обыкновенного дифференциального урав­нения второго порядка;

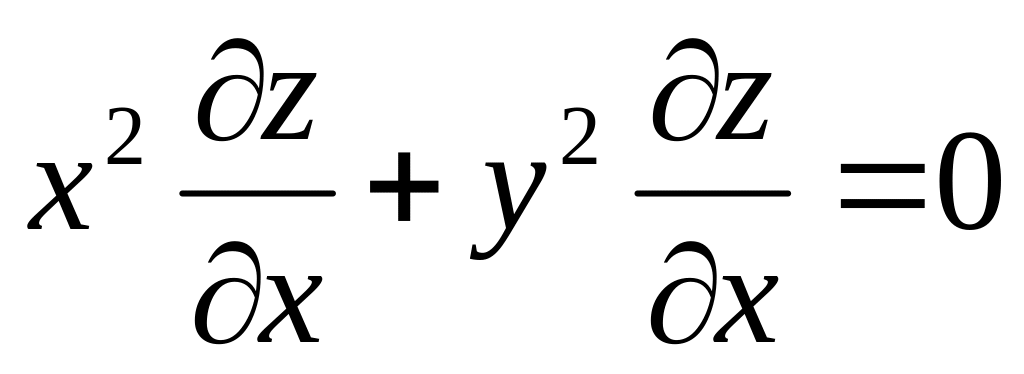5. —уравнение в частных производных первого порядка.

В этом параграфе рассматриваются обыкновенные дифференциальные уравнения первого порядка, т. е. уравнения вида F (х, у, у')=0 или (в раз­решенном относительно у' виде) у'=f(х, у).

Решением дифференциального уравнения называется такая дифференци­руемая функция у' = φ(х), которая при подстановке в уравнение вместо неиз­вестной функции обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциаль­ного уравнения.

Общим решением дифференциального уравнения первого порядка у' == f(х,y) в области D называется функция у = φ(х,С), обладающая сле­дующими свойствами: 1) она является решением данного уравнения при лю­бых значениях произвольной постоянной С, принадлежащих некоторому мно­жеству; 2) для любого начального условия у(х₀) = у₀ такого, что (х₀, у₀)€D, существует единственное значение С = С₀, при котором решение у = φ (х, С₀) удовлетворяет заданному начальному условию.

Всякое решение у = φ (х, С₀), получающееся из общего решения y= φ (х. С) при конкретном значении С = С₀, называется частным решением.

Задача, в которой требуется найти частное решение уравнения у'=f(х, у), удовлетворяющее начальному условию у(х₀)=y₀, называется задачей Коши.

Построенный на плоскости хОу график всякого решения y = φ (x) диффе­ренциального уравнения называется интегральной кривой этого уравнения. Таким образом, общему решению у = φ (х, С) на плоскости хОу соответствует семейство интегральных кривых, зависящее от одного параметра —произволь­ной постоянной С, а частному решению, удовлетворяющему начальному усло­вию у(х₀)=у₀,—кривая этого семейства, проходящая через заданную точку M₀ (х₀; y₀).

Если функция f(х, у) непрерывна и имеет непрерывную производную в области D, то решение дифференциального уравнения у'=f (х, у) при началь­ном условии у(х₀)=y₀ , существует и единственно, т. е. через точку (x₀; у₀) проходит единственная интегральная кривая данного уравнения (теорема Кош и).

Особым решением называется такое решение, во всех точках которого условие единственности не выполняется, т. е. в любой окрестности каждой точки (х; у) особого решения существуют по крайней мере две интегральные кривые, проходящие через эту точку.

Особые решения не получаются из общего решения дифференциального управления ни при каких значениях произвольной постоянной С (в том числе и при С= ± ∞).

Особым решением является огибающая семейства интегральных кривых (если она существует), т. е. линия, которая в каждой своей точке касается по меньшей мере одной интегральной кривой.

Например, общее решение уравнения записывается в виде у = sin(х+С). Это семейство интегральных кривых имеет две огибающие: у=1 и у = —1, которые и будут особыми решениями.

2. Дифференциальные уравнения с разделяющимися переменными. Диффе­ренциальное уравнение вида

относится к типу уравнений с разделяющимися переменными. Если ни одна из функций f₁ (х), f₂ (х), φ₁ (у), φ ₂ (y) не равна тождественно нулю, то в ре­зультате деления исходного уравнения на f₂ (x) φ₁ (у) оно приводится к виду

Почленное интегрирование последнего уравнения приводит к соотношению

которое и определяет (в неявной форме) решение исходного уравнения. (Реше­ние дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения.)

507. Решить уравнение . Решение. Разделив обе части уравнениия на , имеем

Интегрируя, находим

или

Это общее решение данного дифференциального уравнения.

Пусть теперь у²—4 = 0, т. е. у=±2. Непосредственной подстановкой убеждаемся, что у=±2 — решение исходного уравнения. Но оно не будет осо­бым решением, так как его можно получить из общего решения при С = 0.

508. Найти частный интеграл уравнения у'соsх = у/lпу, удовлетворяющий начальному условию y(0)=1.

Решение. Полагая . перепишем данное уравнение в виде

Разделяем переменные:

Проинтегрируем обе части уравнения:

или

Используя начальное условие у=1 при х = 0, находим С = 0. Окончательно получаем

509. Найти общий интеграл уравнения у' = tgх tg у.

Решение. Полагая у' =dy/dx и разделяя переменные, приходим к уравнению сtg y dy=tg x dx. Интегрируя, имеем

, или ln|siny|=-ln|cosx|+lnC.

Отсюда находим sin y = С/соsx, или siпусоsх = С (общий интеграл).

510. Найти частное решение дифференциального уравнения (1+x²)dy+уdx= 0 при начальном условии y(1)=1.

Решение. Преобразуем данное уравнение к виду . Интегрируя,

получим

, или ln|y|=-arctgx+C.

Это и есть общий интеграл данного уравнения.

Теперь, используя начальное условие, найдем произвольную постоянную С; имеем ln1= — arctg 1+С, т. е. С = π/4. Следовательно,

lny = — агсtgx+ π /4,

откуда получаем искомое частное решение у = е^{π/4-агсtgх}.

________________

Решим несколько геометрических и физических задач, приводящих к диф­ференциальным уравнениям рассматриваемого типа.

512. Цилиндрический резервуар с высотой б м и диаметром основания 4 м поставлен вертикально и наполнен водой. За ка­кое время вода, заполняющая резервуар, вытечет из него через круглое отверстие радиуса 1/12 м, сделанного в дне резервуара?

Решение:

Для решения поставленной задачи надо воспользоваться формулой Бернулли, определяющей скорость v (в м/с) истечения жидкости из отверстия в резервуаре, находящегося на h м ниже свободного уровня жидкости:

Здесь g = 9.8 м/с² — ускорение силы тяжести, σ — постоянный (безразмер­ный) коэффициент, зависящий от свойств жидкости (для воды σ ≈ 0.6).

Пусть через t с после начала истечения воды уровень оставшейся в ре­зервуаре воды был равен h м, и за время dt c понизился еще на dh м (dh<0). Подсчитаем объем воды, вытекшей за этот бесконечно малый промежуток вре­мени dt, двумя способами.

С одной стороны, этот объем dω равен объему цилиндрического слоя с высотой |dh| и радиусом, равным радиусу r основания резервуара (r =2 м). Таким образом, dω = πr² |dh| = - πr² dh

С другой стороны, этот объем равен объему цилиндра, основанием кото­рого служит отверстие в дне резервуара, а высота равна Vdt (где v—скорость истечения). Если радиус отверстия равен р

(р = 1/12 м), то dω = πр²Vdt = .

Приравнивая эти два выражения для одного и того же объема, приходим к уравнению

Разделяя переменные и интегрируя, получаем

При t = 0 имеем h = h₀ = 6 м. Отсюда находим

Таким образом, связь между t и h определяется уравнением

в полное время истечения Т найдем, полагая в этой формуле h=0:

Используя данные задачи (r = 2 м, h₀=6 м, σ = 0.6, р=1/12 м, g= 9,8 м/с²), находим

Т ≈1062 с ≈ 17,7 мин.

513. В комнате, где температура 20° С, некоторое тело осты­ло за 20 мин от 100 до 60° С. Найти закон охлаждения тела; через сколько минут оно остынет до 30° С? Повышением темпе­ратуры в комнате пренебречь.

Решение:

В силу закона Ньютона (скорость охлаждения пропорциональна раз­ности температур) можем записать:

или т.е.

Если t=0, то T=100°; отсюда С = 80. Если t =20, то Т = 60°; значит, ln(40) = 20k+ln(80), откуда k = - (1/20)ln(2). Итак, закон охлаждения тела имеет вид

или

При T=30° имеем 10 = 80(1/2)^t/20, или (1/2)^t/20 = 1/8. Таким образом, t/20 = 3, откуда t = 60 мин.

514. Определить время, необходимое для установления оди­накового уровня жидкости в двух сообщающихся сосудах. Малое отверстие между сосудами имеет площадь ω м². Площади горизонтальных сечений первого и второго сосудов составляют S₁ м² и S₂ м², в начальный момент уровень жидкости в первом сосуде находился на высоте h₁ м от отверстия, а во втором — на высо­те h₂ м (h₂ < h₁).

Решение:

Пусть через t с после начала истечения жидкости уровень воды в пер­вом сосуде понизился до z₁ м, а во втором повысился до z₂ м. За дальнейший бесконечно малый промежуток времени dt с в первом сосуде уровень жидкости понизился на dz₁ м (dz₁ < 0), а во втором повысился на dz₂ м (dz₂>0).

Так как уменьшение объема жидкости в первом сосуде равно его увели­чению во втором, то

S₁|dz₁|=S₂|dz₂| или –S₁dz₁=S₂dz₂, откуда dz₂= -(S₁/ S₂)dz₁.

Если ввести обозначение u = z₁ - z₂, то скорость протекания жидкости через отверстие между сосудами можно найти по формуле ; она определяется формулой Бернулли (см. задачу 512), в которой следует поло­жить, что отверстие находится на глубине u = z₁ - z₂ под свободным уровнем жидкости.

Поэтому объем жидкости, протекающий за время dt, равный согласно предыдущему –S₁dz₁, в то же время равен . Приравнивая эти выражения для одного и того же объема, приходим к уравнению

Но dи = dz₁ - dz₂=dz₁+(S₁/S₂)dz₁, т. е. dz₁ =S₂du /(S₂ + S₁). Подставляя полученное для dz_1, выражение в предыдущее уравнение, находим дифферен­циальное уравнение, связывающее и и t:

или

Интегрируя, находим

При t=0 имеем u=h₁—h₂, откуда . Искомое время Т, необходимое для выравнивания уровней в сосудах, найдем, полагая u=0.

Решить уравнения:

515. lп соsу dх+х tg уdу=0.

516. .

517.

518. .

519. .

520. .

521. .

522. .

523. у/у'=lпу; у(2)=1

524.

525.

526. y’+sin(x+y)=sin(x-y)

527. уу' = — 2хsес у.

528. y(0)=0

529. y’=sh(x+y)+sh(x-y)

530.

531. ; y(1)=1

532. ; y(0)=1

533.

534. ; y(π/4)=0

535.

536.

537. ; y(π/4)= π/4

538.

539. Найти кривую, у которой отрезок касательной, заклю­ченный между осями координат, делится пополам в точке каса­ния.

540. Скорость обесценивания оборудования вследствие его износа пропорциональна в каждый данный момент времени его фактической стоимости. Начальная стоимость равна Лд. Найти стоимость оборудования по истечении I лет.

541. Некоторое вещество преобразуется в другое со ско­ростью, пропорциональной количеству непреобразованного ве­щества. Известно, что количество первого равно 31,4 г по исте­чении 1 ч и 9,7 г по истечении 3 ч. Определить: 1) сколько ве­щества было в начале процесса; 2) через сколько времени после начала останется 1% первоначального количества.

542. Цилиндрический резервуар длиной 6 м и диаметром 4 м расположен горизонтально. За какое время вода вытечет из ре­зервуара, если отверстие радиуса 1/12 м находится на уровне самой нижней из образующих цилиндра?

543. В коническую воронку с отверстием площадью (о см² и углом 2а при вершине конуса налита вода до уровня Н см над отверстием. Найти зависимость между переменной высотой уров­ня воды h в воронке и временем истечения t. Определить пол­ное время истечения. Вычислить его при ω=0,1 см², α=45°, Н =20 см.

544. Найти время, в течение которого вся вода вытечет из конической воронки, если известно, что половина воды вытекает за 2 мин.

3. Однородные дифференциальные уравнения. Уравнение вида Р(х,у)dх+Q(x,y)dy=0 называется однородным, если Р (х, у) и Q(х, у)—однород­ные функции одного измерения. Функция f (х, у) называется однородной изме­рения т, если

Однородное уравнение может быть приведено к виду у'=f(y/x). С помощью подстановки у=tх однородное уравнение приводится к уравнению с разде­ляющимися переменными по отношению к новой неизвестной функции t.

545. Найти общий интеграл уравнения

(х²+2ху)dх+хуdу=0.

Решение: Здесь Р (х, у) = х² + 2хy, Q(х, у) =ху. Обе функции—однородные вто­рого измерения. Введем подстановку у=tх, откуда dу == хdt+tdx. Тогда уравнение примет вид

(х² +2 х² t)dx+t х² (xdt+tdx)= 0, или (х² + 2 х² t + 2 х² t²) dx+t х³ dt = 0.

Разделяя переменные и интегрируя, имеем

;

Преобразуем второй интеграл:

или

Возвращаясь к прежней неизвестной функции у (t=у/х), получаем оконча­тельный ответ:

546. Найти частное решение уравнения - при начальном условии y(1)=π/2.

Решение: Произведем подстановку у/х=t, откуда у=tх, dу=хdt+tdx. В ре­зультате получаем

хdt+tdx=(t+sint)dx; xdt=sintdx;

Интегрируя, имеем

Ln|tg(t/2)|=ln|x|+lnC, откуда t/2 = агсtg (Сx).

Производя обратную замену t=y/х, находим общее решение исходного урав­нения у=2xarctg(Сх). Используя заданное начальное условие, получим π/2=2аrсtgС, откуда С=1. Итак, искомое частное решение имеет вид у=2arctgx

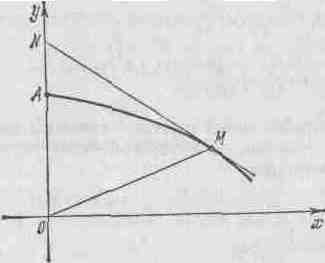
547. Найти кривую, проходящую через точку А (0; 1), для которой треугольник, образованный осью Оу, касательной к кри­вой в произвольной ее точке и радиусом-вектором точки касания,— равнобедренный (причем основанием его служит отрезок касатель­ной от точки касания до оси Оу).

Решение: Пусть у=f(х)—искомое уравнение кривой. Проведем касательную МN в произвольной точке М (х; у) кривой до пересечения с осью Оу в точке N (рис. 35). Согласно условию, должно выполняться равенство |ОN | = |ОМ|. Но |ОМ|= , а |ON| найдем из уравнения касательной У—у = y'(Х—х), полагая Х=0, т. е. У=|ОN|= =у—ху'.

Итак, приходим к однородному уравнению

Полагая у=tх, после замены и разделения переменных получим.

, или

откуда =C(C-2y)(семейство парабол, осью которых является ось Оу).

Подставляя координаты точки А в найденное общее решение, получим 0=С(С—2); из двух значений С=0и С=2 годится лишь второе, поскольку при С=0 парабола вырождается в ось Оу. Итак, искомой кривой является парабола x²=4(1-у), или у=1- x²/4.

548. Найти форму зеркала, собирающего все параллельные лучи в одну точку.

Решение: Очевидно, что зеркало должно иметь форму поверхности вращения, ось которой параллельна направлению падающих лучей. Примем эту ось за ось Ох и найдем уравнение кривой у=f(х), вращением которой образуется искомая поверхность.

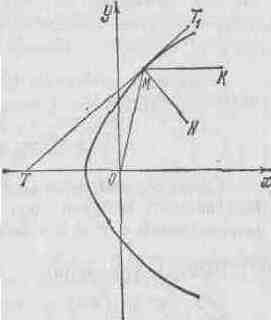
Начало координат поместим в точку, в которой собираются отраженные лучи. Обозначим падающий луч через КМ, а отраженный—через МО (рис. 36). Проведем касательную ТТ₁ и нормаль МN в точке М к искомой кривой.

Тогда треугольник ОМТ—равнобедренный с вершиной в точке О (так как ). Следовательно, |ОМ|=|OT|; но |OM|= , а |ОT| найдем из уравнения касательной У—у=у'(Х—х), полагая У=0; имеем Х=х-y/y’, откуда |ОT|=|Х|=—Х=-х+у/y’ . Таким образом, получаем дифференциальное уравнение

; или , т.е.

Рис. 35 Рис. 36

Это дифференциальное уравнение является однородным. Для его интегри­рования целесообразно ввести подстановку х=tу, принимая за аргумент у, а х (и t) за неизвестные функции этого аргумента. Тогда получим

, или

Разделяем переменные и интегрируем:

Отсюда , или возвращаясь к первоначальным переменным х и у, имеем

После упрощения находим окончательное решение в виде

Искомая кривая является параболой, а зеркало имеет форму параболоида вращения.

549. Найти ортогональные траектории семейства парабол х=ау² (а—параметр семейства).

Решение: Ортогональными траекториями данного семейства кривых называются такие кривые другого семейства, каждая из которых пересекает каждую из кривых первого семейства под прямым углом.

Если уравнение заданного семейства Р (х, у, а), то для отыскания орто­гональных траекторий нужно;

1) составить дифференциальное уравнение заданного семейства f(х, у, y')=0;

2) исходя из условия ортогональности y’_Iy’_II заменить в этом диф­ференциальном уравнении у' на —1/у';

3) проинтегрировать полученное уравнение f(х, у,—1/y')=0. Для реше­ния поставленной задачи дифференцируем уравнение заданного семейства парабол: 1=2ауу'. Исключая параметр семейства а из уравнений х=ау² и 1=2ауу', находим дифференциальное уравнение заданного семейства парабол:

2ху' =у. Заменяем y' на —1/у' и получаем дифференциальное уравнение семейства ортогональных траекторий:

2х-уу'=0, или 2хdх+уdу=0.

Интегрируя полученное уравнение, находим уравнение семейства ортого­нальных траекторий:

, или

Таким образом, ортогональными траекториями заданного семейства пара­бол являются подобные друг другу эллипсы, у которых большая полуось (вертикальная) в раз больше малой.

Решить уравнения:

550. ху' sin (у/х) + х = у sin (у/х).

551. ху+у²=(2х²+ху)у'.

552. ху'ln(у/х)=х+уln(у/х).

553. хуу'=у²+2х²

554. ху'—у=хtg(у/х); y(1)=π/2.

555. у'=(у/х)+соs(у/х).

556. у'=4+у/х+(у/х)²; у(1)=2.

557. (х²+у²)dх—хуdу=0.

558. у'=(х+у)/(х—у).

559. ху' = хе^y/x + y; y(1)=0.

560. ху'—у=x/ аrctg (y/х)

561. (х⁴+6х²у²+у⁴)dх+4ху(х²+у²)dy=0, у(1)=0.

562. ху'=2(у— ).

563. Зуsin(3х/у)dх+[у—3хsin(3х/у)]dу=0.

564. Найти кривую, у которой произведение абсциссы любой точки, принадлежащей кривой, на отрезок, отсекаемый нормалью на оси Ох, равно удвоенному квадрату расстояния этой точки от начала координат.

565. Найти ортогональные траектории семейства окружностей

4. Дифференциальные уравнения, приводящиеся к однородным. Уравне­ния вида

при приводятся к однородным подстановкой х=u+ , у= , где ( )—точка пересечения прямых =0 и =0. Если же , то подстановка позволяет разделить переменные.

566. Найти общий интеграл уравнения

(2х+у+1)dх+(х+2у—1)dу=0.

Решение: Уравнение принадлежит к первому типу, поскольку и ; Находим точку пересечения прямых 2x+y+1=0 и х+2у—1=0;

имеем х = = — 1; у = = 1.

Производим в исходном уравнении замену переменных, полагая х =u+ =u—1, y= = . Уравнение преобразуется к виду

(2и + ) du + (u + 2 )d = 0.

В полученном однородном уравнении положим =ut, откуда d =иdt+tdu; придем к уравнению с разделяющимися переменными

общий интеграл которого есть , или (после замены t= /u и возведения в квадрат)

u²+u + ²=С².

Возвращаясь к переменным х и у (и=х+1, =у—1), после элементар­ных преобразований найдем общий интеграл исходного уравнения

(здесь положено С1=С²—1).

567. Найти общий интеграл уравнения

(x+y+2)dx+(2x+2y-1)dy=0

Решение: Уравнение принадлежит ко второму типу, поскольку Положим поэтому y+x=t, dy=dt-dx. Данное уравнение примет вид

(t+2)dx+(2t-1)(dt-dx)=0 или (3-t)dx+(2t-1)dt=0

Разделяя переменные и интегрируя, имеем

или -2t-5ln|t-3|+x=-C

Возвращаясь к старым переменным (t=х+у), получим окончательный ответ:

х+2y+51п|x+у—3|=С.

Решить уравнения:

568. 2 (х + у) dу + (Зx + Зу— 1)dx = 0; у (0) = 2

569. (х—2у+3)dу+(2х+у—1)dх=0.

570. (х—у+4)dу+(x+у-2)dx=0.

571. Найти интегральную кривую дифференциального уравне­ния у'=(х+у-2)/(у-х-4), проходящую через точку Л1(1;1).

5. Дифференциальные уравнения в полных дифференциалах. Дифферен­циальное уравнение

Р(х, у)dх+Q(х, у)dy=0,

дР/дy= дQ/дx, называется уравнением в полных дифференциалах, т. е. левая часть такого уравнения есть полный дифференциал некоторой функции и (х, у) в односвязной области. Если это уравнение переписать в виде с1и==0, то его общее решение определяется равенством и=С. Функция и (х, у) может быть найдена по формуле

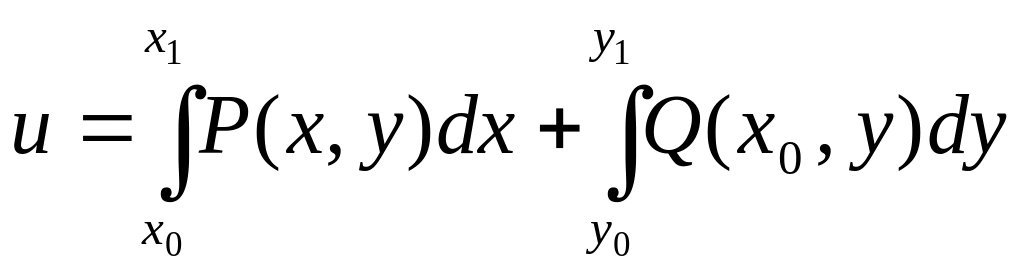
При этом в последней формуле нижние пределы интегралов ( и ) произвольны; их выбор ограничен единственным условием—интегралы в правой части этой формулы должны иметь смысл (т. е. не быть расходящимися несобственными интегралами второго рода). Если условие не выполняется, то в некоторых случаях можно привести рассматриваемое уравне­ние к указанному типу умножением его на так называемый интегрирующий множитель, который в общем случае является функцией от х и у: μ, (х, у). Если у данного уравнения существует интегрирующий множитель, зависящий только от х, то он находится по формуле

где отношение должно являться функцией только от х. Ана­логично, интегрирующий множитель, зависящий только от у, определяется по формуле

где должно являться функцией только от у (отсутствие в этих отношениях в первом случае у, а во втором х является признаком существования интегрирующего множителя рассматриваемого вида).

572. Найти общий интеграл уравнения

(е^х+у+siny)dx+( е^y+х+xcosy)dу=0.

Решение. Здесь Р(х, у)=е^х+уsinу, Q(х,у)= е^y+х+хсоsу, , . Следовательно, левая часть уравнения есть полный дифференциал некоторой функции и (х, у), т. е.

, .

Проинтегрируем по х:

Найдем функцию С (у), продифференцировав последнее выражение по y ,

Получаем уравнение

откуда находим С' (у) =еУ, т. е. С(у)==еУ. Таким образом, общий интеграл уравнения имеет вид е^х-\-х^|-\-х з1пу+еУ=С. ^

573. Найти общий интеграл уравнения

(х+у-1)dх+(е^у+х)dу=0.

Решение. Здесь Р(х, у)=х+у-1, Q(х, у)= е^у +х, , таким образом, условие полного дифференциала выполнено, т. е. данное уравнение является уравнением в полных дифференциалах. Найдем общий интеграл по формуле

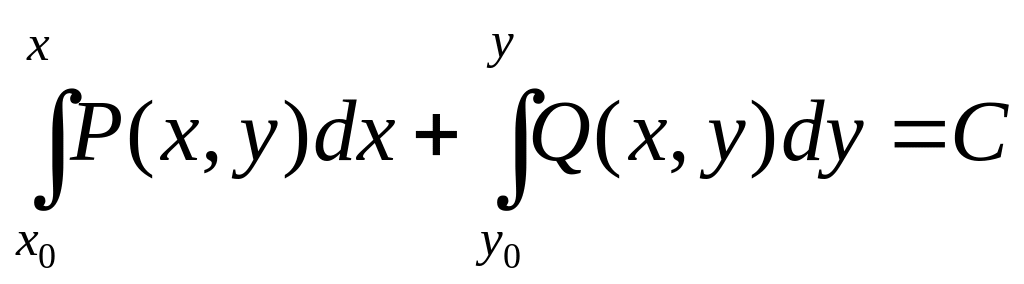
Взяв , получим

или

Подставляя пределы, находим , или , где

574. Найти общий интеграл уравнения

(x cosy-y siny)dy+(x siny+y cosy)dx=0.

Решение. Имеем

,

,

Поэтому данное уравнение имеет интегрирующий множитель, зависящий только от х. Найдем этот интегрирующий множитель:

Умножая исходное уравнение на е^x, получим уравнение

,

которое, как нетрудно убедиться, уже является уравнением в полных диффе­ренциалах; в самом деле, имеем Р₁(х, у) =е^х (xsiny+ycosy), Q₁ (х, у)= е^х (х соs у—у sinу). Отсюда

;

.

Эти производные равны и, следовательно, левая часть полученного уравнения имеет вид du (х, у). Таким образом,

.

Интегрируя первое из этих равенств по у, находим

.

Найдем производную по х от полученной, функции:

Сравнивая найденное значение с Р(x,y), получим С' (х)=0,т. е. С(х)=0.

Следовательно, общий интеграл исходного уравнения имеет вид

или .

Решить уравнения:

575. (x + siny)dх + (х соs у + sinу)dу = 0.

576. .

577. .

578. .

579. .

580. .

581. .

582. .

583. .

584. .

585. .

586. .

587. .

588. .

589. .

590.

Проинтегрировать следующие уравнения, имеющие интегри­рующий множитель, зависящий только от х или только от у:

591. .

592. .

593. .

594. .

595. Доказать, что уравнение Р(х,у)dx+Q(х,y)dy=0, кото­рое одновременно является и однородным, и уравнением в полных дифференциалах, имеет общий интеграл Рх+Qу=С.

● Воспользоваться теоремой Эйлера об однородных функциях, согласно которой , где t—показатель однородности функций Р(х,у) и Q(х,y).