- •Глава IV
- •§ 1. Дифференциальные уравнения первого порядка
- •6. Линейные дифференциальные уравнения первого порядка. Уравнения
- •§ 2. Дифференциальные уравнения высших порядков
- •§ 3. Линейные уравнения высших порядков
- •3. Линейные однородные уравнения с постоянными коэффициентами.
- •Постоянные с1 и с2 найдем, используя краевые условия. Имеем
- •§ 4. Интегрирование дифференциальных уравнений с помощью рядов
- •§ 5. Системы дифференциальных уравнений
§ 4. Интегрирование дифференциальных уравнений с помощью рядов
1. Применение рядов к решению дифференциальных уравнений. В некоторых случаях, когда интегрирование дифференциального уравнения в элементарных функциях невозможно, решение такого уравнения ищут в виде степенного ряда
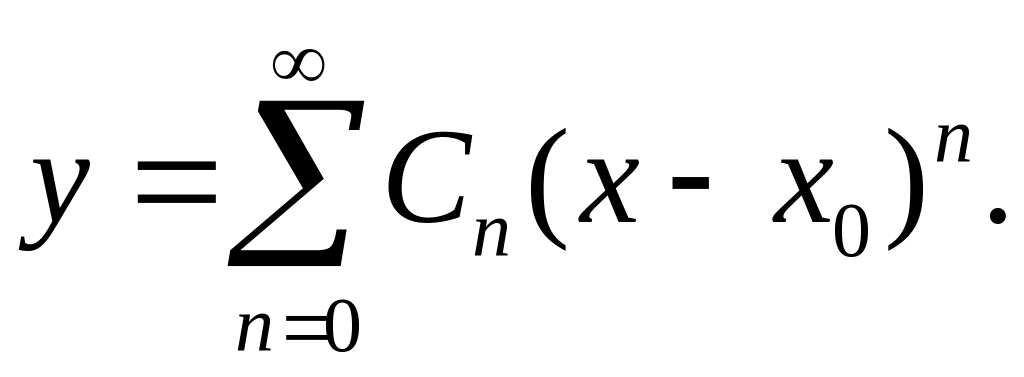
Неопределенные
коэффициенты
![]() находят подстановкой ряда в уравнение
и приравниванием коэффициентов при
одинаковых степенях разности
находят подстановкой ряда в уравнение
и приравниванием коэффициентов при
одинаковых степенях разности
![]() в обеих частях полученного равенства.
Если удается найти все коэффициенты
ряда, то полученный ряд определяет
решение во всей своей
в обеих частях полученного равенства.
Если удается найти все коэффициенты
ряда, то полученный ряд определяет
решение во всей своей
области сходимости.
В тех случаях,
когда длу уравнения![]() требуется решить задачу Коши при
начальном условии
требуется решить задачу Коши при
начальном условии
![]() решение можно искать с помощью ряда
Тейлора:
решение можно искать с помощью ряда
Тейлора:
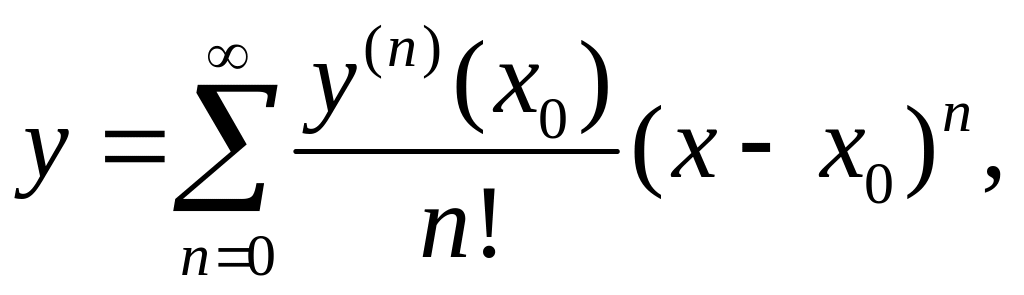
где
![]()
![]() ,
а дальнейшие производные
,
а дальнейшие производные
![]() находят последовательным дифференцированием
исходного уравнения и подстановкой в
результат дифференцирования вместо
находят последовательным дифференцированием
исходного уравнения и подстановкой в
результат дифференцирования вместо
![]() значений
значений
![]() и всех остальных найденных последующих
производных. Аналогично с помощью ряда
Тейлора можно интегрировать и уравнения
высших порядков.
и всех остальных найденных последующих
производных. Аналогично с помощью ряда
Тейлора можно интегрировать и уравнения
высших порядков.
756.
Проинтегрировать уравнение![]()
Δ Будем искать решение этого уравнения в виде ряда
![]()
Подставляя у и у" в исходное уравнение, находим
![]()
![]()
Сгруппируем члены с одинаковыми степенями х:
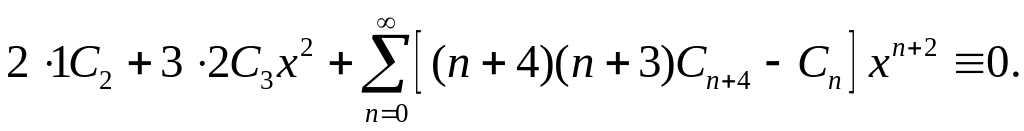
Приравнивая нулю все коэффициенты полученного ряда (чтобы уравнение обратилось в тождество), находим
![]()
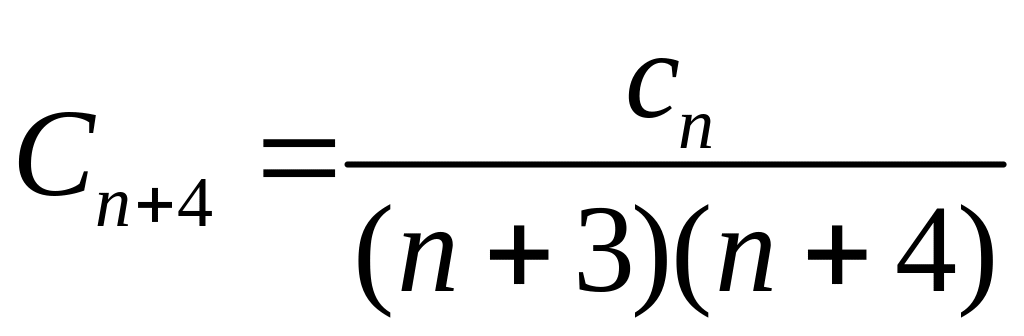
![]()
Последнее соотношение позволяет найти последовательно все коэффициенты искомого разложения (Со и С1 остаются произвольными и играют роль произвольных постоянных интегрирования);
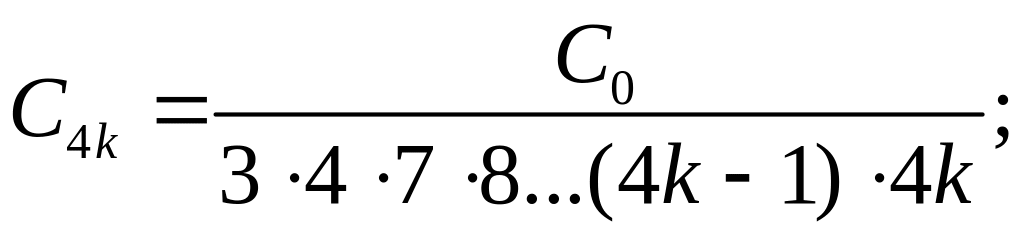
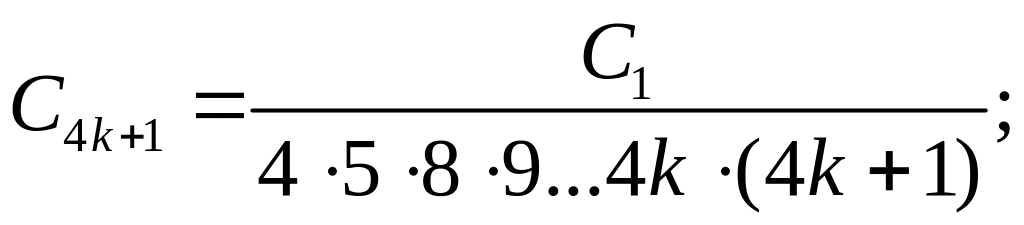
![]()
![]()
Таким образом,
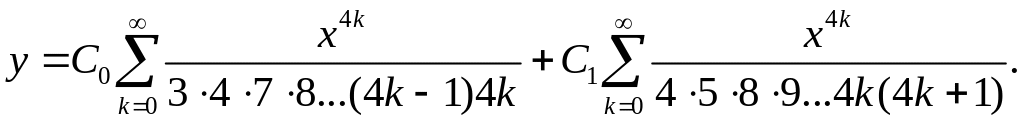
Полученные ряды сходятся на всей числовой оси и определяют два линейно независимых частных решения исходного уравнения. ▲
С помощью разложения в ряд по степеням х проинтегрировать следующие уравнения н определить область существования полученного решения:
757.
![]()
758.
![]()
ф В силу начального условия положить Со==0.
759. у"+ху'+у=0.
760. у"—ху'—2у=0.
761.
![]()
● В силу начальных условий положить Со=0, С1=1.
762.
Проинтегрировать приближенно с помощью
ряда Тейлора уравнение
![]()
![]() взяв шесть первых членов разложения,
отличных от нуля.
взяв шесть первых членов разложения,
отличных от нуля.
Δ
Из уравнения начальных условий находим
![]() Дифференцируя данное уравнение,
последовательно получаем
Дифференцируя данное уравнение,
последовательно получаем
![]()
![]()
![]()
![]()
Полагая
х=0 и
используя значения
![]() последовательно находим
последовательно находим
![]()
![]()
![]()
![]() Искомое решение имеет вид
Искомое решение имеет вид
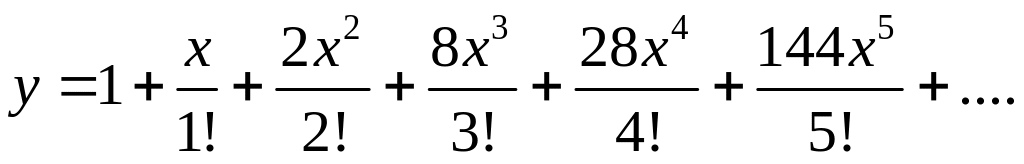 ▲
▲
763.
![]()
![]()
![]() Найти четыре первых (отличных от нуля)
члена разложения.
Найти четыре первых (отличных от нуля)
члена разложения.
. Δ
Дифференцируя уравнение
![]() имеем
имеем
![]()
![]()
![]()
![]()
При х=0 получаем
у(0)=0,
у'(0)=1,
![]()
![]()
![]()
![]()
![]()
Решение имеет вид
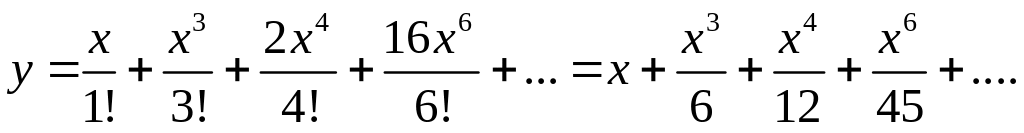 ▲
▲
764.
![]()
![]() Найти четыре
первых (отличных от нуля) члена разложения.
Найти четыре
первых (отличных от нуля) члена разложения.
765.
![]()
![]() Найти два первых (отличных от нуля) члена
разложения.
Найти два первых (отличных от нуля) члена
разложения.
766.
![]() Найти четыре первых (отличных от
нуля) члена разложения.
Найти четыре первых (отличных от
нуля) члена разложения.
767.
![]()
![]() Найти точное
решение.
Найти точное
решение.
768.
![]() Найти пять
первых членов разложения.
Найти пять
первых членов разложения.
769.
![]() Найти пять
первых членов разложения.
Найти пять
первых членов разложения.
2. Уравнение Бесселя. Линейное дифференциальное уравнение с переменными коэффициентами, имеющее вид
![]() (1)
(1)
называется
уравнением
Бесселя (к
этому же виду сводится уравнение
![]() заменой
заменой
![]() ),
),
Решение уравнения (1) будем искать в виде обобщенного степенного ряда, т. е. произведения некоторой степени х на степенной ряд:
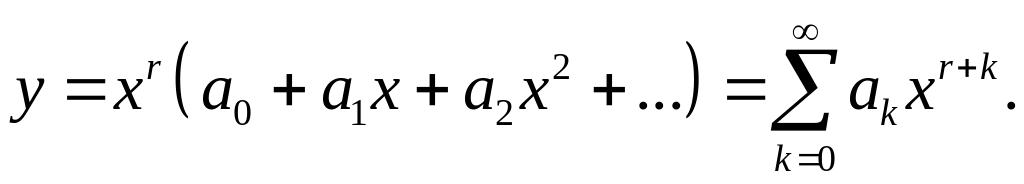 (2)
(2)
Подставляя обобщенный степенной ряд в уравнение (1) и приравнивая нулю коэффициенты при каждой степени х в левой части уравнения, получим систему
ФОРМУЛА………………….
Считая, что
![]() из данной системы находим
из данной системы находим
![]() Пусть
Пусть
![]() Тогда из второго уравнения системы
находим
Тогда из второго уравнения системы
находим
![]() а из уравнения
а из уравнения
![]() придавая k
значения 3, 5, 7, ... , заключаем, что
придавая k
значения 3, 5, 7, ... , заключаем, что
![]() Дяя коэффициентов с четными номерами
получаем выражения
Дяя коэффициентов с четными номерами
получаем выражения
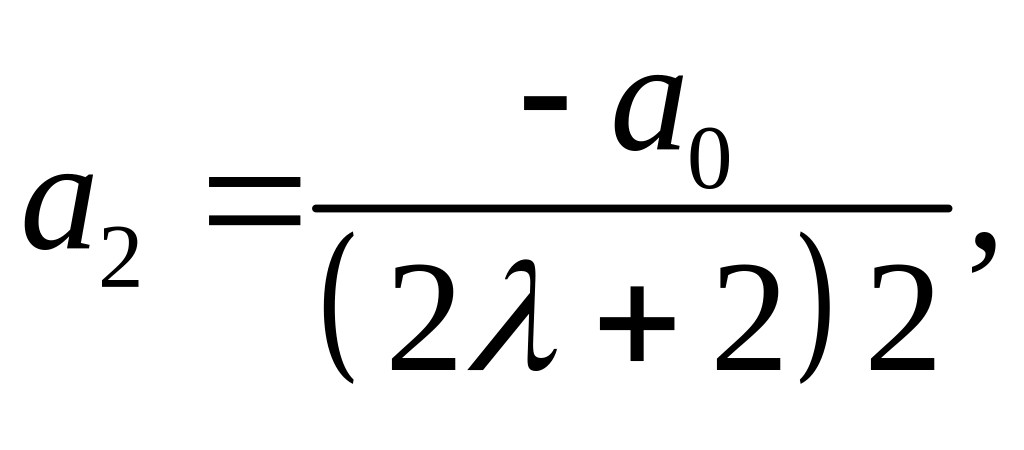
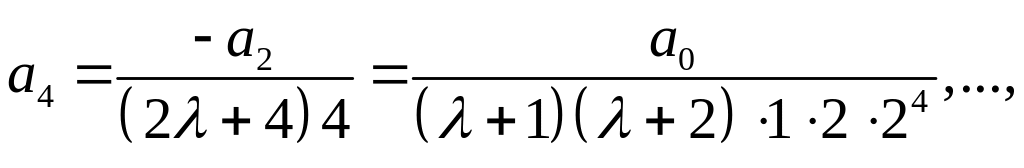

Подставляя найденные коэффициенты в ряд (2), получим решение
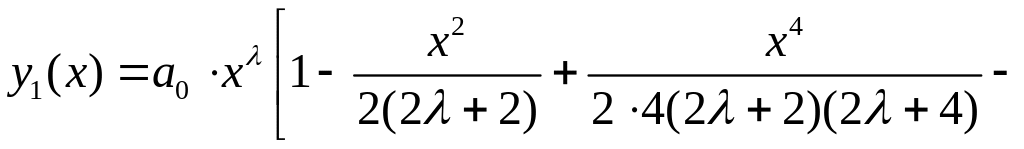
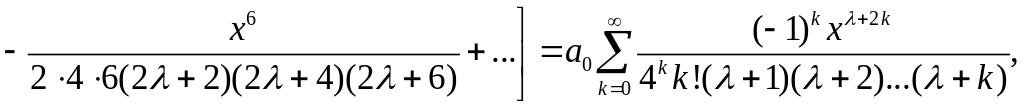
где коэффициент
![]() остается произвольным.
остается произвольным.
При
![]() все коэффициенты ад аналогично
определяются только в случае, когда
все коэффициенты ад аналогично
определяются только в случае, когда
![]() не равно целому числу. Тогда решение
можно получить, заменяя в предыдущем
решении
не равно целому числу. Тогда решение
можно получить, заменяя в предыдущем
решении![]() величину
на —
:
величину
на —
:
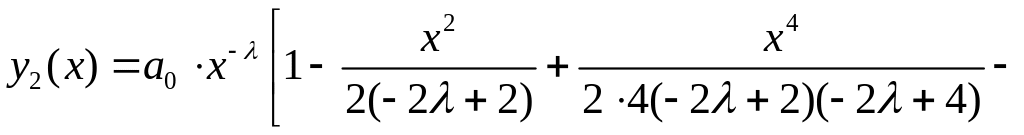
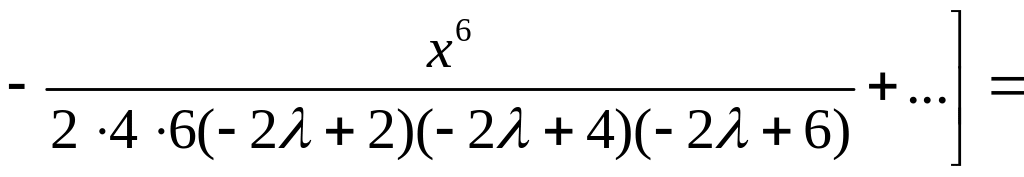
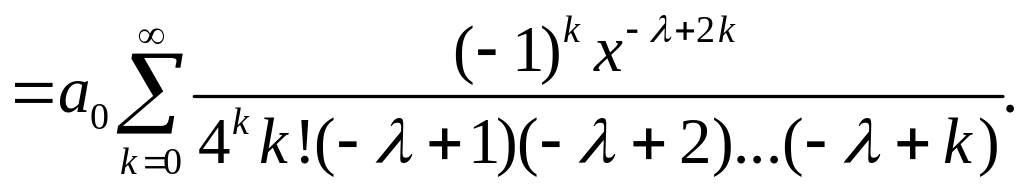
Полученные степенные ряды сходятся для всех значений х, что легко устанавливается на основании признака Даламбера. Решения у1 (х) и y2(х) линейно независимы, так как их отношение не является постоянным.
Решение у1(х),
умноженное на постоянную
 называется функцией
Бесселя (или
цилиндрической
функцией) порядка
λ первого
рода и
обозначается символом
называется функцией
Бесселя (или
цилиндрической
функцией) порядка
λ первого
рода и
обозначается символом
![]() Решение у2
обозначают
Решение у2
обозначают
![]()
Следовательно, общее решение уравнения (1) при λ, не равном целому чгслу, имеет вид
![]()
где C1 и С2—произвольные постоянные величины.
В общепринятом
выборе постоянной
участвует
гамма-функция
![]() ,
которая определяется несобственным
интегралом (см. с. 35):
,
которая определяется несобственным
интегралом (см. с. 35):
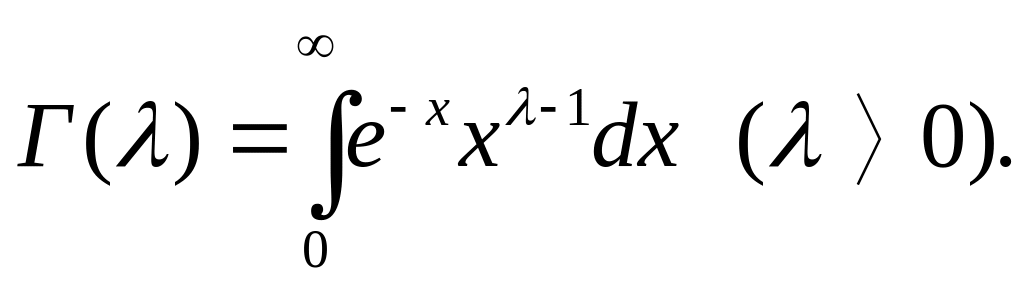
Можно показать, что при λ, равном половине нечетного числа, функция Бссселя выражается через элементарные функции, так как в этом случае гамма-функция, входящая в определение функции Бесселя
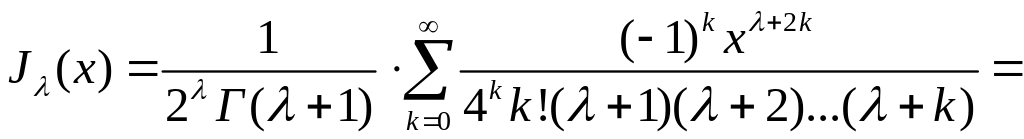
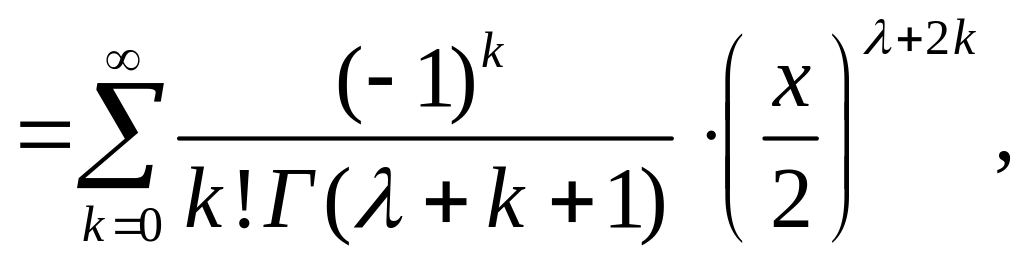
[произведение
![]() заменено, согласно свойству гамма-функции,
на
заменено, согласно свойству гамма-функции,
на![]() ],
принимает следующие значения:
],
принимает следующие значения:

(здесь использовано значение интеграла Пуассона);
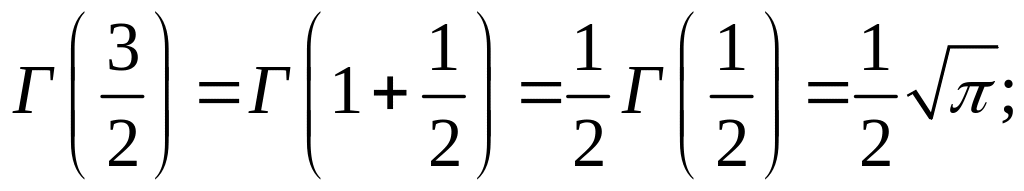
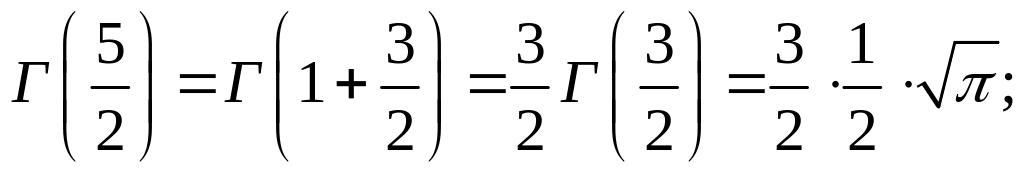

Функцию Бесселя
![]() (натуральном) можно записать так:
(натуральном) можно записать так:

Для отрицательного и целого λ частное решение не выражается функцией Бесселя первого рода и его следует искать в форме
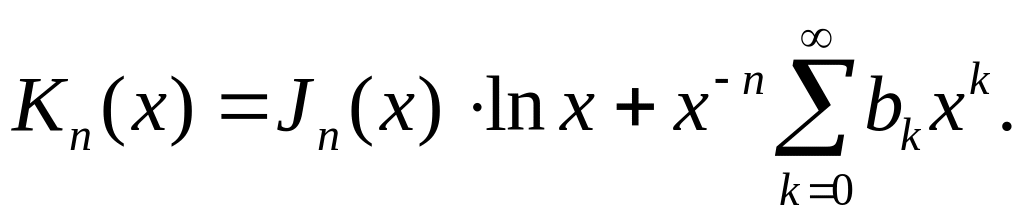
Подставляя это
выражение в уравнение (1), мы определим
коэффициенты
![]() .
Функция
.
Функция
![]() умноженная на некоторую постоянную,
называется функ-цией
Бесселя п-го порядка второго рода.
умноженная на некоторую постоянную,
называется функ-цией
Бесселя п-го порядка второго рода.
770.
Найти функцию Бесселя при
![]()
Δ Воспользовавшись равенством
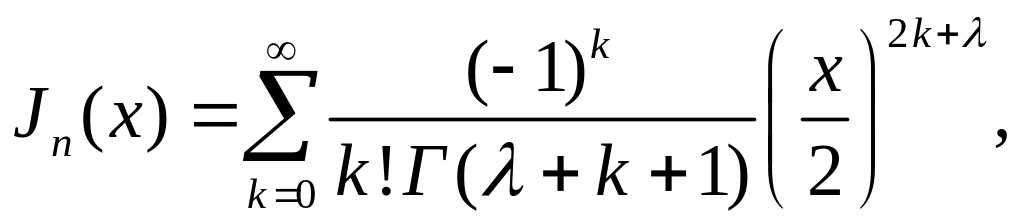
при
![]() получим
получим
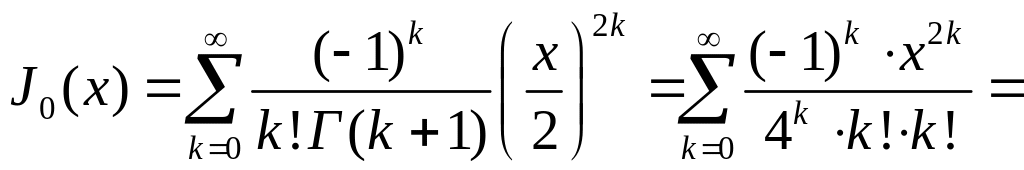
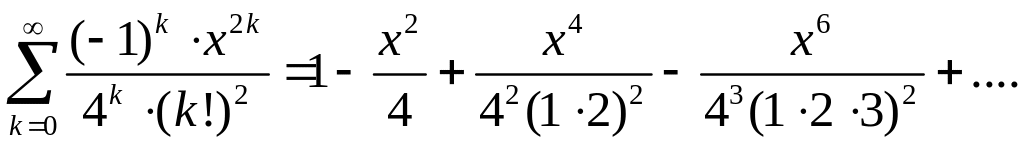 ▲
▲
771.
Решить уравнение
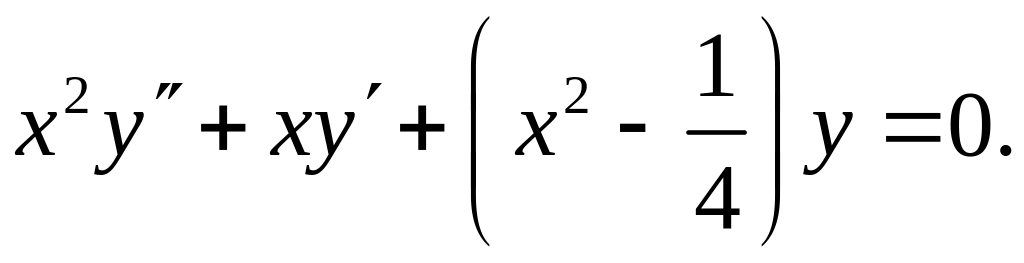
Δ
Так как
![]() то общее решение уравнения имеет вид
то общее решение уравнения имеет вид
![]() где
где
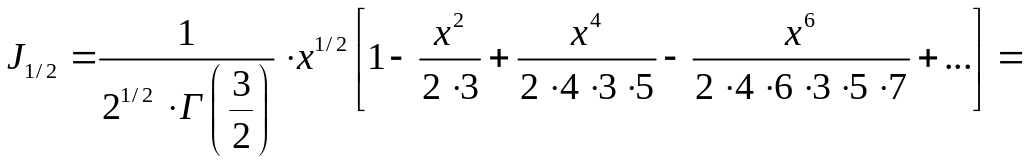
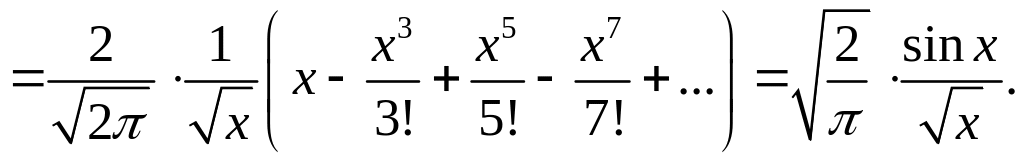
Точно так же получим
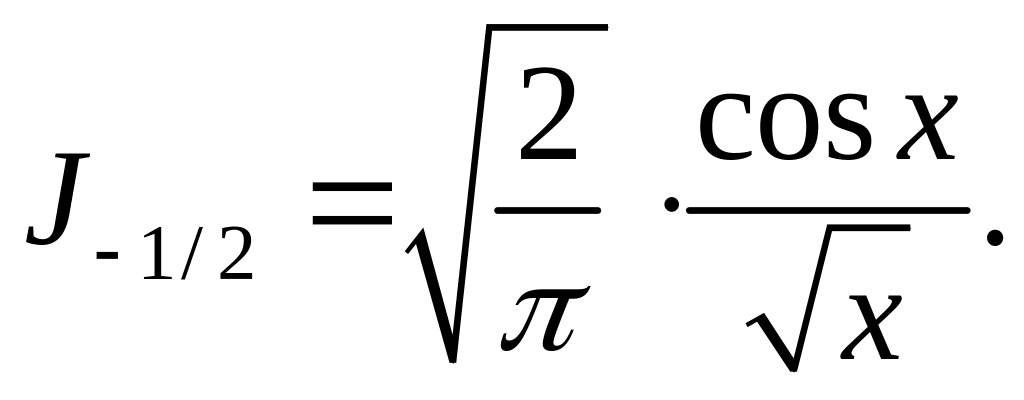 Следовательно, общее решение
Следовательно, общее решение
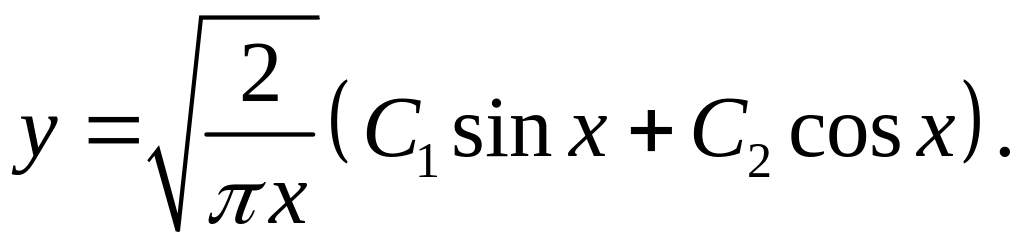 ▲
▲
772.
Найти
![]()
773.
Решить уравнение
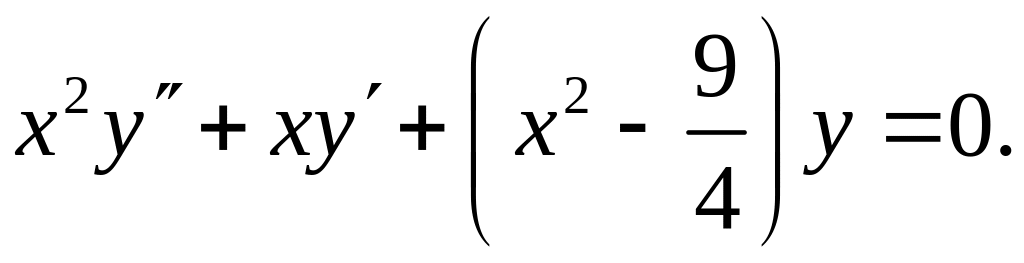
774.
Решить уравнение