3. Линейные однородные уравнения с постоянными коэффициентами.

Ли­нейным однородным уравнением п-го порядка с постоянными коэффициен­тами называется уравнение вида

(1)

где коэффициенты — некоторые действительные числа. Для нахождения частных решений уравнения (1) составляют характеристическое уравнение

(2)

которое получается из уравнения (1) заменой в нем производных искомой функции соответствующими степенями k, причем сама функция заменяется единицей. Уравнение (2) является уравнением n-й степени и имеет п корней . (действительных или комплексных, среди которых могут быть и равные).

Тогда общее решение дифференциального уравнения (1) строится в зави­симости от характера корней уравнения (2):

1) каждому действительному простому корню и в общем решении соответ­ствует слагаемое вида ;

2) каждому действительному корню кратности т в общем решении соответствует слагаемое вида ;

3) каждой паре комплексных сопряженных простых корней и в общем решении соответствует слагаемое вида ;

4) каждой паре комплексных сопряженных корней и кратности т в общем решении соответствует слагаемое вида .

689. Найти общее решение уравнения у"—7у'+6y=0.

Решение. Составим характеристическое уравнение ; его корни . Следовательно, е^6x и e^х—частные линейно независимые решения, а общее решение имеет вид

690. Найти общее решения уравнения .

Решение. Характеристическое уравнение имеет вид ; его корням соответствуют линейно независимые частные решения е^3x, е^-3x, е^2x и е^-2x. Следовательно, общее решение

691. Найти решение уравнения , удовлетворяю­щее начальным условиям х=0, при t=0.

Решение. Характеристическое уравнение k² – k – 2=0 имеет корни . Следовательно, общее решение . Подставляя начальные условия в общее решение и его производную, получим систему уравнений относительно и :

откуда =1, = -1. Значит, решение, удовлетворяющее поставленным на­чальным условиям, имеет вид

692. Найти решение уравнения , удовлетворяющее краевым условиям х=0 при t=0 и x=3 при t=ln2.

Решение. Характеристическое уравнение k²—2k=0 имеет корни . Следовательно, общее решение записывается в виде . Подставляя краевые условия в найденное общее решение, получаем

или

Отсюда = -1, =1. Итак, х=е^2х—1—искомое частное решение, удовлетворяющее заданным краевым условиям.

693. Найти общее решение уравнения .

Решение. Характеристическое уравнение k³ –2k² + k=0 имеет корни . Здесь 1 является двукратным корнем, а поэтому линейно независи­мыми частными решениями служат . Общее решение имеет вид

694. Найти общее решение уравнения .

Решение. Характеристическое уравнение имеет корни . Корни характеристического уравнения комплексные сопряженные, а потому им соответствуют частные решения е^2x соs Зх и e^2x sin Зх. Следовательно, об­щее решение есть

695. Материальная точка массы т движется по оси Ох под действием восстанавливающей силы, направленной к началу ко­ординат и пропорциональной расстоянию движущейся точки от начала; среда, в которой происходит движение, оказывает дви­жению точки сопротивление, пропорциональное скорости движе­ния. Найти закон движения.

Решение. Пусть —скорость точки; —ее ускорение; на точку действуют две силы: восстанавливающая и сила сопротивления среды , Согласно второму закону Ньютона, имеем

, или .

Мы получили линейное однородное дифференциальное уравнение второго по­рядка. Его характеристическое уравнение имеет корни

1) Если b²—4та > 0, то корни — действительные, различные и оба отри­цательные; вводя для них обозначения

,

находим общее решение уравнения движения в виде

(это—случай так называемого апериодического движения).

2) Если , то корни характеристического уравнения—действительные равные:

.

В этом случае общее решение уравнения движения имеет вид

.

3) Наконец, если b²—4та < 0, то характеристическое уравнение имеет комплексные сопряженные корни:

,

где

.

Общее решение уравнения движения имеет вид

или

где

(затухающие колебания).

Найти общие решения уравнений:

696. . 697. .

698. . 699. .

700. . 701.

702. .

Найти решения уравнений, удовлетворяющие заданным на­чальным или краевым условиям:

703. .

704. .

705. .

706. .

707. .

708. .

709. .

710. Решить задачу 695, если сила сопротивления среды равна нулю.

4. Линейные неоднородные уравнения. Структура общего решения линей­ного неоднородного уравнения, т. е. уравнения с правой частью:

,

определяется следующей теоремой.

Если u=u(x) — частное решение неоднородного уравнения, а — фундаментальная система решений соответствующего однородного уравнения, то общее решение линейного неоднородного уравнения имеет вид иными словами, общее решение неоднородного уравнения равно сумме любого его частного решения и общего решения соответствую­щего однородного уравнения.

Следовательно, для построения общего решения неоднородного уравнения надо найти одно его частное решение (предполагая уже известным общее ре­шение соответствующего однородного уравнения).

Рассмотрим два метода отыскания частного решения линейного неодно­родного уравнения.

Метод вариации произвольных постоянных. Этот метод применяется для отыскания частного решения линейного неоднородного урав­нения п-ого порядка как с переменными, так и с постоянными коэффициен­тами, если известно общее решение соответствующего однородного уравнения.

Метод вариации заключается в следующем. Пусть известна фундамен­тальная система решений соответствующего однородного урав­нения. Тогда общее решение неоднородного уравнения следует искать в виде

где функции определяются из системы уравнений

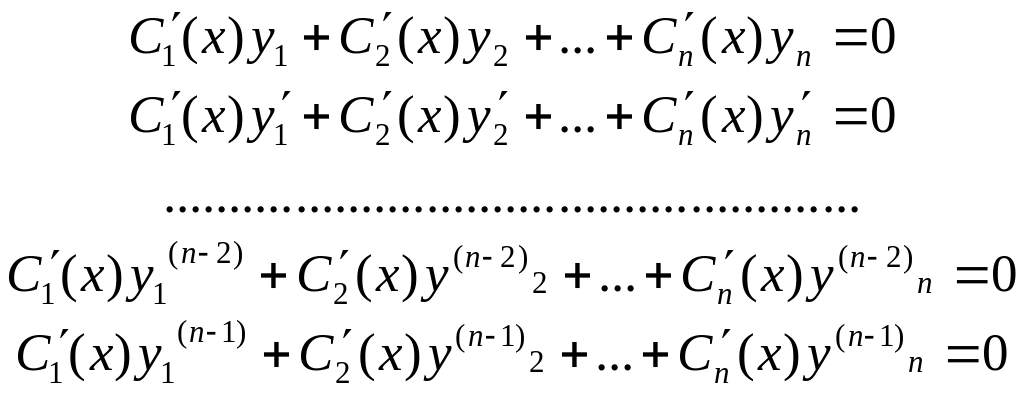
[f(х)—правая часть данного уравнения].

Для уравнения второго порядка соответствую­щая система имеет вид

Решение этой системы находится по формулам

в силу чего u(х) можно сразу определить по формуле

(здесь —вронскиан решений и )

Пусть, например, требуется проинтегрировать уравнение

Для соответствующего однородного уравнения мы нашли частные решения

и (см. с. 146); их вронскиан .

УГ

Поэтому u(х) можно найти по формуле

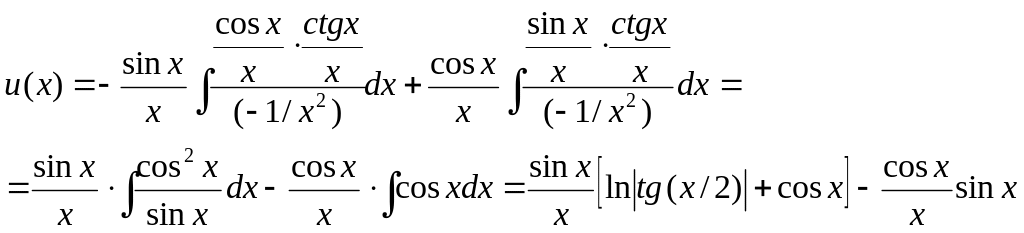
Таким образом, , а общее решение данного урав­нения имеет вид

.П р и м е ч а н и е. Еще раз отметим, что линейное неоднородное уравнение второго порядка может быть проинтегрировано в квадратурах, если известно одно частное решение соответствующего однородного уравнения; общее решение такого уравнения имеет вид , где определя­ется через по формуле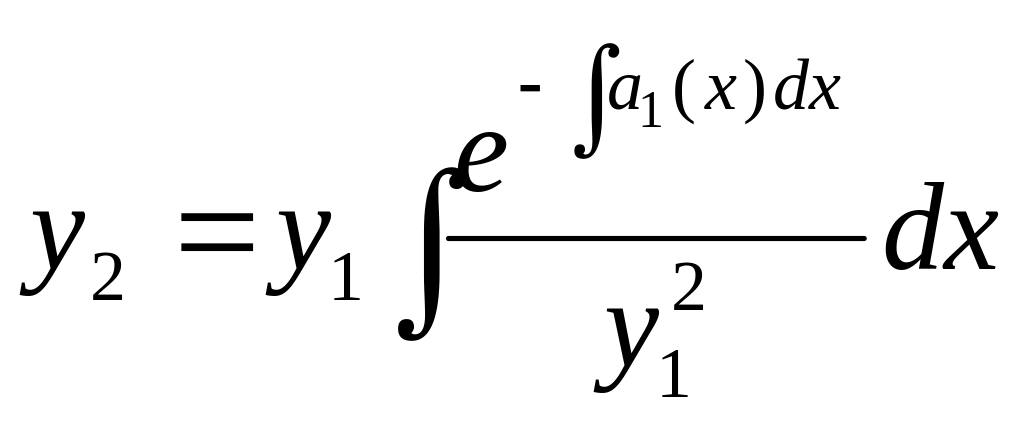

а и (х) определяется через и по вышеприведенной формуле.

Метод подбора частного решения метод неопределен­ных коэффициентов. Этот метод применим только к линейным урав­нениям с постоянными коэффициентами и только в том случае, когда его пра­вая часть имеет следующий вид:

(или является суммой функций такого вида). Здесь α и β—постоянные, и —многочлены от х соответственно n-й и т-й степени. Частное решение уравнения n-го порядка

(где f(х) имеет указанный вид, а действительные постоянные коэффициенты) следует искать в виде

.

Здесь r равно показателю кратности корня в характеристическом уравнении (если характеристическое уравнение та­кого корня не имеет, то следует положить r=0); и —полные мно­гочлены от х степени l с неопределенными коэффициентами, причем l равно наибольшему из чисел п и m (l = n ≥ m, или l = m ≥ n):

.

Подчеркнем, что многочлены и должны быть полными (т. е. содержать все степени х от нуля до l), с различными неопределенными коэффициентами при одних и тех же степенях х в обоих многочленах и что при этом, если в выражение функции f(х) входит хотя бы одна из функций или , то в и (х) надо всегда вводить обе функции.

Неопределенные коэффициенты можно найти из системы линейных алгеб­раических уравнений, получаемых отождествлением коэффициентов подобных членов в правой и левой частях исходного уравнения после подстановки в него

м(х) вместо у.

Проверку правильности выбранной формы частного решения дает сопо­ставление всех членов правой части уравнения с подобными им членами левой части, появившимися в ней после подстановки и (х).

Если правая часть исходного уравнения равна сумме нескольких различ­ных функций рассматриваемой структуры, то для отыскания частного решения такого уравнения нужно использовать теорему наложения решений: надо найти частные решения, соответствующие отдельным слагаемым правой части, и взять их сумму, которая и является частным решением исходного уравнения (т. е. уравнения с суммой соответствующих функций в правой части).

П р и м е ч а н и е. Частными случаями функции f(х) рассматриваемой структуры (при наличии которых в правой части уравнения применим метод подбора частного решения) являются следующие функции:

1) , А—постоянная .

2) , А и В—постоянные .

3) (многочлен степени п) .

4) .

5) .

6) , А и B—постоянные.

711. Найти частное решение уравнения у"—2у'—Зу=е^4х, удовлетворяющее краевым условиям .

Решение. Характеристическое уравнение имеет корни . Общее решение соответствующего однородного уравнения . Частное решение исходного уравнения следует искать в виде (так как в правой части отсутствуют синус и косинус, коэффициентом при показательной функции служит многочлен нулевой степени, т. е. 1=п=0, и r=0, поскольку α=4 не является корнем характеристического уравнения).

Итак,

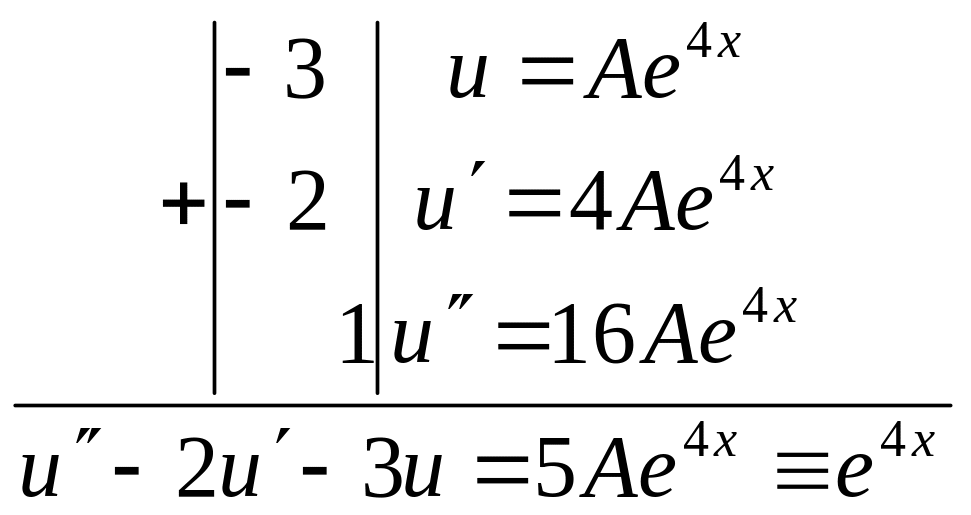
Таким образом, A =1/5. Следовательно, общее решение данного уравнения

Для нахождения и воспользуемся краевыми условиями:

или

Отсюда = - 491/600, = 652/75. Итак,

712. Проинтегрировать уравнение при начальных условиях .

Решение. Характеристическое уравнение имеет корни , а потому общее решение однородного уравнения . Частное решение неоднородного уравнения следует искать в виде

(в данном случае α=0, β=1, ; поскольку такого корня у характе­ристического уравнения нет, то r=0; т=п=0, а следовательно, и l=0).

Итак,

.

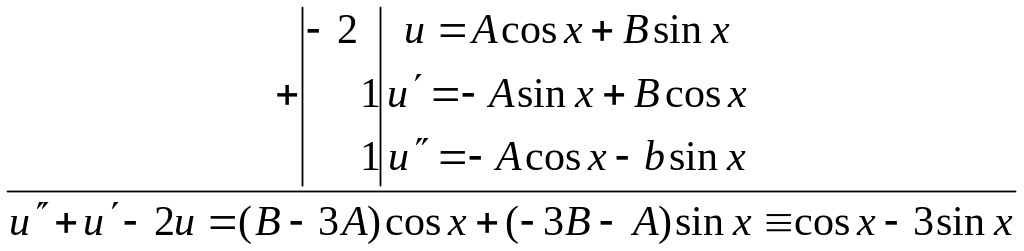Таким образом, имеем систему

т.е. A=0, B=1

Следовательно, общее решение данного уравнения имеет вид

Найдем и , используя; начальные условия:

или

Отсюда , , т. е.

713. Проинтегрировать уравнение при началь­ных условиях у(0)=у'(0)=0.

Решение. Характеристическое уравнение имеет корни k₁=0, k₂=1. Общее решение однородного уравнения Частное решение неодно­родного уравнения в данном случав можно искать в виде Дифференцируя и подставляя в исходное уравнение, получим:

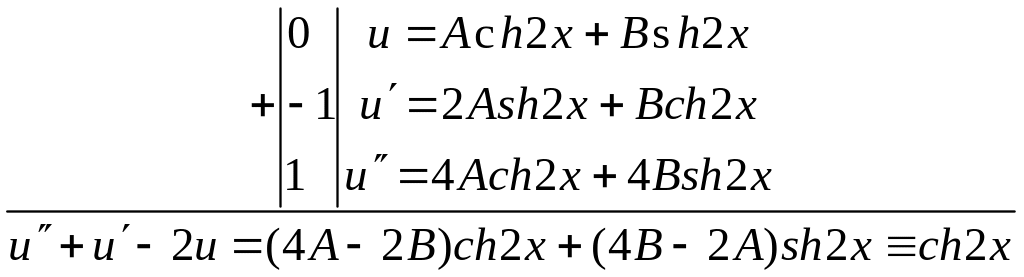
Таким образом,

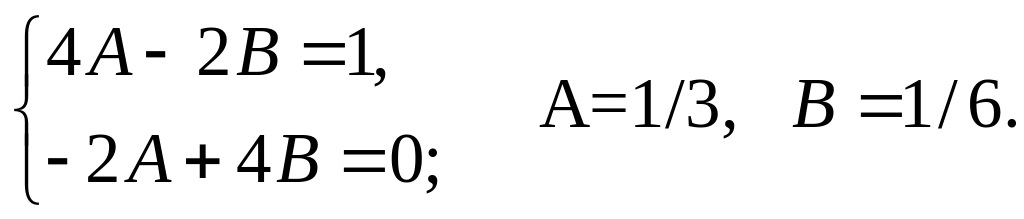
Значит, общее решение исходного уравнения имеет вид

Для нахождения С₁ и С₂ используем начальные условия:

Cледовательно, Итак, искомое частное решение имеет вид

▲

Примечание. Согласно, общей теории мы должны были бы правую часть заданного уравнения представить в виде и применить теорему наложения, т. е. искать отдельно решения, соответствующие слагае­мым и правой части. Мы имели бы:

для таким образом,

для таким образом,

Поэтому частное решение следовало искать в виде

но

Именно в этом виде мы и искали решение данного уравнения.

Вообще следует заметить, что при изменении метода подбора частного решения последнее всегда отыскивается в виде функции такой же структуры, как и правая часть заданного уравнения, но при этом целесообразно допол­ненной добавочными слагаемыми и множителями, чтобы обеспечить возмож­ность отождествления полученных после подстановки в левую часть уравне­ния членов со всеми (подобными им) членами правой части.

714. Решить уравнение

∆ Характеристическое уравнение имеет корни а потому общее решение однородного уравнения Част­ное решение следует искать в виде (в данном случае так как 0 не является корнем характеристического уравне­ния, то ). Итак,

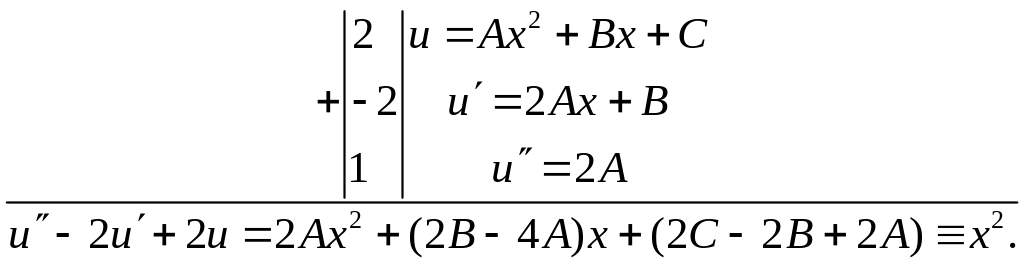
Отсюда Следовательно, общее решение исходного уравнения

▲

715. Решить уравнение

∆ Характеристическое уравнение имеет корни по­этому общее решение однородного уравнения Пользуясь принципом наложения, частное решение исходного уравнения будем искать в виде (имеем для поскольку такого корня нет, для ). Итак,

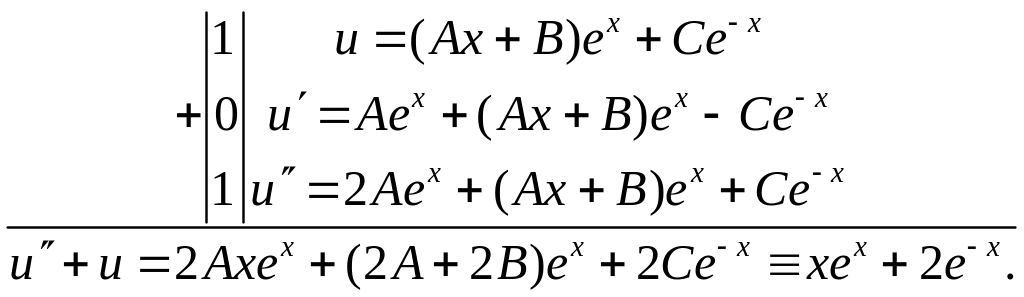
Отсюда Следовательно, общее решение исходного уравнения

716. Решить уравнение у'"+у"—2у'=х—e^x.

 Характеристическое уравнение имеет корни а потому общее решение однородного уравнения Частное решение ищем, пользуясь принципом наложения, в виде Итак,

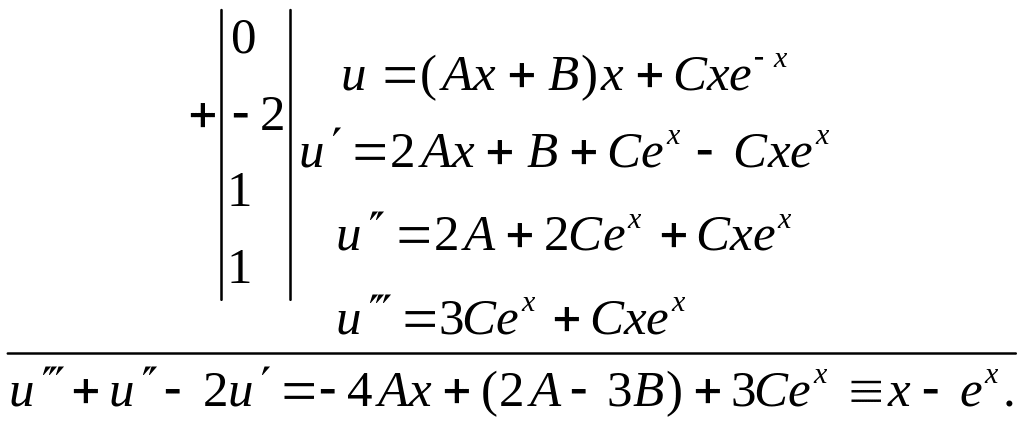
Отсюда т.е. . Следовательно, общее решение исходного уравнения

▲

717. Найти решение уравнения у" + у = 3sinх, удовлетворяю­щее краевым условиям

Д Характеристическое уравнение имеет корни а по­тому общее решение однородного уравнения Частное решение следует искать в виде (в данном случае , так как i является простым корнем характеристического уравнения, то ). Итак,

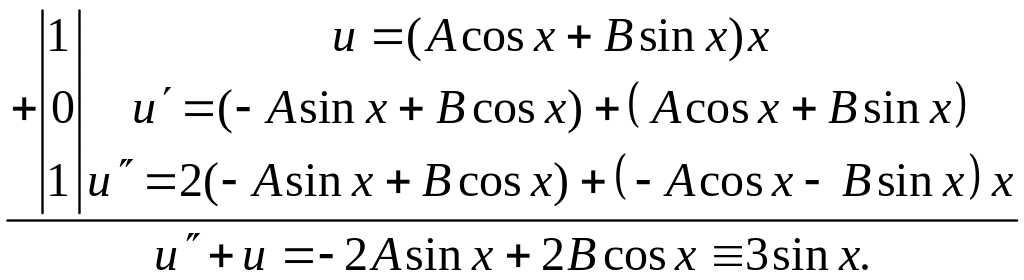
Отсюда 2B=0, т.е. A= -3/2, B=0. Следовательно, общее решение исходного уравнения