
- •Зразки розв’язування задач.
- •4. Рівняння площини у відрізках на осях
- •3.5. Пряма в просторі
- •3.5.1. Рівняння прямої в просторі
- •3.5.2. Кут між двома прямими в просторі. Умови паралельності та перпендикулярності
- •3.5.3. Кут між прямою і площиною. Умови паралельності та перпендикулярності прямої і площини
- •24.Функція,способи задання,область визначення та область значень.Елементарні функції та її графіки.
- •Означення показникової функції.
- •Задачі, які приводять до поняття показникової функції.
- •3. Побудова графіка показникової функції.
- •Властивості показникової функції.
- •Перетворення графіків функцій
- •Зразки розв’язування задач
- •Інтегрування раціональних дробів
1.Визначники.Методи обчислення визначників.
. Визначником (детермінантом) квадратної матриці A=(aij) називається алгебраїчна сума всіх можливих добутків елементів матриці, взятих по одному з кожного рядка і кожного стовпця
Вираз
Δ =
 =
=
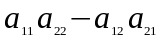 називається визначником
(
детермінантом
) другого
порядку.
називається визначником
(
детермінантом
) другого
порядку.
Δ
− дельта,
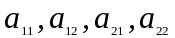 −
елементи
визначника.
−
елементи
визначника.
Поняття „ визначник „ ( від латинського determino − визначаю ) ввів німецький математик Вільгельм Лейбніц ( 1646 − 1716 ).
Вираз
Δ =
 =
=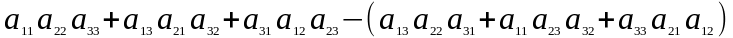
називається визначником третього порядку.
а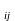 −
елемент визначника, ij
− індекси,
−
елемент визначника, ij
− індекси,
i − номер рядка,
j − номер стовпця.
Визначник третього порядку обчислюється за правилом трикутника:
Δ
=
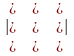 =
+
+
−
=
+
+
−
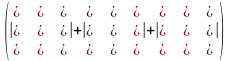 ,
,
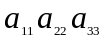 − елементи
головної діагоналі,
− елементи
головної діагоналі,
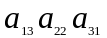 − елементи
побічної діагоналі.
− елементи
побічної діагоналі.
Елементами визначника можуть бути не тільки числа, а й алгебраїчні чи тригонометричні вирази,функції тощо.
Приклад.
Обчислити визначники:
а).
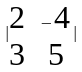 = 2·5
− 3·( -4 ) = 10 + 12 = 22;
= 2·5
− 3·( -4 ) = 10 + 12 = 22;
б).
 =
=
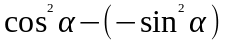 =
=
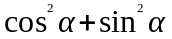 = 1;
= 1;
в).
 = −12 + 40 + 3
− ( −8
+ 4 + 45
) = 31
− 41 = −10.
= −12 + 40 + 3
− ( −8
+ 4 + 45
) = 31
− 41 = −10.
Властивості визначників.
1). Визначник не змінюється, якщо:
 його
рядки замінити відповідними стовпцями
:
його
рядки замінити відповідними стовпцями
:
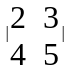 =
=
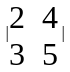 ;
;
якщо до елементів одного рядка ( стовпця ) додати відповідні елементи іншого рядка ( стовпця ) помножені на одне й те саме число:
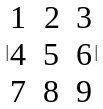 =
=
 .
.
2). Визначник дорівнює нулю, якщо:
один з рядків ( стовпців ) визначника складається тільки з нулів;
визначник має два однакових рядки ( стовпці );
у визначнику елементи двох рядків ( стовпців ) пропорційні.
3). Якщо переставити місцями два рядки ( стовпці ), то визначник поміняє знак.
4). Спільний множник, що міститься в усіх елементах одного рядка ( стовпця ), можна винести за знак визначника
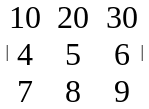 =
10·
=
10·
5). Якщо кожен елемент рядка ( стовпця ) є сумою двох доданків, то такий визначник дорівнює сумі двох визначників
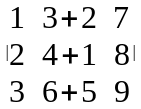 =
=
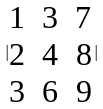 +
+
 .
.
Визначення.
Мінором
 елемента
елемента
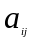 визначника
називається визначник, який утворюється
з даного визначника в результаті
викреслення
i
− го
рядка та
j
− го
стовпця
визначника
називається визначник, який утворюється
з даного визначника в результаті
викреслення
i
− го
рядка та
j
− го
стовпця
Δ
=
;
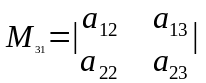 .
.
Визначення.
Алгебраїчним доповненням
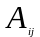 елемента
називається
його мінор, взятий зі
знаком
( −1 )
елемента
називається
його мінор, взятий зі
знаком
( −1 )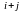 ∙
.
∙
.
Приклад.
Обчислити
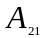 :
:
Δ
=
 ,
= ( −1 )
,
= ( −1 )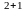 ·
·
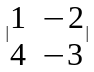 = ( −1 )
= ( −1 )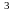 ∙ ( −3 − ( −8 )) = −1 · 5 = −5.
∙ ( −3 − ( −8 )) = −1 · 5 = −5.
Теорема 1. Визначник дорівнює сумі добутків елементів якого – небудь рядка
( стовпця ) на їхні алгебраїчні доповнення
Δ
=
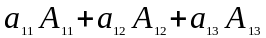 ,
або Δ =
,
або Δ =
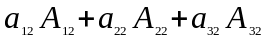 .
.
Теорема 2. Сума добутків елементів будь – якого рядка ( стовпця ) визначника на алгебраїчні доповнення відповідних елементів іншого рядка ( стовпця ) дорівнює нулю
Δ
=
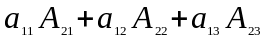 = 0.
= 0.
Теорема один дає змогу обчислити визначник п − го порядку, але такий спосіб для визначників 5 − го, 6 − го і т.п. порядків громіздкий. Тому перш ніж застосо-вувати теорему один визначник спрощують таким чином, щоб в рядку ( стовпці ) всі елементи крім одного дорівнювали нулю ( використовуючи властивість ).
Приклад.
Обчислити:
Δ
=
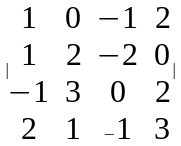 =
=
 = 1∙ ( −1 )
= 1∙ ( −1 )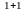 ∙
∙
 = 2 − 6 − 4 − ( 2 + 8 +
3
) = −8
− 13 = −21.
= 2 − 6 − 4 − ( 2 + 8 +
3
) = −8
− 13 = −21.
Пояснення:
Отримаємо
в першому рядку нулі, крім
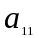 :
:
1). додамо перший стовпчик до третього стовпчика;
2). перший стовпчик помножимо на −2 і додамо до четвертого стовпчика;
3). використаємо теореми один та два.
2.Матриці.Дії над матрицями.
Означення. Матрицею розміру m x n називається прямокутна таблиця чисел, розташованих в m рядках та n стовпцях:

 α11
α12
... α1n
α11
α12
... α1n
α21 α22 ... α2n ___ ___
А=
... ... ... ...
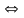 А= ( αi
j ), i = 1, m, j = 1, n
А= ( αi
j ), i = 1, m, j = 1, n
αm1 αm2 ... αmn
Якщо m = n, то матриця А називається квадратною матрицею m-го порядку, якщо m n, матриця А називається прямокутною.
Перелічимо деякі спеціальні види матриць:
1.Матриця-рядок – прямокутна матриця розміру 1х n:
А = ( α11 α12... α1n )
2. Матриця-стовпець – прямокутна матриця розміру m х 1:

α11
α12
А = ...
αm1
3. Нульова матриця − матриця, всі елементи якої дорівнюють нулю. Вона позначається символом О.
4. Діагональна матриця − квадратна матриця, у якої всі елементи з нерівними індексами ( i j ) дорівнюють нулю:
 α11
0
... 0
α11
0
... 0
0 α22 ... 0
А = ... ... ... ...
0 0 0 αm n
Кажуть, що елементи α11, α22, ..., αn n розташовані на головній діагоналі.
Діагональна матриця, у якої всі діагональні елементи рівні між собою, називається скалярною матрицею. Скалярна матриця у якої діагональні елементи дорівнюють одиниці, називається одиничною матрицею і позначається сим-волом Е.
Кожній квадратній матриці можна поставити у відповідність певне число – її визначник, або детермінант, який позначається символом det A і обчислюється за властивістю :
det
A
=
 ik
Ai
k
=
k
j
Ak
j
ik
Ai
k
=
k
j
Ak
j
Очевидно, що det О = 0, det E = 1.
Означення. Якщо визначник матриці А дорівнює нулю ( det A = 0 ), то матриця А називається особливою ( виродженою або сингулярною ), в іншому випадку (det A 0) вона називається неособливою (не виродженою).
Означення.
Якщо
в матриці А
поміняти місцями відповідні рядки
і стовпці, то отримана матриця
називається транспонованою
відповідно матриці А
і позначається
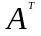 :
:
= ( αj i)
Очевидно, що det = det A ( властивість визначників ).
Операції над матрицями та властивості цих операцій.
Означення. Дві матриці А = (αi j) та В = (bi j) називається рівними ( А = В ), якщо їх розміри однакові і всі їх елементи рівні між собою, тобто для всіх і
та j αij = bi j.
Означення. Сумою двох матриць А і В однакових розмірів називається матриця С такого ж розміру (С = А + В), елементи якої дорівнюють сумі відповідних елементів матриць А та В, тобто сi j = αi j + bi j для всіх i та j.
Властивості операцій додавання матриць:
1. переставна: А + В = В + А;
2. сполучна: А + (В + С) = (А + В) + С.
Означення. Добутком матриці А на число називається матриця В ( В = А ), елементи якої дорівнюють добутку відповідних елементів матриці А на число , тобто bi j = αi j для всіх і та j.
Властивості операції множення матриці на число:
1. сполучна: ( А ) = ( )А;
2. розподільні: ( + )А = А + А,
(А
+ В) = А
+ В.

Зауваження. Матрицю А помножити на матрицю В можна тільки тоді, коли кількість стовпців матриці А дорівнює кількості рядків матриці В, такі матриці називаються узгодженими.
Означення. Добутком матриці А розміру mxp на матрицю В розміру pxn називається матриця С розміру mxn, елементи сi j якої для всіх і та j дорівнюють
сi
j
=
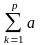 i
k
bk
j
i
k
bk
j
Властивості операції множення матриць не підкоряється переставному закону: АВ ВА.
Означення. Якщо А – квадратна матриця, а n – натуральне число, то n-ним степенем матриці А називається добуток
Аⁿ = А А ... А
n – множників
Наприклад,
А² = А А, А³ = А А² = А² А
Матриця А² називається квадратом матриці А, матриця А³ − її кубом.
Означення. Якщо А та В – квадратні матриці однакового порядку, і АВ = ВА = Е, то матриця В називається оберненою до матриці А і позна-чається символом А־¹.
Теорема існування. Для того щоб матриця А мала обернену матрицю А־¹, необхідно і достатньо, щоб матриця А була неособливою.
Правило знаходження оберненої матриці:
1.скласти матрицю алгебраїчних доповнень елементів матриці А, тобто ( Аi j );
2. транспонувати її, отримуючи приєднану матрицю
(
Аi
j
)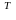 = ( A
ji
);
= ( A
ji
);
3.
помножити
приєднану
матрицю
на
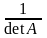 .
.
Таким чином,
А־¹ = ·(Аi j) .
В прямокутній матриці А розміру mxn можна викреслити кілька рядків і стовпців так, щоб залишені елементи утворювали квадратну матрицю порядку k ( k ≤ min ( m,n ) ). Визначник цієї матриці називається мінором матриці А.
Означення. Рангом матриці А називається найвищий порядок r відмінного від нуля її мінора.
Матриці широко використовуються в плануванні виробництва та транспорт-них перевезень. Вони дозволяють розробляти різні варіанти плана, полегшують дослідження залежності між різними економічними показниками.
Приклад.
Дано матриці А =
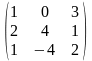 ,
В =
,
В =
 ,
С =
,
С =
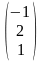 і число
= 2.
і число
= 2.
Знайти АТВ+С.
AT
=
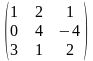 ;
ATB
=
=
;
ATB
=
=
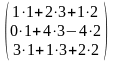 =
=
 ;
;
C
=
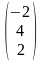 ;
АТВ+З
=
+
=
;
АТВ+З
=
+
=
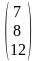 .
.
Приклад.
Знайти добуток матриць А =
 і В =
і В =
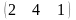 .
.
АВ
=
=
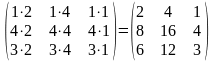 .
.
АВ = = 21 + 44 + 13 = 2 + 16 + 3 = 21.
Приклад.
Знайти добуток матриць А= , В
=
, В
=
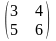
АВ
=
=
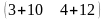 =
=
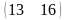 .
.
3.Обернена матриця.Способи її знаходження
Означення. Якщо А та В – квадратні матриці однакового порядку, і АВ = ВА = Е, то матриця В називається оберненою до матриці А і позна-чається символом А־¹.
Теорема існування. Для того щоб матриця А мала обернену матрицю А־¹, необхідно і достатньо, щоб матриця А була неособливою.
Правило знаходження оберненої матриці:
1.скласти матрицю алгебраїчних доповнень елементів матриці А, тобто ( Аi j );
2. транспонувати її, отримуючи приєднану матрицю
( Аi j ) = ( A ji );
3. помножити приєднану матрицю на .
Таким чином,
А־¹ = ·(Аi j) .
В прямокутній матриці А розміру mxn можна викреслити кілька рядків і стовпців так, щоб залишені елементи утворювали квадратну матрицю порядку k ( k ≤ min ( m,n ) ). Визначник цієї матриці називається мінором матриці А.
Означення. Рангом матриці А називається найвищий порядок r відмінного від нуля її мінора.
Матриці широко використовуються в плануванні виробництва та транспорт-них перевезень. Вони дозволяють розробляти різні варіанти плана, полегшують дослідження залежності між різними економічними показниками.
Приклад. Дано матриці А = , В = , С = і число = 2.
Знайти АТВ+С.
AT = ; ATB = = = ;
C = ; АТВ+З = + = .
Приклад. Знайти добуток матриць А = і В = .
АВ = = .
АВ = = 21 + 44 + 13 = 2 + 16 + 3 = 21.
Приклад. Знайти добуток матриць А= , В =
АВ = = = .
4.Формули Крамера для розв’язування систем рівнянь
При розв’язуванні рівнянь (3) можуть бути такі випадки:
1). Δ ≠ 0, тоді система (1) має єдиний розв’язок
 ;
;
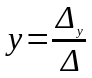 .
(3)
.
(3)
Формули (3) вперше вивів Крамер і вони називаються формулами Крамера.
2).
Δ = 0, Δ ≠
0 або Δ
≠
0 або Δ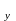 ≠
0, тоді система (1) не має розв’язків,
тобто є несумісною.
≠
0, тоді система (1) не має розв’язків,
тобто є несумісною.
3). Δ = Δ = Δ = 0, тоді система (1) зводиться до одного рівняння і має безліч розв’язків, тобто є невизначеною.
Розглянемо тепер систему трьох лінійних рівнянь з трьома невідомими x, y, z:
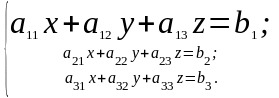 (4)
(4)
Обчислимо
визначники: Δ =
;
Δ
=
 ;
;
Δ
=
 ;
Δ
;
Δ =
=
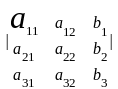 .
.
Якщо визначник систнми Δ ≠ 0, то система (4) має єдиний розв’язок, який знаходиться за формулами Крамера:
,
,
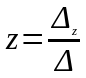 .
.
Визначення. Система лінійних рівнянь називається однорідною, якщо вільні члени в усіх рівняннях системи дорівнюють нулю, тобто система вигляду
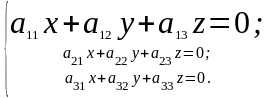
Очевидно, що така систеиа завжди має розв’язок х = 0, у = 0, z = 0, який називається нульовим. Згідно з правилом Крамера, якщо головний визначник системи Δ відміний від нуля, цей розв’язок є єдиним; якщо ж визначник системи
дорівнює нулю, то однорідна система має нескінченну кількість ненульових розвязків.
Приклад.
Розв’язати систему

=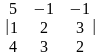 = 5(4
– 9) + (2 – 12) – (3 – 8) = −25 – 10 + 5 = −30;
= 5(4
– 9) + (2 – 12) – (3 – 8) = −25 – 10 + 5 = −30;
 =
=
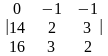 = (28
– 48) – (42 – 32) = −20 – 10 = −30;
= (28
– 48) – (42 – 32) = −20 – 10 = −30;
 ;
;
 =
=
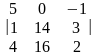 = 5(28
– 48) – (16 – 56) = −100 + 40 = −60;
= 5(28
– 48) – (16 – 56) = −100 + 40 = −60;
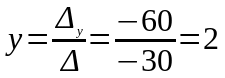 ;
;
 =
=
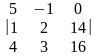 = 5(
32 – 42) + (16 – 56) = −50 – 40 = −90;
= 5(
32 – 42) + (16 – 56) = −50 – 40 = −90;
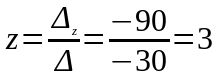 .
Відповідь:
( 1; 2; 3; ).
.
Відповідь:
( 1; 2; 3; ).
5.Матричний способ розв’язування систем рівнянь
Матричний метод роз’язання лінійних систем.
Нехай
дано систему:
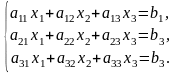
Розглянемо три матриці:

Перша
матриця називається матрицею симтеми,
друга матрицею-стовпцем змінних, третя
– матрицею-стовпцем вільних членів.
Тоді систему можна записати у матричному
вигляді:
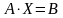 .
Якщо матриця системи рівнянь невироджена
.
Якщо матриця системи рівнянь невироджена
 ,
то розв’язок системи знаходимо у вигляді
,
то розв’язок системи знаходимо у вигляді
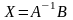 ,
або
,
або
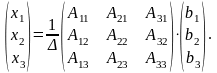
Розв’язати систему лінійних рівнянь матричним методом:

Розв’язання:
Запишемо
дану систему рівнянь у матричній формі:
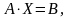 де
де

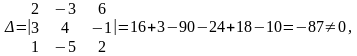 значить
матриця А
має обернену матрицю.
значить
матриця А
має обернену матрицю.
Знайдемо алгебричні доповнення елементів матриці А :
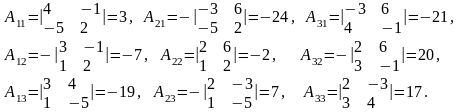

Скориставшись
рівністю
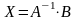 ,
знаходимо розв’язок
системи:
,
знаходимо розв’язок
системи:

 -
шуканий розв’язок.
-
шуканий розв’язок.
6.Розвязування систем рівнянь методом Гаусса
Видатний німецький математик, астроном, фізик і геодезист Карл Фрідріх Гаусс
( 30. 04. 1777 − 23. 02. 1855 ) розробив метод розв’язування таких систем лінійних алгебраїчних рівнянь. Суть метода Гаусса полягає в тому, що шляхом елементарних перетворень систему треба привести до трикутного вигляду: дана система перетворюється в рівносильну їй систему, що легко досліджується і розв’язується. Такий вигляд системи дозволяє знайти усі невідомі.
Для перетворення даної системи лінійних рівнянь загального виду до потрібного нам спеціального виду ми будемо піддавати її наступним перетворенням:
◄ додавання до обох частин одного рівняння системи відповідних частин іншого рівняння тієї ж системи, помножених на деяке число;
◄ перестановка місцями рівнянь у системі;
◄ видалення із системи рівнянь виду 0 = 0.
У результаті кожного з елементарних перетворень, а значить і в результаті послі-довного повторення їх, дана система лінійних рівнянь перетвориться в систему лінійних рівнянь, рівносильну вихідної.
Розглянемо систему лінійних рівнянь:
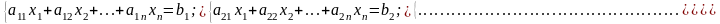
Розділемо оби дві частини першого рівняння на a11 0, потім:
1). помножимо на а21 і віднімемо від другого рівняння;
2). помножимо на а31 і віднімемо від третього рівняння;
і т.п.
Отримаємо:
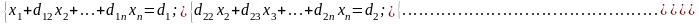 ,
де
d1j
= a1j/a11,
j
= 2, 3, …, n+1.
,
де
d1j
= a1j/a11,
j
= 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, … , n; j = 2, 3, … , n+1.
Далі повторюємо тіж самі дії для другого рівняння системи, потім для третього і тому подібне.
Приклад.
Розвязати
систему рівнянь

Щоб виключити невідому х із другого та третього рівнянь, необхідно перше рівняння системи помножити по черзі на (−3) та (−2) і додати, відповідно, до
другого та третього рівнянь. Система після першого кроку буде мати вигляд
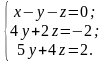
Щоб
виключити невідому у
з третього рівняння, помножимо друге
рівняння на
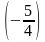 і складемо його з третім:
і складемо його з третім:
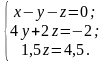
Таким
чином, після другого кроку прямий
хід закінчено. Тепер починається
зворотній хід. З третього рівня
системи знаходимо
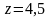 :
: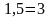 .
Це значення підставляємо до другого
рівняння і отримуємо 4у + 2 · 3 = −2,
звідки у = −2.
.
Це значення підставляємо до другого
рівняння і отримуємо 4у + 2 · 3 = −2,
звідки у = −2.
Нарешті, після підстановки значень у і z до першого рівняння, маємо х + 2 – 3 = 0, звідки знаходимо х = 1.
Відповідь: ( 1; −2; 3 ).
7.Вектор.Дії над векторами.Базисні площини в просторі
 Позначається
Позначається
 або
або
 :
А В
:
А В
(тут
точка А
–
початок , точка В – кінець вектора
).
Вектор, початок і кінець якого
збігаються, називається нульовим
вектором:
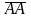 =
=
 .
Відстань між початком і кінцем
вектора називається його довжиною
і позначається:
АВ =
.
Відстань між початком і кінцем
вектора називається його довжиною
і позначається:
АВ =
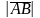 ,
а =
,
а =
 .
.
Вектори називаються колінеарними, якщо вони лежать на одній прямій або
на паралельних прямих:
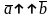 – колінеарні
і однаково напрямлені,
– колінеарні
і однаково напрямлені,
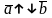 – колінеарні
і протилежно напрямлені.
– колінеарні
і протилежно напрямлені.
Два вектори називаються рівними, якщо вони колінеарні, однаково напрямлені і
мають рівні довжини. Два вектори називаються протилежними, якщо вони колі-неарні, протилежно напрямлені і мають рівні довжини.

 B
C
B
C
У
паралелограмі
АВСD
 (рівні),
(рівні),
 A
D
A
D
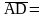 –
– (
протилежні
)
(
протилежні
)
Вектор, колінеарний даному вектору, однаково з ним напрямлений, і довжина
якого
дорівнює одиниці, називається ортом
даного вектора, Позначення:

або
 .
.
Вектори називаються компланарними, якщо вони лежать в одній площині
або в паралельних площинах.
До лінійних операцій над векторами належать операції додавання векторів
та множення вектора на число.
Додавання векторів визначається за правилом трикутника:
якщо
від кінця вектора
відкласти вектор
 ,
то їх сумою
називається вектор
,
то їх сумою
називається вектор
 (
(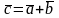 ),
що сполучає початок вектора
з кінцем вектора
.
),
що сполучає початок вектора
з кінцем вектора
.
Суму двох векторів можна також знайти за правилом паралелограма: якщо
привести вектори і до спільного початку і побудувати на них паралело-
грам, то сумою векторів і є вектор , що збігається з діагоналлю пара-
лелограма, яка виходить із спільного початку векторів і .





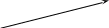

Властивості операції додавання векторів:
1.
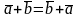 – переставна;
– переставна;
2.
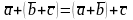 – сполучна;
– сполучна;
3.
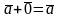
4.
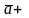 (–
) = 0.
(–
) = 0.
Різницею
векторів
і
називається
вектор
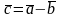 ,
який
в сумі з
вектором
дає
вектор
.
,
який
в сумі з
вектором
дає
вектор
.


Для того, щоб відняти вектор
від вектора , достатньо додати до
вектора
,
вектор (–
):
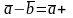 (–
).
(–
).

Визначення:
Добутком
вектора
на
число
 називається
вектор
(
називається
вектор
(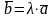 ),
який
задовольняє трьом умовам:
),
який
задовольняє трьом умовам:
1.
 ;
;
2. ;
3.
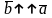 ,
якщо
0,
,
якщо
0,
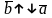 ,
якщо
0.
,
якщо
0.
Властивості операції множення вектора на число:
1.
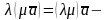 сполучна;
сполучна;
2.
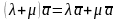 – розподільна;
– розподільна;
3.
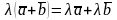 – розподільна.
– розподільна.
Справедливе твердження: вектори і колінеарні тоді і тільки тоді, коли
 .
.
Нехай
задані n
векторів
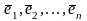 .
Тоді вираз
1
.
Тоді вираз
1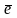 1
+
2
2
+ ... +
n
n
нази-
1
+
2
2
+ ... +
n
n
нази-
вається їх лінійною комбінацією, числа 1, 2, ... , n – коефіцієнти лінійної
комбінації. Якщо будьякий вектор представлений у вигляді лінійної комбі-
нації заданих векторів, то кажуть, що він розкладений по заданих векторах, і
коефіцієнти лінійної комбінації називаються коефіцієнтами розкладання.
Якщо існують n лінійно незалежних векторів 1, 2, ..., n, і будь-який вектор
може бути записаний у вигляді їх лінійної комбінації, то сукупність векторів
1, 2, ..., n, взятих у вказаному порядку, називається базисом. Будьякий век-
тор можна єдиним способом розкласти за векторами базиса. Коефіцієнти розкла-
дання вектора за векторами базиса називаються координатами вектора в цьо-му базисі.
Базис на площині утворюють два неколінеарні вектори, взяті у певному по-
рядку; базис у просторі утворюють три впорядковані некомпланарні вектори.
Якщо ми маємо розкладання вектора за базисними векторами:
=
 1
1
+
2
2
+
3
3,
то це записується у вигляді
(
1
,
2,
3)
або
1
1
+
2
2
+
3
3,
то це записується у вигляді
(
1
,
2,
3)
або
= ( 1 , 2, 3).
Властивості координат:
1. для рівності двох векторів необхідно і достатньо, щоб їх відповідні коорди-
нати були рівні:
=
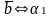 =
β1,
α2
= β2,
α3
= β3;
=
β1,
α2
= β2,
α3
= β3;
2. при додаванні двох векторів їх відповідні координати також додаються:
+ = ( α1 + β1 , α2 + β2, α3 + β3 );
3. при множенні вектора на число його координати множаться на це число:
λ = (λα1 , λα2 , λα3 )
Висновок. Якщо два вектори колінеарні, то їх координати пропорційні, і
навпаки:

Будемо
казати, що вектори
 утворюють ортогональний
базис
у
утворюють ортогональний
базис
у
просторі,
якщо вони попарно перпендикулярні:
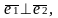
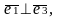
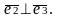
Ортогональний базис називається нормованим, якщо довжина кожного з
векторів
дорівнює одиниці:
 1.
Ми далі будемо користува-
1.
Ми далі будемо користува-
тися ортонормованим базисом, базисні вектори якого позначаються:
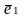 =
=
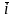 ,
,
 =
=
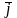 ,
,
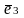 =
=
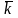 .
.
Визначення. Декартовою прямокутною системою координат називається сукупність точки і ортонормованого базису. Точка називається початком координат і позначається т. О, а числові прямі, які проходять через початок
координат у напрямку базисних ортів, називаються: х – вісь абсцис, у – вісь ординат, z – вісь аплікат.
Вектор у декартовій системі координат має координати (ах, ау, аz).
Вектор
 ,
що сполучує довільну точку М з
початком координат, нази-
,
що сполучує довільну точку М з
початком координат, нази-
вається радіусом-вектором точки М. Координатами точки М в декартовій сис-
темі координат називаються координати її радіус-вектора.
Якщо точка А(хА, уА, zА) – початок, і точка В(хВ, уВ, zВ) – кінець вектора , то його координати дорівнюють
= (хВ – хА, уВ – уА, zB – zA).
Координати
точки М, яка ділить відрізок АВ у
відношенні
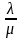 ,
то
,
то
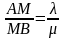 ,
можна знайти за формулами
,
можна знайти за формулами
х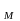 =
=
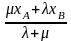 ,
у
=
,
у
=
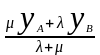 ,
z
=
,
z
=
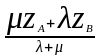
Якщо точка М є серединою відрізка АВ, то λ = μ = 1, і формули спрощуються:
хМ
=
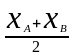 ,
уМ
=
,
уМ
=
 ,
zM
=
,
zM
=
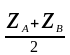
Визначення. Скалярним добутком двох векторів називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними:
 ,
,


 Властивості
скалярного добутку:
Властивості
скалярного добутку:
1.
 − переставна;
− переставна;

 2.
2.
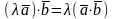 − сполучна;
φ
− сполучна;
φ
3.
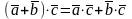 − розподільна;
− розподільна;
4.
 − скалярний
квадрат вектора дорівнює квадрату
його довжини;
− скалярний
квадрат вектора дорівнює квадрату
його довжини;
5.
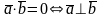 − скалярний
добуток двох ненульових векторів
дорівнює ну-
− скалярний
добуток двох ненульових векторів
дорівнює ну-
лю і тільки тоді, коли ці вектори перпендикулярні.
Якщо
вектори
і
задані декартовими координатами
 ах,
ау,
аz),
ах,
ау,
аz),
(bx, by, bz), то їх скалярний добуток можна обчислити за формулою
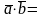 ахbx
+
ayby
+ azbz
.
ахbx
+
ayby
+ azbz
.
Застосування скалярного добутку
Обчислення довжини вектора
 ;
;
обчислення відстані між точками
АВ
=
 ;
;
Обчислення координат орта вектора
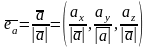 ;
;
Обчислення кута φ між двома векторами
cos
φ
=
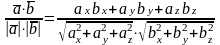 ;
;
Обчислення напрямних косинусів вектора.
Напрямні косинуси вектора – це косинуси кутів, які вектор утворює з
осями координат.
Позначимо
α
=
(
^ x
) = (
^
),
β
= (
^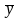 )
= (
^
),
γ
=
(
^
)
= (
^
),
γ
=
(
^
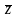 ) = (
^
),
) = (
^
),
тоді
cos
α
=
 cos
β
=
cos
β
=
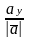 cos
γ
=
cos
γ
=
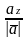 .
.
Напрямні косинуси вектора дорівнюють координатам його орта.
Перевірка перпендикулярності двох векторів
 .
.
Приклад .
Задані точки А(−1; 2; 1), В(2; 0; 2), С(1; 2; −1), D(0; 3; 1). Знайти:
координати вектора
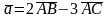 ;
;координати орта вектора ;
кут ВАС (в радіанах);
площу трикутника АВС;
5. об’єм піраміди АВСD.
Розв’язання .
Знайдемо
координати векторів
 :
:

1.
2 ·

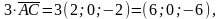
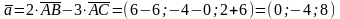
2.
Знайдемо довжину вектора
:
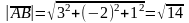 .
.


Тоді
орт вектора
дорівнює

 .
.
3. Косинус кута ВАС знайдемо за формулою
cos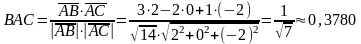
звідки
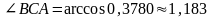 рад.
рад.
8.Скалярний,векторний та змішаний добуток векторів
Визначення. Скалярним добутком двох векторів називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними:
,
Властивості скалярного добутку:
1. − переставна;
2. − сполучна; φ
3. − розподільна;
4. − скалярний квадрат вектора дорівнює квадрату його довжини;
5. − скалярний добуток двох ненульових векторів дорівнює ну-
лю і тільки тоді, коли ці вектори перпендикулярні.
Якщо вектори і задані декартовими координатами ах, ау, аz),
(bx, by, bz), то їх скалярний добуток можна обчислити за формулою
ахbx + ayby + azbz .
Застосування скалярного добутку
Обчислення довжини вектора ;
обчислення відстані між точками
АВ = ;
Обчислення координат орта вектора
;
Обчислення кута φ між двома векторами
cos φ = ;
Обчислення напрямних косинусів вектора.
Напрямні косинуси вектора – це косинуси кутів, які вектор утворює з
осями координат.
Позначимо
α = ( ^ x ) = ( ^ ), β = ( ^ ) = ( ^ ), γ = ( ^ ) = ( ^ ),
тоді
cos α = cos β = cos γ = .
Напрямні косинуси вектора дорівнюють координатам його орта.
Перевірка перпендикулярності двох векторів
.
Приклад .
Задані точки А(−1; 2; 1), В(2; 0; 2), С(1; 2; −1), D(0; 3; 1). Знайти:
координати вектора ;
координати орта вектора ;
кут ВАС (в радіанах);
площу трикутника АВС;
5. об’єм піраміди АВСD.
Розв’язання .
Знайдемо координати векторів :
1. 2 ·
2. Знайдемо довжину вектора : .
Тоді орт вектора дорівнює .
3. Косинус кута ВАС знайдемо за формулою
cos
звідки рад.
8.скалярний,векторний та змішаний добутки
Скалярним добутком двох векторів називається число, яке дорівнює добутку довжин цих векторів на косинус кута між ними:
,
Властивості скалярного добутку:
1. − переставна;
2. − сполучна; φ
3. − розподільна;
4. − скалярний квадрат вектора дорівнює квадрату його довжини;
5. − скалярний добуток двох ненульових векторів дорівнює ну-
лю і тільки тоді, коли ці вектори перпендикулярні.
Якщо вектори і задані декартовими координатами ах, ау, аz),
(bx, by, bz), то їх скалярний добуток можна обчислити за формулою
ахbx + ayby + azbz .
Застосування скалярного добутку
Обчислення довжини вектора ;
обчислення відстані між точками
АВ = ;
Обчислення координат орта вектора
;
Обчислення кута φ між двома векторами
cos φ = ;
Обчислення напрямних косинусів вектора.
Напрямні косинуси вектора – це косинуси кутів, які вектор утворює з
осями координат.
Позначимо
α = ( ^ x ) = ( ^ ), β = ( ^ ) = ( ^ ), γ = ( ^ ) = ( ^ ),
тоді
cos α = cos β = cos γ = .
Напрямні косинуси вектора дорівнюють координатам його орта.
Перевірка перпендикулярності двох векторів
.
Приклад .
Задані точки А(−1; 2; 1), В(2; 0; 2), С(1; 2; −1), D(0; 3; 1). Знайти:
координати вектора ;
координати орта вектора ;
кут ВАС (в радіанах);
площу трикутника АВС;
5. об’єм піраміди АВСD.
Розв’язання .
Знайдемо координати векторів :
1. 2 ·
2. Знайдемо довжину вектора : .
Тоді орт вектора дорівнює .
3. Косинус кута ВАС знайдемо за формулою
cos
звідки рад.
Векторним добутком двох векторів і називається третій вектор
 ,
який задовольняє умові:
,
який задовольняє умові:
 ;
;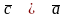 ,
,
 ;
;
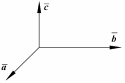
Рис. 4.1
 утворюють
праву трійку векторів, тобто третій
вектор має такий напрям, що при
спостереженні з його кінця найближчий
поворот від вектора
до
виконується
проти годинникової стрілки.
утворюють
праву трійку векторів, тобто третій
вектор має такий напрям, що при
спостереженні з його кінця найближчий
поворот від вектора
до
виконується
проти годинникової стрілки.
Векторний
добуток позначається символом
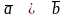 .
За визначенням випливає, що
.
За визначенням випливає, що
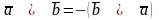 .
.
Модуль векторного добутку дорівнює площі паралелограма, побудованого на і :
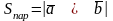 .
.
Площа трикутника обчислюється за формулою:
 .
.
Векторній добуток векторів, які задані своїми координатами, обчислюються за формулою:
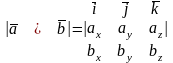 .
.
Умова колінеарності двох векторів і має вигляд:
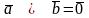 (або
(або
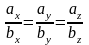 ).
).
Векторні добутки ортів дорівнюють:
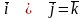 ;
; 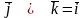 ;
;  ;
;
 ;
; 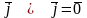 ;
; 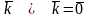 .
.
Мішаним добутком трьох векторів називається добуток
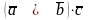 .
.
Частіше
мішаний добуток позначається
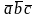 .
.
Якщо вектори задані своїми координатами, то мішаний добуток знаходять за формулою:
 .
.
Об’єм паралелепіпеду, який побудований на векторах , , як на сторонах, дорівнює модулю мішаного добутку цих векторів:
 .
.
Для об’єму піраміди маємо наступну формулу:
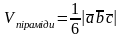 .
.
Умова
компланарності трьох векторів має
вигляд:
 .
.
Зразки розв’язування задач.
Задача
1.
Знайти скалярний добуток векторів
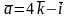 ,
,
 .
.
Розв’язання.
Знайдемо координати векторів:
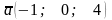 ,
,
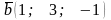 .
Тоді скалярний добуток дорівнює
.
Тоді скалярний добуток дорівнює
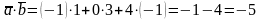 .
.
Задача
2.
Знайти кут між діагоналями паралелограма,
який побудований на векторах
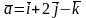 ,
,
 .
.
Розв’язання.
Як відомо, діагоналі паралелограма є
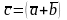 та
та
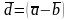 .
Знайдемо ці вектори:
.
Знайдемо ці вектори:
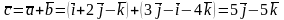 ;
;
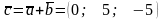 ;
;
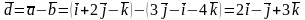 ;
;
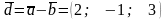 .
.
Тоді косинус кута між діагоналями знаходиться за формулою:
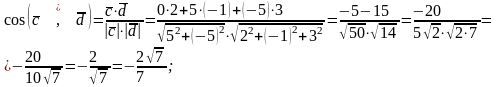
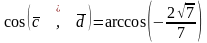 .
.
Задача
3.
Задано вектори
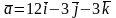 ,
,
 ,
,
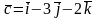 .
Обчислити проекцію вектора
.
Обчислити проекцію вектора
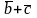 на вектор
.
на вектор
.
Розв’язання.
Знайдемо координати векторів
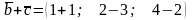 ;
;
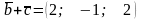 та
та
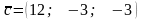 .
.
Обчислимо
проекцію
 на вектор
за формулою:
на вектор
за формулою:
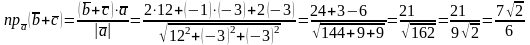 .
.
Задача
4.
Дано трикутник своїми вершинами:
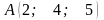 ,
,
 ,
,
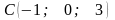 .
Покажіть, що
.
Покажіть, що
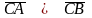 .
.
Розв’язання. Знайдемо координати векторів:
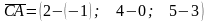 ;
;
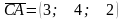 ;
;
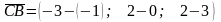 ;
;
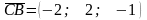 .
.
Умова
перпендикулярності двох векторів має
вигляд:
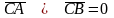 .
Перевіримо виконання цієї умови:
.
Перевіримо виконання цієї умови:
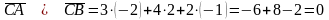 .
.
Доведено, що вектори перпендикулярні.
Задача
5.
Знайти площу паралелограма, який
побудований на векторах
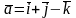 ,
,
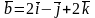 .
.
Розв’язання. Модуль векторного добутку двох векторів дорівнює площі паралелограма, який побудований на цих векторах. Знайдемо векторний добуток:

Площа паралелограма дорівнює:
 .
.
Задача
6.
Знайти площу трикутника за координатами
його вершин:
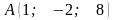 ,
,
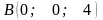 ,
,
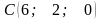 .
.
Розв’язання.
Розглянемо два вектори, на яких побудовано
трикутник, наприклад,
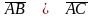 .
.
 ,
,
 .
.
Векторний добуток дорівнює:

Тоді площа трикутника дорівнює:
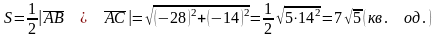 .
.
Задача 7. Розкрити дужки та спростити вираз:
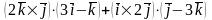 .
.
Розв’язання.
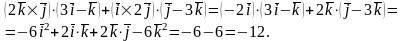
Задача
8.
При яких значеннях α
і β
вектори
 ,
,
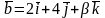 колінеарні?
колінеарні?
Розв’язання. Умова колінеарності двох векторів має вигляд:
; 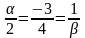 .
.
Звідки
 ;
;
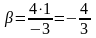 .
.
Задача
9.
Обчислити об’єм паралелепіпеду і
піраміди, які побудовані на векторах
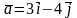 ,
,
 ,
,
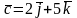 .
.
Розв’язання. Об’єм паралелепіпеду дорівнює модулю мішаного добутку векторів , , :
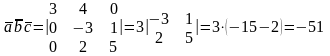 .
.
Тоді об’єми паралелепіпеду і піраміди дорівнюють:
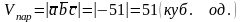 ;
;
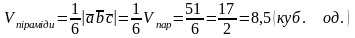 .
.
Задача
10.
Довести, що точки
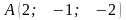 ,
,
 ,
,
 ,
,
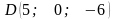 лежать в одній площині.
лежать в одній площині.
Розв’язання.
Щоб довести, що ці чотири точки лежать
в одній площині, доведемо, що в одній
площині лежать вектори
,
 ,
,
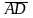 ,
тобто ці три вектори компланарні.
,
тобто ці три вектори компланарні.
Умова компланарності трьох векторів має вигляд:
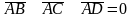 .
.
Знайдемо координати векторів:
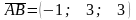 ;
;
 ;
;
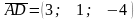 .
.
Обчислимо мішаний добуток векторів:
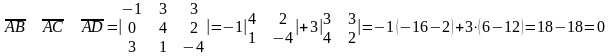 .
.
Таким чином, точки A, B, C, D лежать в одній площині.
9.Кут між векторами.Умови колінеарності та компланарності векторів
Кутом між двома векторами, відкладеними від однієї точки, називається найкоротший кут, на який потрібно повернути один з векторів навколо свого початку до положення співнаправленості з іншим вектором.
Косинус кута між векторами дорівнює скалярному добутку векторів, поділеному на добуток модулів векторів.
Формула обрахунку кута між векторами
cos α = a·b/|a|·|b|
Два вектори називаються колінеа́рними, якщо вони лежать на паралельних прямих або на одній прямій. Колінеарні вектори можуть бути співнаправленими чи протилежно направленими («антиколінеарними»).
Позначення
Колінеарні
вектори:![]()
Співнаправлені
вектори:
![]()
Протилежно
направлені вектори:
![]()
Властивості:
Якщо
![]() — вектори простору
— вектори простору
![]() . Тоді справджується:
. Тоді справджується:
Колінеарність — відношення еквівалентності.
Нульовий
вектор колінеарний довільному вектору:
![]()
Скалярний
добуток колінеарних векторів
![]() дорівнює добутку довжин векторів
(взятих зі знаком «—», якщо вектори
антиколінеарні)
дорівнює добутку довжин векторів
(взятих зі знаком «—», якщо вектори
антиколінеарні)
Критерій
колінеарності двох векторів: векторний
добуток колінеарних векторів .![]()
Критерій колінеарності двох векторів: колінеарні вектори є лінійно залежними.
На
площині 2 неколінеарних вектори
![]() утворюють базис. Це означає, що довільний
вектор
утворюють базис. Це означає, що довільний
вектор
![]() можна представити у вигляді:
можна представити у вигляді:![]() . Тоді
. Тоді
![]() будуть координатами
в даному базисі.
будуть координатами
в даному базисі.
Три вектори називаються компланарними, якщо вони лежать на паралельних площинах чи в одній площині. Компланарність — тернарне математичне відношення.
Властивості
Якщо
![]() — вектори простору
. Тоді справедливі твердження:
— вектори простору
. Тоді справедливі твердження:
Мішаний
добуток компланарних векторів
![]() . Це критерій компланарності трьох
векторів.
. Це критерій компланарності трьох
векторів.
Компланарні
вектори - лінійно залежні. Існують дійсні
числа
![]() такі, що
такі, що
![]() для компланарних
, за виключенням
для компланарних
, за виключенням
![]() чи
чи
![]() . Це критерій компланарності векторів.
. Це критерій компланарності векторів.
В
3-мірному просторі 3 некомпланарних
вектори
утворюють базис. Довільний вектор
![]() можна
представити у вигляді:
можна
представити у вигляді:
![]() . Тоді
. Тоді
![]() будуть координатами
в даному базисі.
будуть координатами
в даному базисі.
Іноді компланарними називають ті точки (або інші об'єкти), які лежать на (належать) однієї площині. 3 точки визначають площину і, тим самим, завжди (тривіально) компланарність. 4 точки, в загальному випадку (в загальному положенні), не компланарні.
10.Рівняння прямої на площині з направляючим вектором
РІВНЯННЯ ПРЯМОЇ ЧЕРЕЗ СПРЯМОВУЮЧИЙ ВЕКТОР.
Нехай
пряма лінія проходить через т. Мо(хо,
yo)
і паралельна вектору
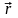 =
(m,n). Тоді її рівняння може мати вигляд
=
(m,n). Тоді її рівняння може мати вигляд
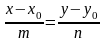 (4.7)
(4.7)


 M1
(l1)
M1
(l1)
h

 M2
(l2)
M2
(l2)
Рис. 4.1.
Вектор називається спрямовуючим вектором. Якщо є дві прямі
 (l1)
(l1)
 (l2)
(l2)
то якщо
а)
(l1)
(l2)
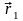 = (m1,n1)
= (m1,n1)
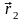 = (m2,n2)
(
,
)
= 0
= (m2,n2)
(
,
)
= 0
m1m2 + n1n2 = 0 (4.8)
б)
(l1)
|| (l2)
||
 (4.9)
(4.9)
в)
cosφ
=
 (4.10)
(4.10)
Приклад 4.6. Знайти рівняння прямої, що проходить через т. М(2,3) і паралельна прямій х + 3у - 1 = 0.
Розв'язок. Рівняння заданої прямої можна переписати у вигляді
 .
.
Звідси = (3,-1). Рівняння шуканої прямої можна записати у такому ж вигляді, враховуючи, що може виступити і в якості її спрямовуючого вектора. Тоді це рівняння має вигляд

x
+ 3y
– 11 = 0.
x
+ 3y
– 11 = 0.
Приклад 4.7. Нехай є дві паралельні прямі (l1) та (l2). Знайти відстань h між ними.
Розв'язок. Точки M1(x1,y1) та М2(х2,у2) лежать на прямих (l1) та (l2) відповідно.
Віднесемо
початок
вектора
в
точку
М2.
Вектор
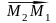 = (х1
- x2,
у1
- у2).
Побудуємо
на векторах
та
, як на сторонах паралелограм. Тоді площа
S цього паралелограму може бути обчислена
за двома формулами:
= (х1
- x2,
у1
- у2).
Побудуємо
на векторах
та
, як на сторонах паралелограм. Тоді площа
S цього паралелограму може бути обчислена
за двома формулами:
S
= |[
,
]|;
S = h · |
|
h =
 (4.11)
(4.11)
Приклад 4.8. Нехай є дві прямі: 3x + 2у - 1 = 0 (l1); 6х + 4у + 1 = 0 (l2). Знайти відстань між цими прямими .
Розв’язок. Очевидно, що прямі (l1) та (l2) - колінеарні. Перепишемо обидва рівняння у вигляді
3x
+ 2у - 1 = 0
3х = -2( у
-
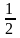 )
)
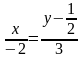 (l1)
(l1)
6х
+ 4у + 1 = 0
6х = -4(у
+
 )
)
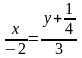 (l2)
(l2)
З отриманих формул витікає, що т. М1(0, ), т. М2(0, - ) належать (l1) та (l2) відповідно, а вектор = (-2, 3) - спрямовуючий вектор цих паралельних прямих. Скористаємось формулою (4.11), для чого обчислимо вектор та [ , ]:
=
(0, )
,
)
,
[
,
]
=
 = (0, 0,
= (0, 0,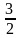 ),
),
|[ , ]| = ,
|
|
=
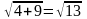 ,
,
h
=
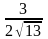 .
.
Приклад 4.9. Знайти рівняння бісектриси кута при вершині В трикутника АВС, якщо координати його вершин відомі: A(-1, 2), B(3, 0), C(1,4).
Розв'язок.
Скористаємось рівнянням прямої через
спрямовуючий вектор (4.7). Спрямовуючим
вектором бісектриси може бути вектор,
що співпадає з вектором-діагоналлю
ромба, сторони якого мають той же напрям,
що і вектори ВА° та BС°
- орт-вектори векторів
 та
та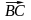 .
Сама діагональ матиме напрям
вектора
°
+
°.
.
Сама діагональ матиме напрям
вектора
°
+
°.
=
(-4,2)
°
= (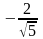 ,
,
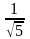 )
= (
)
= ( ,
,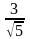 )
=
(-1,1).
)
=
(-1,1).
=
(-2,4)
°
= (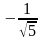 ,
,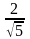 )
)
Рівняння бісектриси має вигляд: х - 3 = - у х + у - 3 = 0.
Приклад 4.10. Знайти відстань h від точки M(-1, 1) до прямої 3x + 5у- 1 = 0.
Розв'язок. Перепишемо рівняння заданої прямої у вигляді (4.7).
3х
+ 5у –1 = 0
 ,
,
т.
М1(0,
 )
належить цій прямій, і спрямовуючий
вектор
=
(-5, 3).
)
належить цій прямій, і спрямовуючий
вектор
=
(-5, 3).
 =(-1,
=(-1,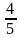 ).
Побудуємо паралелограм на векторах
та
,
як на сторонах. Тоді має місце формула
).
Побудуємо паралелограм на векторах
та
,
як на сторонах. Тоді має місце формула
h
=
 ,
,
[
,
]
=
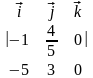 = (0,0,1),
= (0,0,1),
[
,
]
= 1
h
=
 .
.
11.Рівняння прямої на площині із нормальним вектором.Загальне рівняння прямої,його дослідження
НОРМАЛЬНЕ РІВНЯННЯ ПРЯМОЇ.
Якщо пряму задати за допомогою кута α, що утворює її нормальний вектор, проведений з початку координат до прямої, з додатнім напрямком осі ОХ, і відстані прямої від початку координат р (Рис. 4.2), то її рівняння матиме вигляд
x cosα + y sinα – p = 0 (4.17)
 y
y
 (l)
(l)

 p
p

 O
α
x
O
α
x
Рис. 4.2.
Цей
тип рівняння прямої має назву "нормальне
рівняння прямої".
Якщо пряму задано в загальному вигляді
Ах + Ву + С = 0, її можна привести до
нормального вигляду, якщо домножити
ліву і праву частини цього рівняння на
множник ± .
Знак y множника повинен бути протилежним
знакові вільного члена С.
.
Знак y множника повинен бути протилежним
знакові вільного члена С.
Примітка. cоsα , sinα - це координати орт-вектора нормального вектора прямої, напрямленого від початку координат до прямої. Якщо в загальному рівнянні вільний член С має від'ємний знак, то нормальний вектор = (А,В} має саме такий напрям, в протилежному випадку такий напрям має нормальний вектор = (-А, -В).
ЗАГАЛЬНЕ РІВНЯННЯ ПРЯМОЇ.
Означення 4.1. Рівняння
Ах + Ву + С = 0 (4.1)
називається загальним рівнянням прямої лінії на площині в декартовій прямокутній системі координат.
Вектор
 =(А,
В) називається нормальним
вектором прямої,
якщо він ортогональний до прямої.
=(А,
В) називається нормальним
вектором прямої,
якщо він ортогональний до прямої.
Рівняння вигляду
А(х – хо) + В(у - уо) = 0 (4.2)
є рівнянням прямої лінії, що ортогональна вектору-нормалі = (А, В) і проходить через т. Мо(хо, уо).
Якщо є дві прямі лінії
A1x + B1y + C1 = 0 (l1)
A2x + B2y + C2 = 0 (l2)
то якщо:
a)
(l1)
(l2)
 = ( А1,
В1)
,
= ( А1,
В1)
,
 =
( А2,
В2)
=
( А2,
В2)
( , ) = 0 А1А2 + В1В2 = 0 (4.3)
б)
(l1)
|| (l2)
||
 (4.4)
(4.4)
в)
cosφ
=
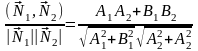 (4.5)
(4.5)
де - один з кутів між прямими (l1) та (l2).
Приклад
4.1.
Знайти рівняння прямої
лінії,
що проходить через т. М{-2,1)
і
ортогональна вектору
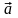 = (-1, 2).
= (-1, 2).
Розв'язок. Очевидно, що вектор можна використати в якості вектора-нормалі. Тоді, скориставшись рівнянням прямої типу (4.2), отримаємо:
-(х + 2) + 2(у - 1) = 0 -х + 2у - 4 = 0.
Шукане рівняння має вигляд: х - 2у + 4 = 0.
Приклад 4.2. Знайти рівняння прямої, що проходить через т. М(-7,3) і паралельна прямій 3х - у + 1 = 0.
Розв'язок. Вектор-нормаль заданої прямої = (3, -1) можна використати в якості вектора до шуканої прямої. Тому рівнянням, що нас цікавить буде:
3(х + 7) - (у - 3) = 0 3х - у + 24 = 0.
Приклад. 4.3. Знайти рівняння прямої, що ортогональна прямій і проходить через точку М(-1, 1).
Розв'язок. Будемо шукати рівняння типу (4.2): А(х + 1) + В(у - 1) = 0. Параметри А та В знайдемо з умови ортогональності двох прямих (4.4). Тоді

А
= -В
-В(х – 1) + В(у – 1) = 0
х – у =2.
А
= -В
-В(х – 1) + В(у – 1) = 0
х – у =2.
Приклад 4.4. Знайти кут між двома прямими х + у + 1 = 0 та -х + у + 2 = 0.
Розв’язок. Обчислимо косинус кута між заданими прямими за формулою (4.5).
= (1,1); =(-2,1);
(
,
)
= -2 + 1 = -1; |
|
=
 ;
|
|
=
;
|
|
=
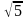 ;
;
cos
=
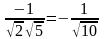 .
.
12.Рівняння прямої на площині,яка проходить через задані дві точки.Рівняння прямої у відрізках на осях
РІВНЯННЯ ПРЯМОЇ, ЩО ПРОХОДИТЬ ЧЕРЕЗ ДВІ ТОЧКИ.
Нехай
пряма проходить через дві точки М1(x1,у2)
та M2(x2,y2)
точка
М(x,
у)
-
її довільна точка. Тоді вектор
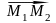 = (x2
-
x1,y2
-
y1)
може виступати в якості спрямовуючого
вектора цієї прямої. Використовуючи
рівняння прямої через спрямовуючий
вектор (4.7), отримаємо рівняння
= (x2
-
x1,y2
-
y1)
може виступати в якості спрямовуючого
вектора цієї прямої. Використовуючи
рівняння прямої через спрямовуючий
вектор (4.7), отримаємо рівняння
 (4.13)
(4.13)
Приклад 4.12. Знайти рівняння медіани, проведеної з вершини А трикутника АВС якщо його вершини А(-1, 2), В(3,2), С(1, 4),
Розв'язок.
Медіана, що проходить через вершину А,
повинна проходити через середину сторони
ВС. Користуючись формулами ділення
відрізку в заданому відношенні, знайдемо
координати середини ВС: х =
 =
2, у =
=
2, у =
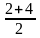 = 3. Тоді рівняння шуканої медіани буде
мати вигляд
= 3. Тоді рівняння шуканої медіани буде
мати вигляд
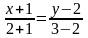
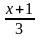 =
y
- 2
x
- 3y
+ 7 = 0.
=
y
- 2
x
- 3y
+ 7 = 0.
Рівняння прямої в відрізках на осях
Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках:
x/a + y/b = 1
13.Рівняння прямої з кутовим коефіцієнтом.Умова паралельності і перпендикулярності двох прямих
Кутовий коефіцієнт у рівнянні прямої
Якщо рівняння прямої можна записати у вигляді, то коефіцієнт k називається кутовим коефіцієнтом прямої.
1. Дві прямі паралельні тоді й тільки тоді, коли у них збігаються кутові коефіцієнти, а точки перетину з віссю ординат різні.
2. Кутовий коефіцієнт з точністю до знака дорівнює тангенсу гострого кута, утвореного прямою з віссю абсцис (або дорівнює тангенсу кута між прямою й додатним напрямком осі Ox).
3. Прямі, що задані рівняннями і, перпендикулярні тоді й тільки тоді, коли .
РІВНЯННЯ ПРЯМОЇ ЧЕРЕЗ КУТОВИЙ КОЕФІЦІЄНТ.
Означення 4.2. Рівняння вигляду
y - yo = k(x-xo) (4.14)
називається "рівнянням прямої через кутовий коефіцієнт", точка Mo(xo,yo) належить цій прямій, а параметр k - тангенс кута нахилу прямої до додатнього напряму осі ОХ має назву "кутовий коефіцієнт".
Якщо є рівняння двох прямих
y – y1 = k(x-x1) (l1),
y – y2 = k(x-x2) (l2),
то якщо
а)
(l1)
(l2)
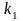 =
=
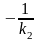 (4.15)
(4.15)
б) (l1) || (l2) k1 = k2 (4.16)
в)
tgφ
=

де φ – кут між прямими (l1) та (l2) .
Приклад 4.13. Знайти рівняння висоти трикутника, що виходить з вершини А, якщо рівняння його сторін
AB:
y = 2x + 1, BC: y =
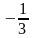 x
+
x
+
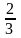 ,
AC: y = - x – 3.
,
AC: y = - x – 3.
Розв'язок. Знайдемо координати точки А, що є точкою перетину прямих АВ та АС

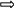 y
= 2x + 1 2x + 1 = -x –3 x =
y
= 2x + 1 2x + 1 = -x –3 x =

y
= - x – 3 y = 2x + 1 y =
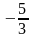
Висота, що виходить з вершини А ортогональна до сторони ВС і тому кутовий коефіцієнт рівняння цієї висоти дорівнює 3. Таким чином, рівняння шуканої висоти має вигляд
y
+ 3
=
3(x +
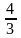 )
y
= 3х
+
)
y
= 3х
+
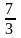 .
.
Приклад 4.14. Чи буде трикутник, рівняння сторін якого у = х +1, у = -х + 1, у = 2х + 3, прямокутним?
Розв'язок. Очевидно, що рівняння у = х + 1 та у = - х + 1 є рівняннями ортогональних сторін, тобто трикутник прямокутний.
Приклад 4.15. Знайти рівняння прямої, що проходить через початок координат і паралельна прямій у = 5х – 1.
Розв'язок. Очевидно, що кутовий коефіцієнт заданої прямої k = 5. Шукана пряма їй паралельна і тому в неї той же кутовий коефіцієнт. Використовуючи рівняння прямої через кутовий коефіцієнт (4.14) отримаємо рівняння шуканої прямої у = 5x .
Умова
паралельності двох прямих у просторі
має вигляд: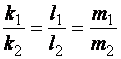
а
умова перпендикулярності двох прямих
у просторі:![]()
Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються. В деяких шкільних означеннях, щоправда, паралельні прямі не можуть збігатись, але тут цей факт не береться до уваги.
[ред.]
Властивості
Паралельність — Бінарне відношення еквівалентності, тому разбиває всю множину прямих на класи паралельних між собою.
Через довільну точку можна провести лише одну пряму, паралельную даній. Це властивість евклідової геометрії, в інших геометріях число 1 замінено іншими (в геометрії Лобачевского таких прямих минімум дві).
Дві паралельні прямі в просторі лежать в одній площині.
При перетині двох паралельних прямих третьою, т. зв. січною:
Січна обов'язково перетинає обидві прямі.
При перетині утворюється 8 кутів, при чому деякі характерні їх пари мають особливі назви та властивості:
Перехресні кути рівні.
Відповідні кути рівні.
Односторонні кути в сумі становлять 180°.
І, очевидно, суміжні кути в сумі становлять 180°, а вертикальні — рівні.
Дві прямі на площині називаються перпендикулярними, якщо при перетині вони утворють 4 прямих кути. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
В
аналітичному вигляді прямі, задані
лінійними функціями
![]() і
і
![]() будуть перпендикулярними, якщо
виконується умова
будуть перпендикулярними, якщо
виконується умова
![]() . (Тут
. (Тут
![]() —
кути нахилу прямої до горизонталі)
—
кути нахилу прямої до горизонталі)
14.Кут між прямими на площині.Умова паралельності і перпендикулярності двох прямих.Відстань від точки до прямої
Кутом між прямою та площиною називається кут між цією прямою і її проекцію (ортогональною) на площину.
Якщо пряма перпендикулярна до площини, то кут між нею й площиною вважається таким, що дорівнює , а між паралельними прямою та площиною таким, що дорівнює 90 градусів .
Кут між прямою та площиною і кут між цією прямою й перпендикуляром до площини в сумі дорівнюють 90 нрадусів.
На
рисунку
![]() .
.

Умова паралельності двох прямих у просторі має вигляд:
а умова перпендикулярності двох прямих у просторі:
Паралельними (рівнобіжними) прямими називають прямі, котрі лежать в одній площині і або збігаються, або не перетинаються. В деяких шкільних означеннях, щоправда, паралельні прямі не можуть збігатись, але тут цей факт не береться до уваги.
[ред.]
Властивості
Паралельність — Бінарне відношення еквівалентності, тому разбиває всю множину прямих на класи паралельних між собою.
Через довільну точку можна провести лише одну пряму, паралельную даній. Це властивість евклідової геометрії, в інших геометріях число 1 замінено іншими (в геометрії Лобачевского таких прямих минімум дві).
Дві паралельні прямі в просторі лежать в одній площині.
При перетині двох паралельних прямих третьою, т. зв. січною:
Січна обов'язково перетинає обидві прямі.
При перетині утворюється 8 кутів, при чому деякі характерні їх пари мають особливі назви та властивості:
Перехресні кути рівні.
Відповідні кути рівні.
Односторонні кути в сумі становлять 180°.
І, очевидно, суміжні кути в сумі становлять 180°, а вертикальні — рівні.
Дві прямі на площині називаються перпендикулярними, якщо при перетині вони утворють 4 прямих кути. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. Теорема 1. Якщо дві прямі, які перетинаються, паралельні відповідно двом іншим перпендикулярним прямим, то інші прямі теж перпендикулярні. Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих (див. рисунок). (Усі прямі лежать у площині, яка перпендикулярна до даної прямої і перетинає її у даній точці.)
В аналітичному вигляді прямі, задані лінійними функціями і будуть перпендикулярними, якщо виконується умова . (Тут — кути нахилу прямої до горизонталі)
Відстань від точки до прямої — дорівнює довжині перпендикуляра, опущеного з точки на пряму.
Якщо s = {m; n; p} - напрямний вектор прямої l, M1(x1, y1, z1) - точка що належить прямій, тоді відстань від точки M0(x0, y0, z0) до прямої l можна знайти, використовуючи формулу
d = |M0M1×s|/|s|
Вивід формули
Якщо задано рівняння прямої l то нескладно знайти s = {m; n; p} - напрямний вектор прямої і M1(x1, y1, z1) - координати точки що належить цій прямій. Із властивостей векторного добутку відомо, що модуль векторного добутку векторів дорівнює площі паралелограма побудованого на цих векторах
S = |M0M1×s|.
З іншого боку площа паралелограма дорівнює добутку його сторони на висоту проведену до цієї сторони
S = |s|d.
В нашому випадку висота буде дорівнювати відстані від точки до площини d, а сторона паралелограма дорівнює модулю напрямного вектора s.
Прирівняв площі нескладно отримати формулу відстані від точки до прямої.
15.Площина в просторі.Загальне рівняння площини та його дослідження
ЗАГАЛЬНЕ РІВНЯННЯ ПРЯМОЇ.
Означення 4.1. Рівняння
Ах + Ву + С = 0 (4.1)
називається загальним рівнянням прямої лінії на площині в декартовій прямокутній системі координат.
Вектор =(А, В) називається нормальним вектором прямої, якщо він ортогональний до прямої.
Рівняння вигляду
А(х – хо) + В(у - уо) = 0 (4.2)
є рівнянням прямої лінії, що ортогональна вектору-нормалі = (А, В) і проходить через т. Мо(хо, уо).
Якщо є дві прямі лінії
A1x + B1y + C1 = 0 (l1)
A2x + B2y + C2 = 0 (l2)
то якщо:
a) (l1) (l2) = ( А1, В1) , = ( А2, В2)
( , ) = 0 А1А2 + В1В2 = 0 (4.3)
б) (l1) || (l2) || (4.4)
в) cosφ = (4.5)
де - один з кутів між прямими (l1) та (l2).
Приклад 4.1. Знайти рівняння прямої лінії, що проходить через т. М{-2,1) і ортогональна вектору = (-1, 2).
Розв'язок. Очевидно, що вектор можна використати в якості вектора-нормалі. Тоді, скориставшись рівнянням прямої типу (4.2), отримаємо:
-(х + 2) + 2(у - 1) = 0 -х + 2у - 4 = 0.
Шукане рівняння має вигляд: х - 2у + 4 = 0.
Приклад 4.2. Знайти рівняння прямої, що проходить через т. М(-7,3) і паралельна прямій 3х - у + 1 = 0.
Розв'язок. Вектор-нормаль заданої прямої = (3, -1) можна використати в якості вектора до шуканої прямої. Тому рівнянням, що нас цікавить буде:
3(х + 7) - (у - 3) = 0 3х - у + 24 = 0.
Приклад. 4.3. Знайти рівняння прямої, що ортогональна прямій і проходить через точку М(-1, 1).
Розв'язок. Будемо шукати рівняння типу (4.2): А(х + 1) + В(у - 1) = 0. Параметри А та В знайдемо з умови ортогональності двох прямих (4.4). Тоді
А = -В -В(х – 1) + В(у – 1) = 0 х – у =2.
Приклад 4.4. Знайти кут між двома прямими х + у + 1 = 0 та -х + у + 2 = 0.
Розв’язок. Обчислимо косинус кута між заданими прямими за формулою (4.5).
= (1,1); =(-2,1);
( , ) = -2 + 1 = -1; | | = ; | | = ;
cos = .
16.Рівняння площини що проходить через три задані точки.Рівняння площини у відрізках на осях
. Рівняння площини, яка проходить через три точки
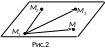 Нехай
дано три точки
Нехай
дано три точки
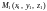 ,
,

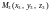 ,
які не лежать на одній прямій (рис. 2).
Ці точки однозначно визначають площину.
Знайдемо рівняння цієї площини. Для
цього візьмемо у цій площині довільну
точку
,
які не лежать на одній прямій (рис. 2).
Ці точки однозначно визначають площину.
Знайдемо рівняння цієї площини. Для
цього візьмемо у цій площині довільну
точку
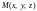 і
утворимо вектори
і
утворимо вектори
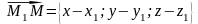 ,
,
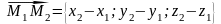

Оскільки
усі чотири точки лежать в одній площині,
а, отже, і утворені вектори, то ці вектори
компланарні. Згідно з умовою компланарності
мішаний добуток
 ,
або в координатній формі
,
або в координатній формі
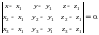 (3)
(3)
Отже, (3) – рівняння площини, що проходить через три задані точки.
Розкриваючи визначник за елементами першого рядка, одержимо загальне рівняння площини .
