38. Стохастические процессы. Особые случаи
Набор случ. эл-тов X(t), где t θсR (веществ. числа) наз. стохастическим процессом(СП).
Дискр. СП опр-тся как посл-ть случ. переменных X (t) в дискр. моменты времени t = t1, t 2, ..., tТ
Мат. ожидание E(Xt) м. изменяться во времени т.е. явл. ф-цией среднего от времени μt = E[Xt]
Также и дисперсия σt2 = E[(Xt – μt)2]
Для случ. процесса в общ. сл. в каждый момент времени опр-ная дисп. Хар-кой случ. процесса явл. автоковариация γt1,t2 =cov(Xt1, Xt2) = E[(Xt1- μt1)(Xt2- μt2)]. В общ. виде зависит от каждого t1 и t 2.
СП Xt наз. стационарным в сильном смысле, если совместное распр-ние вероятностей всех переменных Xt1, Xt2,…, Xtn то же самое, что и для переменных Xt1+τ, Xt2+τ,…, Xtn+τ. Cтац. в слабом смысле наз. СП, для кот. среднее и дисперсия независит от момента измерения, а автоковар. зависит только от длины лага между переем, т.е. μt =μ = const; σt2 = σ = const; γt1,t2= γt2–t1= γτ, где τ = t2 - t1 (лаг)
Число периодов, по кот. рассчитывается коэф. автокоррел. наз. лагом.
Автоковар. как ф-ция длины лага τ наз. автоковар. функцией, т.е. γ(τ) = γτ = E [(Xt - μ)(Xt-τ – μ)].
Для дискр. процессов поскольку t=1, 2,…,T величина лага также м.б. дискр., т.е. τ=1,2,… и τ0=σ2 . Автокорреляц ф-ция им. вид: При этом ρτ [-1;1] явл. безразм. величиной.
Замеч. 1) СП стацион. в сильн. см. всегда стацион-рен в слаб.– обр. не верно; 2) Если процесс Xt – стационарен, то его реал-ция (ВР) также стац-рна..
На практике стац-сть ВР означает отсутствие: ·тренда; ·систематич. изм. дисп; ·строго периодичных флуктуаций; ·автокорр. и автоковар. ВР.
Особые случаи
Процесс наз. нормальным, если совместное распр-ние Xt ,Xt,...,Xt это п-мерное норм. распр. В этом сл. из стационарности в слабом смысле следует стац-ть в сильном смысле.
«Белым шумом» наз. чисто случ. процесс, т.е. процесс, в кот, at явл. iid. Главные св-ва «белого шума»:
μt= E(at) = const = μ;
σt2 = const = σa;
γt1t2=0 для t1≠t2
Из этого очевидным образом => стационарность. «Белый шум» играет важную роль при модел-нии остатков или шоков стохастического процесса, генерирующего данные (ВР).
Для того чтобы проверить, является ли временной ряд хt «белым шумом», можно протестировать его выборочную автокорреляцию rх с помощью Q-статистики Бокса-Пирса.
33. Построение аддитивной модели временного ряда
Существует 2 подхода к анализу стр-ры временных рядов (ВР): 1) Классический (простейший) опр-ет тенденцию (Т), сезонную (S) и случ. (Е) компоненты методом скользящей средней; 2) С исп-нием фикт. переменных.
Все модели ВР с сез. компонентой: аддит. Y=T+S+Е и мультипл.Y=TSЕ
Выбор одной из 2-х моделей осуществляется на основе анализа структуры сез. колебаний. Если амплитуда колебаний ≈ постоянна – это аддит. модель. Если ампл. возрастает или уменьшается – это мультипл. модель.
Классич. подход сводится к расчету значений Т, S и Е для каждого уровня и процесс построения модели вкл. в себя след. шаги:
1. Выравнивание исх. ряда методом скользящей средней.
2. Расчет значений сез. компоненты S.
3. Устранение сез. компоненты из исх. ур-ней ряда и получение выравненных данных (Т + Е).
4. Аналитическое выравнивание ур-ней (Т + Е) и расчет значений Т с исп-нием полученного ур-ния тренда.
5. Расчет полученных по модели значений (Т + Е).
6. Расчет абсол. и/или относит. ошибок Е. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исх. уровни ряда и в дальнейшем исп-ть ВР ошибок Е для анализа взаимосвязи исх. ряда и др. ВР.
Построение аддитивной модели временного ряда:
Пусть ВР содержит сез. колебания с периодом 4. Строим график и определяем ≈ равную амплитуду колебаний – это опр-ет аддит. модель. Рассчитаем ее компоненты. 1-ая графа таблицы содержит № кварталов, а 2-ая – отображает значения (фактич. ур-нь ряда).
Шаг 1. Проведем выравнивание исх. уровней ряда методом скользящей средней. Для этого: a) Σ уровни ряда последовательно за каждые 4 квартала со сдвигом на один момент времени; б) разделив полученные суммы на 4, найдем скользящие средние; в) найдем ср. значения из двух последовательных скользящих средних – центрированные ск. средние.
Замеч. Полученные т.о. выровненные значения уже не содержат сез. компоненты.
Шаг 2.
Найдем оценки сез. компоненты как
разность между фактич. уровнями ряда и
центрир. ск. средними. Используем эти
оценки для расчета значений S.
Для этого найдем ср. за каждый квартал
(по всем годам) оценки сез. компоненты
.
В аддит. модели Σ значений сез. компоненты
по всем кварталам = 0. Если Σ
≠
0, вводим корректирующий
коэф. k
= Σ
/4.
Рассчитаем
скорректированные значения сез.
компоненты как разность между ее средней
оценкой и k:
,
i=(1,4)
Проверяем условие ΣSi=0. => получаем знач. сез компоненты: S1(I квартал), S2(II кв), S3(III кв), S4(IV кв). Затем вносим полученные значения сез. компоненты для каждого из кварталов.
Шаг 3. Искл-ем влияние сез. компоненты Т + Е = Y – S.
Ш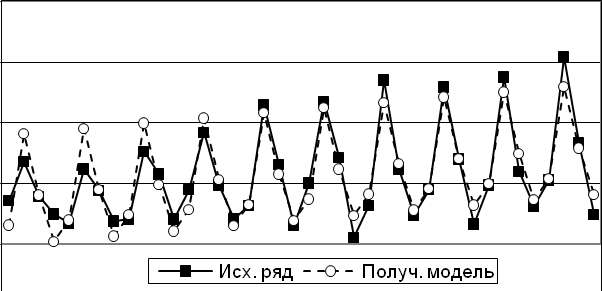
аг
4.
Определим компоненту Т
данной
модели: T
= a
+ bt,
где а – нач.
уровень ВР (t = 0);
b – ср.
за период абс. прирост уровней ряда.
Подставив значения t,
найдем уровни тенденции T
для каждого момента времени
Шаг 5. Найдем значения уровней ряда, полученные по аддит. модели: T+S.
Шаг 6. Получим абс. ошибки: E = Y – (T + S)
По аналогии с моделью регрессии для оценки качества построения модели, и для выбора наилучшей модели м. использовать ΣE2. На рис ○ – фактич, ● – теоретические значения уровней ВР
Аддит. модель объясняет Z% = 100% – ΣE2/Σ(Yi- Yср).
Прогнозирование по аддит. модели. Прогнозное значение Ft = Tt + Si. Для определения трендовой комп-ты воспользуемся ур-нием тренда T = a + bt.