Понятие числового ряда, частичная сумма ряда, сумма и остаток ряда, сходимость и расходимость ряда.

Числовой ряд – это сумма членов числовой последовательности вида

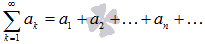
Частичная сумма числового ряда – это сумма вида , где n – некоторое натуральное число. называют также n-ой частичной суммой числового ряда.

Числовой ряд называется сходящимся, если существует конечный предел последовательности частичных сумм 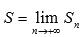. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд называется расходящимся.

Суммой сходящегося числового ряда называется предел последовательности его частичных сумм, то есть, .

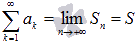Ряд, состоящий из членов геометрической прогрессии. Гармонический ряд. Основные свойства сходящихся рядов.

Сумма вида 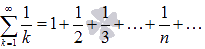называется гармоническим числовым рядом.

Свойства сходящихся числовых рядов.

1. Если сходится числовой ряд , то сходящимся будет и ряд . Другими словами, сходящимся будет и ряд без первых m членов. Если к сходящемуся числовому ряду добавить несколько членов (от первого до m-ого), то полученный ряд также будет сходящимся.

2. Если сходится числовой ряд и его сумма равна S, то сходящимся будет и ряд , причем 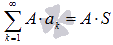, где A – произвольная постоянная.

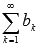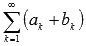3. Если сходятся числовые ряды и , их суммы равны A и B соответственно, то сходящимися будут ряды и , причем их суммы будут равны A + B и A - B соответственно.

Необходимое и достаточное условия сходимости ряда (критерий Коши).

Необходимое условие сходимости ряда.

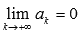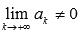Если числовой ряд сходится, то предел его k-ого члена равен нулю: . При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если , то ряд расходится. С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства не говорит о сходимости числового ряда . 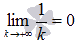К примеру, для гармонического ряда необходимое условие сходимости выполняется , а ряд расходится.

Необходимое условие сходимости ряда.

Если числовой ряд сходится, то предел его k-ого члена равен нулю: . При исследовании любого числового ряда на сходимость в первую очередь следует проверять выполнение необходимого условия сходимости. Невыполнение этого условия указывает на расходимость числового ряда, то есть, если , то ряд расходится. С другой стороны нужно понимать, что это условие не является достаточным. То есть, выполнение равенства не говорит о сходимости числового ряда . К примеру, для гармонического ряда необходимое условие сходимости выполняется , а ряд расходится.

Достаточные условия сходимости положительных рядов (признаки сравнения, признак Даламбера).

Признак Даламбера.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится. Замечание. Признак Даламбера справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится. Если , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.

Первый признак сравнения рядов. Пусть и - два знакоположительных числовых ряда и выполняется неравенство для всех k = 1, 2, 3, ... Тогда из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость . Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть , разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом , то есть, гармонический ряд. Рассмотрим несколько примеров.

Второй признак сравнения. Пусть и - знакоположительные числовые ряды. Если , то из сходимости ряда следует сходимость . Если , то из расходимости числового ряда следует расходимость . Следствие. Если и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость. Исследуем ряд на сходимость с помощью второго признака сравнения. В качестве ряда возьмем сходящийся ряд . Найдем предел отношения k-ых членов числовых рядов: 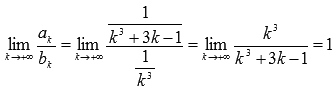Таким образом, по второму признаку сравнения из сходимости числового ряда следует сходимость исходного ряда.

Третий признак сравнения. Пусть и - знакоположительные числовые ряды. Если с некоторого номера N выполняется условие 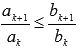, то из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .

Достаточные условия сходимости положительных рядов (признак Коши, интегральный признак Коши).

Радикальный признак Коши.

Пусть - знакоположительный числовой ряд. Если , то числовой ряд сходится, если , то ряд расходится. Замечание. Радикальный признак Коши справедлив, если предел бесконечен, то есть, если , то ряд сходится, если , то ряд расходится. Если , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение. Рассмотрим несколько примеров.