
- •4.Примеры логических ф-й.
- •5. Представления булевых функций формулами:
- •6. Представления булевых функций формулами. Примеры:
- •7. Разложение булевых функций по переменным. Теорема:
- •10. Правила подстановки и замены:
- •13. Замкнутые классы. Свойства замыкания.
- •16.Принцип двойственности
- •17.Класс монотонных ф-ций:
- •19.Алгебра Жегалкина.
- •27. Высказывания.
- •28.Интерпретация формулы. Теорема.
- •29. Логическое следование и логическая эквивалентность.
- •30. Логические эквивалентности. Доказательство
- •31. Исчисление высказываний
- •32. Понятие предиката
- •33. Понятие квантора. Квантор существования. Квантор всеобщности
- •34. Исчисление предикатов
- •35. Аксиомы исчисления предикатов:
- •36.Графы. Типы задач теории графов.
- •37.Графы. Основные понятия.
- •38 Способы представления графов:
- •38. Способы представления графов
- •40 Обходы графов. Алгоритмы поиска в глубину и в ширину. Теорема о поиске в глубину и ширину.
- •43. Маршруты, цепи, циклы.
- •44.Связные компоненты графа.
- •45.Расстояния.
- •Диаметр, радиус, центр графа.
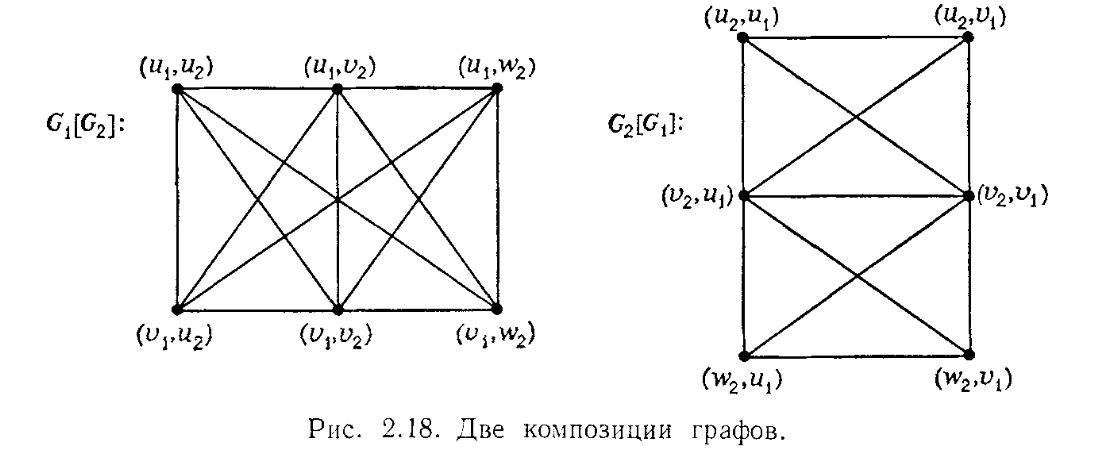
- •47.Произведение графов
- •48. Прямое произведение графов.
- •49.Эйлеровы циклы.
- •Некоторые классы графов и их частей.
- •Концевые вершины и ребра
- •55. Дерево с корнем. Ветви.
- •56.Типы вершин дерева
- •57. Центры деревьев
- •62.Деревья
- •63. Способы обхода деревьев
Диаметр, радиус, центр графа.
Пусть задан граф G конечный, не ориентированный, связный. Диаметр графа G определяется максимальным расстоянием между вершинами V' и V'': d(g)=max d(V’;V’’). Кратчайшие простые цепи, связывающие вершины V' и V'' с максимальным расстоянием между ними называются диаметральными простыми цепями. Пусть V – произвольная вершина графа G. Максимальным удалением от вершины V называется величина r(V)=max d(V,V’). Вершина V называется центром графа, если максимальное удаление от нее принимает минимальное значение. Максимальное удаление от центра графа называется радиусом графа.
47.Произведение графов
Пусть G и Н - два графа(ор или неор) без кратных ребер содним и тем же мн-вом вершин V. Произведением графов G и Н называется граф F = HxG, в котором ребро (V', V'') сущ в том и только в том случае для некоторой вершины V сущ ребра (V', V ) и (V , V”) причем (V',V) e G и (V,V”) e H, т.е сущ маршрут с началом в V' и концом в V”. Причем 1ый элемент маршрута обязательно принадлежит графу G, а 2ой - H. Произведение G и H описывается матрицей смежности, которая равна произведению матрицсмжности сомножителей, только вместо алг необх рассматривать логические операции: eij(F) = V(eik(G). ekj(H))
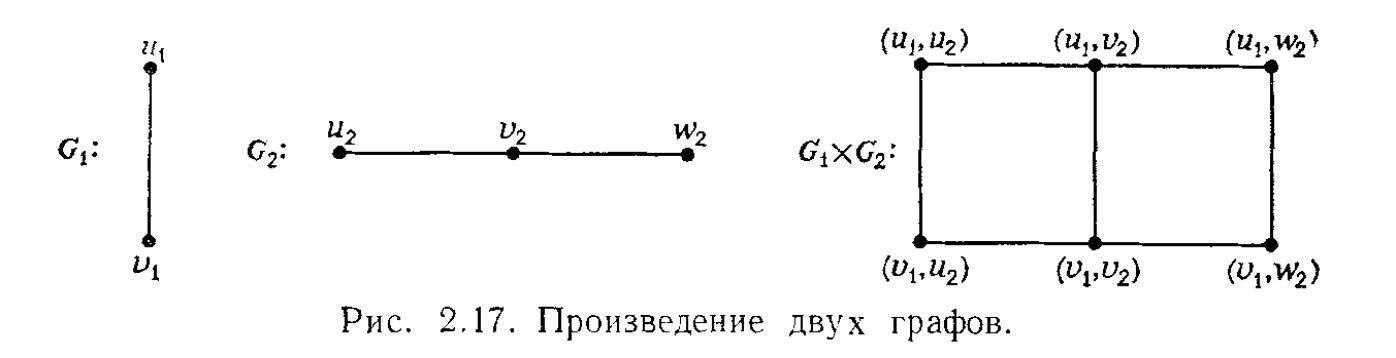
48. Прямое произведение графов.
Множество вершин прямого произведения двух графов G и V задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:
(g, h)(g1, h), где g и g1 — соединённые ребром вершины графа G, а h — произвольная вершина графа H;
(g, h)(h, h1), где g — произвольная вершина графа G, а h и h1 — соединённые ребром вершины графа H.
Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.
49.Эйлеровы циклы.
Пусть G=(V,E)- граф. Цикл, который включает все ребра и вершины графа G, называется эйлеровым циклом, т. е. это такой цикл, который проходит ровно один раз по каждому ребру.
Цикл, содержащий все ребра мультиграфа называется эйлеровым, и мультиграф, в котором имеется эйлеров цикл, также называется эйлеровым.Цепь, содержащая все ребра графа называется эйлеровой. Связанный неориентированный мультиграф тогда и только тогда эйлоровым, когда степень каждой из его вершин – четное число. Связный неориентированный граф G содержит Эйлеров цикл тогда и только тогда, когда число вершин нечетной степени равно нулю. Не все графы имеют Эйлеровы циклы, но если Эйлеров цикл существует, то это означает, что, следуя вдоль этого цикла, можно нарисовать граф на бумаге, не отрывая от нее карандаша.
Алгоритм построения эйлерова цикла в эйлеровом мультиграфе:
выбрать некоторую вершину а
выбрать некоторое ребро u, инцидентная а, и присвоить ему номер1 (пройденное ребро).
Каждое пройденное ребро вычеркнуть и присвоить ему номер на 1 больше номера предыдущего вычеркнутого ребра.
Находясь в вершине х не выбирать ребро соединяющее х с а, если имеется возможность иного выбора.
Находясь в вершине х не выбирать ребро, которое является перешейком (т.е. ребром, при удалении которого граф, образованный не вычеркнутыми ребрами распадается на две компоненты связанности, каждая из которых имеет хотя бы по 1 ребру).
50.Теорема Эйлера Цикл графа G, содержащий все его рёбра, наз. эйлеровым. Граф, имеющий эйлеров цикл наз. эйлеровым.
Терорема.
Для каждого связного графа G следующие условия эквивалентны:
1.)G – эйлеров граф.
2.)Каждая вершина графа G имеет чётную степень.
3.)Мн-во рёбер графа можно разбить на простые циклы, т.е. U=ki=1 ui (ui uj=, (ij), ui=).
Доказательство.
Пусть G – эйлеров граф. Покажем, что каждая вершина имеет чётную степень. Каждая вершина простого цикла имеет степень 2. Поэтому, если в графе G существует эйлеров цикл, то каждая вершина должна иметь чётную степень.
Пусть каждая вершина имеет чётную степень. Выбираем произвольную вершину графа i1 и движемся от неё по ребру к смежной вершине i2, и т.д. каждый раз выбирая новое ребро. Т.к. граф связен, число рёбер в графе конечно и войдя в вершину по некоторому ребру мы можем выйти по другому, то через некоторое число шагов какая-то вершина ik повторится. Тогда i1,i2,…,ik,i1 образует простой цикл в исодном графе (u1). Удалим рёбра этого цикла из исходного графа. Новом графе каждая не изолированя вершина имеет чётную степень, поэтому процедуру выделения простых циклов можно применять к каждой компоненте связности, отличной от изолированой вершины. Через некоторое число шагов мы получим исх. разбиение.
Пусть закдано разбиение U=ki=1 ui. Покажем, что эйлеров цикл. Т.к. G – связный граф, то найдутся два простых цикла имеющих общую вершину эти два цикла можно объеденить (склеить) в один цикл. Пусть u’ и u’’ имеют общую вершину k. u’=(j1,j2,…,jl-1,k,j1+1,…,jm,j1), u’’=(t1,t2,…,td-1,k,td+1,…,tf,t1), u*=(j1,j2,…,jl-1,k,td-1,…,t1,tf,tf-1,…,td+1,k,j1+1,…,jm,j1). Число циклов при этом уменьшиться на еденицу. Повторяя процедуру склеивания, в итоге получим один цикл, содержащий все рёбра исходного графа – эйлеров цикл, ч.т.д.
Док-во данной теоремы можно использовать в качестве алгоритма при построении эйлерового цикла, если он существует.
51.Эйлеровым путем(цепью) в графе называется путь, проходящий через каждое ребро графа только один раз, т.е. путь v1,v2..., vm+1, такой, что каждое ребро e, принадлежащее E, появляется в последовательности v1, v2..., vm+1 в точности один раз как e={vi,vi+1}. В этом случае говорят, что граф G имеет эйлеров путь. Если граф G связный и А и В единственные нечётные вершины его, то граф G обладает эйлеровым путём с концами А и В.
Задача существования эйлерова пути в заданном графе была решена Л.Эйлером в 1736 г., и представленное им необходимое и достаточное условие существования такого пути считается первой в истории теоремой теории графов.
Если эйлеров путь не является эйлеровым циклом, то такой путь назы-
вают собственным эйлеровым путем.
ТЕОРЕМА. Граф (мультиграф или псевдограф) имеет собственный
эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины
имеют нечетную степень.
Пример 1. Рассмотрим граф
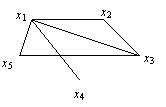
Он имеет эйлеров путь (x4, x1, x3, x2, x1, x5, x3).
Пример2. Граф имеет собственый Эйлеров путь.
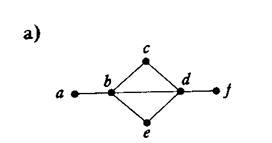
Эйлеров путь (эйлерова цепь) в графе — это путь, проходящий по всем рёбрам графа и притом только по одному разу.
Эйлеров цикл — это эйлеров путь, являющийся циклом.
Эйлеров граф — граф, содержащий эйлеров цикл.
Полуэйлеров граф — граф, содержащий эйлеров путь (цепь).
Эйлеров цикл/путь существуют только в связных графах или в графах, которые после удаления всех одиночных вершин превратятся в связные.
Теорема:
О риентированный
граф содержит эйлеров цикл тогда и
только тогда, когда он сильно-связан и
для каждой вершины графа её полустепень
захода равна её полустепени исхода, то
есть в вершину входит столько же ребер,
сколько из неё и выходит.
риентированный
граф содержит эйлеров цикл тогда и
только тогда, когда он сильно-связан и
для каждой вершины графа её полустепень
захода равна её полустепени исхода, то
есть в вершину входит столько же ребер,
сколько из неё и выходит.
Пример:
52 Гамильтонов граф — в теории графов это граф, содержащий гамильтонову цепь или гамильтонов цикл.
Гамильтонов путь (или гамильтонова цепь) — путь (цепь), содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная и конечная вершины которого совпадают, называется гамильтоновым циклом. Гамильтонов цикл является простым остовным циклом.
