19.Алгебра Жегалкина.
20 Теорема (Жегалкин)
Любая булева функция представляется в виде полинома Жегалкина, причем единственным образом с точностью до порядка следования элементарной конъюнкции (слагаемых) и до порядка следования переменных в элементарных конъюнкциях.
Доказательство. Если функция , то полиномом Жегалкина для данной функции является константа 0. В остальных случаях представим функцию в виде СДНФ:
Преобразуем СДНФ в полином Жегалкина. Прежде всего, все знаки дизъюнкции можно заменить на знак суммы по модулю 2 :
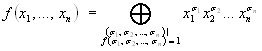
Это можно сделать
по следующей причине: дизъюнкция
.
Если х и у заменить элементарными
конъюнкциями из СДНФ, то получим
.
так как
.
Действительно
и
имеют одинаковые наборы переменных,
которые отличаются только расстановкой
отрицания, поэтому в произведении
найдется переменная
,
которая встречается с отрицанием и без
отрицания. А конъюнкция таких переменных:
равна нулю:
Далее
в полученной формуле преобразуем
отрицания по формуле:
.
После этого останется раскрыть скобки,
что можно сделать ввиду следующего
дистрибутивного закона:
.
После раскрытия всех скобок мы получим
сумму элементарных конъюнкций без
отрицаний. Если среди полученных
конъюнкций есть одинаковые, то все их
(за исключением, может быть, одной из
группы одинаковых) можно убрать по
следующему правилу:
.
В итоге получим полином Жегалкина.
23 Лема о нелинейных ф-циях: Если ф-ция нелинейна, то из нее путем подстановки вместо переменных, констант, тождественной ф-ции и отрицания самой ф-ции можно получить коньюнкцию.
Док-во: Пусть fL. Тогда в ее представлении в виде полинома Жегалкина имеется наименьшее слагаемое. Будем предполагать, что в это слогаемое входят переменные x1 и x2. Тогда (3, 4,…,n):
f(x1, x2, 3, 4,…,n)=x1x2x1x2.
(в противном случае, переменные x1, x2 были бы фиктивными).
(x1, x2)= x1x2x1x2.
По ф-ции построем ф-цию S:
S(x1, x2)=(x1, x2).
Можно показать, что S(x1, x2)=x1&x2.
|
T0 |
T1 |
S |
M |
L |
1 |
- |
+ |
+ |
+ |
+ |
x |
+ |
+ |
+ |
+ |
+ |
x |
- |
- |
- |
- |
+ |
Из таблицы видно, что основные замкнутые классы попарно не совпадают.
21 Полнота Рассмотрим множество булевых функций M={f1f2,fn}, назовем его системой логических функций.
Определение 1. Множество M={f1f2,fn} является полной системой, если любую булеву функцию можно представить формулой над М.
Другими словами, система будет полной, если любую функцию можно представить
суперпозицией функций f1, f2,, fn . Чтобы разобраkться, приведем пример из обычной математики. Функцию возведения в степень f(x)=x можно представить через функцию умножения f(x)=xk=ххх, проделав операцию умножения k раз. Аналогично, булевы функции представимы через другие булевы функции.
Приведем примеры:
{,, } - конъюнкция, дизъюнкция и инверсия образуют полную систему (значок
обозначает инверсию);
{ , } - конъюнкция и инверсия также образуют полную систему;
{/} - полная система может содержать всего одну функцию, например Штрих Шеффера.
Мы можем дать еще одно определение полной системы.
Определение 2. Система М называется полной, если ее замыкание есть множество всех булевых функций
22Лема о немонотонных ф-циях: Если ф-ция f немонотонна, то из нее путем подстановки вместо переменных констант и тождественной ф-ции можно подставить отрицание.
Пусть fM т.е. <: f()<f(), поэтому f()=1, f()=0. Покажем, что найдутся два соседних набора (по некоторой переменной) и такие, что <, а f()>f(). Предположим обратное: пусть < и они отличаются, например, по первым t переменным.
=(0, 0, …, 0, t+1,…,n)
=(1, 1, …, 1, t+1,…, n)
По и построим последовательность наборов (0)=, (1) – соседний с (0) по 1-й переменной, (2) – по 2-й переменной и т.д., (t)=.
=(0)<(1)<…<(t)=, причем f((0))>f((t)), поэтому в этой последовательности найдутся два соседних набора (i)<(i+1), а f((0))>f((i+1)).
Поэтому будем предпологать, что и – два соседних набора, для которых нарушается монотонность. Эти наборы можно найти по таблице истинности. Построим ф-цию (x)=( 1,…,i-1,x,i+1,…,n) (наборы и соседние по х).
(0)=( 1,…,i-1,0,i+1,…,n)=f()=1
(1)=( 1,…,i-1,1,i+1,…,n)=f()=0
т.е. (x)=x ч.т.д.
25
.