63. Способы обхода деревьев

рассмотрим задачу. Необходимо осуществить обход графа следующим образом: выйти из вершины А, обойти все остальные вершины, при этом запрещается посещать их более одного раза, и вернуться в А.

Алгоритмы решения этой задачи имеют итеративный характер при этом количество итераций зависит от стратегии поиска – порядка в котором рассматриваются вершины. Будем использовать список закрытых вершин(ЗКР), который содержит идентификаторы открытых вершин и вершин, которые необходимо раскрыть и список открытых вершин(ОТК), который содержит вершины, которые могут быть раскрыты.

В алгоритме полного перебора вершины просматриваются (раскрываются) в тои порядке в котором были порождены. На каждом этапе проверяется, не является ли достигнутая вершина целевой.

Алгоритм

1) поместить начальную вершину в список ОТК.

2)Если список ОТК пуст, то сообщить о неудаче.

3) Взять вершину из ОТК, перенести в список ЗКР, присвоить вершине идентификатор V .

4) рассмотреть вершину V , поместить все её дочерние вершины (не встречающиеся ещё в ЗКР) в ОТК и построить указатели, ведущие от них к вершине V. если V не имеет дочерних вершин, то перейти к шагу 2.

5)проверить, не является ли одна из дочерних вершин вершины V – целевой. если да – выдать решение, иначе – прейти к шагу 2.

в этом алгоритме предполагается, что начальная вершина не есть целевой.

алгоритм позволяет найти все решения, а если суммировать длины путей, то среди всех решений можно найти оптимальный.

Алгоритм равных цен позволяет осуществить направленный поиск, является обобщением алгоритма полного перебора и сводится к нему при одинаковой стоимости путей.

стоимость раскрытия вершины – длина связующего ребра дочерней и родительской вершин. Обозначим её , где i –родительская вершина, j – дочерняя.

Алгоритм

1. поместить начальную вершину в список ОТК.

2. Если список ОТК пуст, то сообщить о неудаче.

3. Взять вершину из ОТК, перенести в список ЗКР, присвоить вершине идентификатор V .

4. Если глубина вершины равна граничной глубине, то прейти к шагу 2.

5. Раскрыть вершину V , поместить все дочерние вершины в ОТК, построить указатели, ведущие от них к вершине V. если V не имеет дочерних вершин, то перейти к шагу 2.

6. Если одна из вершин является целевой – выдать решение, иначе – идти к 2.

Глубина вершины . Если на ребрах отсутствуют веса, то в качестве условия ограничения может быть поставлена глубина прохода по дереву, которая определяется количеством уровней в дереве. Этот алгоритм может быть применен для обхода дерева в глубину. В общем случае он реализует направленный поиск в дереве.

66 Бинарное дерево – структура, которая содержит конечное множество узлов, состоит из корня и 2х непересекающихся поддеревьев, которые также являются бинарными деревьями.

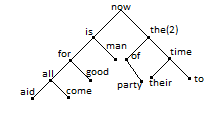
Необходимо определить встречаемость каждого слова во входном потоке информации. Поскольку список слов заранее неизвестен, то нет возможности его предварительно упорядочить, а следовательно нет возможности применить к нему бинарный поиск. Линейный поиск является малоэффективным. Для организации более эффективного поиска можно использовать структуру бинарного дерева. При этом помещать каждое вновь полученное слово в эту структуру таким образом, чтобы не нарушалась предварительная упорядоченность. Для этого будем использовать структуру бинарного дерева.

В бинарном дереве, для хранения каждого слова будем использовать вершину дерева, а она же будет содержать следующую информацию: идентификатор, он содержит указ. на текст слова, счетчик числа встречаемости, указатель на левое поддерево, правое поддерево.

Now is the time for all good man to come the aid of their party.

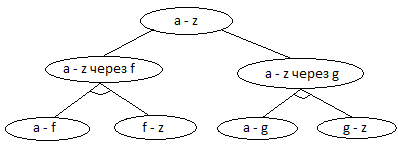
67«И-или» дерево – структура, которая содержит конечное число узлов, имеет корень, который в общем случае реализует некоторый составной объект и вершины 2х типов: типа «И», которые являются обязательными к включению в обход дерева, и типа «Или», которые являются альтернативными при включении в обход дерева.

Обход «И-или» дерева должен включать корневую вершину, все вершины типа «И» и возможные вершины типа «Или».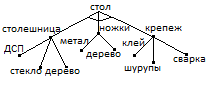

«И-или» дерево – один из подходов, используемый для представления пространства поиска решения задач технического творчества и искусственного интеллекта. Представление в виде «И-или» дерева наиболее приемлемо для задач, которые естественным образом разбиваются на взаимнонезависимые задачи, символического интегрирования, доказательства теорем и, в частности, задач поиска технических решений.

68 Обход «И-или» дерева должен включать корневую вершину, все вершины типа «И» и возможные вершины типа «Или».

Необходимо из вершины а попасть в z.

Для обхода «И-или» деревьев в общем случае могут быть использованы алгоритмы полного перебора, однако предпочтительнее является некоторый направленный поиск, который ограничивается условием решающего дерева.

Стоимость вершин определяется как сумма стоимостей ребер, необходимых для достижения вершины.

Введем понятие трудности достижения вершины, которую будем оценивать при помощи функции h. Эти оценки будут использоваться для управления процессом поиска. Поиск будет продовжаться в том напрвлении, в котором существует найболее перспективное дерево-кандидат.

Введем функцію H, которая будет характеризовать оценку трудности вершины В.

Для корневой вершины: Н(В) = h(В)

Для оценки трудности вершины типа «или», которая является внутренней, будем использовать следующую оценку: g(Bn) = g(Bn-1) + C(Bn-1B)

H(B) = min(h(B) + C(B,Bi))

Для вершины типа «И»

H(Bn) = ∑C(BB1) + h(B)

Для ограничения поиска будем использовать оценки. Дан граф:

d, g, h – целевые.

H(b) = 1; H(c) = 3.

Поиск продолжается в том направлении, в котором стоимость меньше, до тех пор, пока оценка вершины в этом направлении не станет больше чем оценка вершины-конкурента.

Нормальным упорядочением вершин орграфа называется такое их упорядочение, при котором всегда (i1, i2 ... in) если имеется пара (ik; in), то вершина ik в упорядочении стоит раньше in. В общем случае имеет место не одно нормальное упорядочение для графа.

Теорема: Пусть задан орграф G = (V,E), тогда следующие утверждения являются эквивалентными.

1) Граф G — безконтурный.

2) Граф G обладает рекурентными свойствами нормальной упорядочености: если множество вершин графа не пусто, то существует вершина не имеющая входящих дуг и после удаления такой вершины обновленный граф также будет иметь свойства нормальной упорядочености.

3) Множество упорядочений графа G не пусто.

Существуют два основных метода представления графов в памяти ЭВМ: матричный, т.е. массивами, и связными нелинейными списками. Способы представления матричным методом: матрица смежности, массив ребер, матрица инцидентности, списки смежности.

Матрица инцидентности — одна из форм представления графа, в которой указываются связи между инцидентными элементами графа (ребро(дуга) и вершина). Столбцы матрицы сответствуют вершинам, строки — ребрам. Ненулевое значение в ячейке матрицы указывает связь между вершиной и ребром (их инцидентность). В каждой строке должны стоять две единицы, а все остальные символы - нули.

Пример

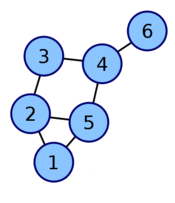
Матрица смежности графа G с конечным числом вершин n — это квадратная матрица A размера n, в которой значение элемента aij равно числу ребёр из i-й вершины графа в j-ю вершину. Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i-й вершины. Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали. Матрица смежности полного графа Kn содержит единицы во всех своих элементах, кроме главной диагонали, на которой расположены нули. Матрица смежности пустого графа, не содержащего ни одного ребра, состоит из одних нулей. Степени матрицы. Если A — матрица смежности графа G, то матрица A в степени m обладает следующим свойством: элемент в i-й строке, j-м столбце равен числу путей из i-й вершины в j-ю, состоящих из ровно m ребер.

Пример

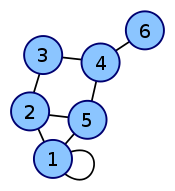
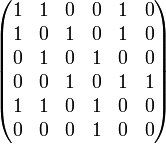
Списки смежности. Представляет собой структуру данных, которая для каждой вершины графа хранит список смежных с ней вершин. Список представляет собой массив указателей, i-ый элемент которого содержит указатель на список вершин, смежных с i-ой вершиной. Список смежности более эффективен по сравнению с матрицей смежности, так как исключает хранение нулевых элементов.

Теорема(Эйлера формула)

Если G связный планарный граф, содержащий V вершин, e ребер и f граней, то V-e=f=2

Доказательство

Докажем формулу Эйлера по индукции по числу ребер в

7. Пусть е=0, тогда V=1, f=1 формула действительна

Пусть е=1, тогда V=2, f=1 формула действительна

8. Индукциальная гипотеза:

Предположим, что теорема верна для произвольного связного планарного графа, у которого k ребер.

9. Индукционный переход

Пусть задан G_k+1 , имеющий е= k+1. Проверим выполнимость формулы для этого графа. Удалим одно ребро графа G_k+1, так что в результате будет получен граф G_k , для которого выполняется формула.

А. Предположим что граф G_k+1 не имеет циклов. Будем перемещаться вдоль по пути до тех пор, пока не достигнем вершины, у которой нет другого выходящего ребра. Это обязательно произойдет, так как граф не содержит циклов, найденная вершина будет иметь степень 1. Удалим ее и ребро, инцидентное ей. Очевидно, что f не изменится. При этом граф останется связным, планарным, а значит формула выполняется. Поскольку количество вершин и ребер начального графа >1 , то значение выражения V-e=f=2 после процедуры удаления останется неизменным. Таким образом для G_k+1, V-e=f=2 и в этом случае теорема доказана.

Б. Граф G_k+1 имеет цикл. Удалим из него ребро е и инцидентное вершинам V_і и U_i . Очевидно, что е_і не является разрезающим, таким образом между V_і и U_i остаётся путь и граф связный. Граф также останется планарным и содержит k ребер. Поэтому для оставшегося графа по индукциальной гипотезе формула выполняется. Покажем что она выполняется и для графа G_k+1. Поскольку е і входило в цикл, она разделяло 2 грани. поэтому V-e=f=2 не изменилось, формла справедлива и для G_k+1.

Для доказательства того, что полный двудольный граф К₃₃ является моделью задачи о трех домах и трех колодцах, не может быть изображен без пересечения ребер.

Т2:Полный двудольный граф К₃₃ не является планарным

Доказательство.

Предположим, что К₃₃ планарен. В графе V=6 е=9. Если он планарен, то по формуле Эйлера 6-9+ f=2 он имеет 5 граней. Пусть А и В не пресекается непересекающиеся мноножества вершин формирующие V графа графа К₃₃ V=АvВ .

Если начать путь из одного из непересекающихся множества А и не повторять ребра, то можно попасть в вершину из множества В вернуться в А , вернуться в В, попасть в А вернуться в Ви завершить цикл. Таким образом каждый цикл в К₃₃ представляет собой путь длинны U. Поэтому каждая грань определена циклом в котором не менее 4 ребер. Следовательно, сумма ребер во всех гранях > f. Однако каждое ребро пренадлежит граням U учитывается не более 2-х раз. Значит сумма ребер всех граней <2e . полученые неравенства объеденим 4f<=2e => f<=4. Это противоречит f=5.

Для доказательства того, что К5 не планарен сформулируем и докажем лемму.

Лемма 1:

В производном связном планарном графе G с V>3 имеет место3V-e>=6

Доказательство

Пусть G имеет цикл. Будем суммировать ребра, ограничивающее грани в G. Поскольку каждая грань включает не менее 3 ребер, то сумма всех граней > 3f. С другой стороны каждое ребро является границей двух граней. Поэтому сумма всех ребер <2е. Следовательно 3f<=2e. Так как граф связный и планарный, справедлива формула Эйлера

V-e=f=2

3V-3e+3f<=3V-3e+2e

3V-3e+3f<=3V-e

3V-e>=6

Т:Полный граф К5 не планарен.

Доказательство

Граф К5 связний и имеет количество ребер e=n(n-1)/2

е=10 V=5

Таким образом по предыдущей лемме

3V-e>=6 К5 – не планарен

Т: Каждый планарный граф содержит вершину V степени 5 или менее.

Доказательство

Каждое ребро графа имеет 2 вершины. Таким образом оно вносит 2 ед в сумму степеней всех вершин.

Если в графе не более 2-х вершин, то очевидно каждая из них имеет 5 или менее. Пусть в графе 3 или более вершин. Тогда по лемме 1 3V-e>=6. Таким образом, если предположить, что степень каждой вершины >=6, то сумма степеней всех вершин >= 6V, но по условию 2е >=6 V, но это невозможно, поскольку 2е <=6V-12, следовательно существует вершина со степенью 5 или меньше.

Лемма2 :

Если 2 связных графа гомеоморфны, то они оба либо планарны, либо оба не планарны.

Лемма3:

Произвольный граф, гомеоморфный графу К33 или К5 непланарен

Теорема Куратовского:

Граф G является планарным тогда и только тогда, когда он не содержит подграф, гомеоморфный графу К33 или К5.