Лабораторная работа №16 Решение нелинейных уравнений численными методами
При решении инженерных задач встречаются алгебраические и трансцендентные уравнения, что может представлять собой самостоятельную задачу или являться составной частью более сложных задач. В обоих случаях применение численного метода позволяет быстро и эффективно добиться решения задачи.
Линейные уравнения имеют одно решение, алгебраические уравнения – n решений, трансцендентные – неопределённое число решений. Решение линейных уравнений с одним неизвестным является достаточно простой задачей и здесь не рассматривается.
Уравнения, содержащие
только суммы целых степеней x,
называются алгебраическими. Их общий
вид
.
Нелинейные уравнения, содержащие тригонометрические функции или другие специальные функции, например lg x или ex, называются трансцендентными.
Для решения нелинейных уравнений, для которых отсутствует аналитическое решение или оно очень сложно, применяют численные методы, в которых, как правило, применяются итерационные алгоритмы. В итерационных методах задаётся процедура решения в виде многократного применения некоторого алгоритма. Полученное решение всегда является приближённым, хотя может быть сколь угодно близким к точному.
В общем случае задача формулируется следующим образом.
Пусть на отрезке [a,b] дана непрерывная функция y=f(x), причем значения f(a) и f(b) имеют разные знаки. Тогда абсцисса точки пересечения графика функции y=f(x) с осью x будет корнем уравнения f(x)=0, см. рис.16.1. Другими словами, требуется найти такое значение x, при котором значение функции f(x) будет равно нулю.
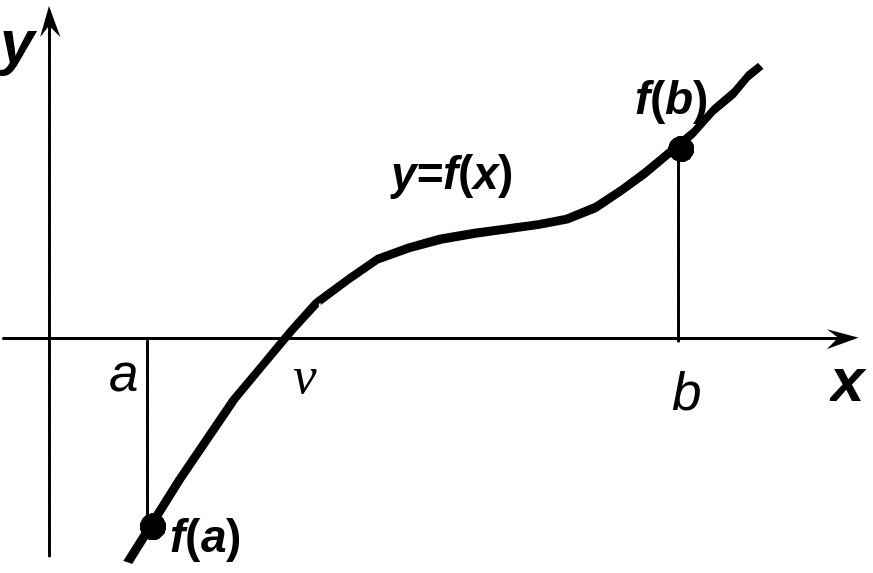
Рис.16.1. Графическая интерпретация нахождения корня уравнения
Численными методами значение корня определяется с погрешностью, не превосходящей данного положительного, достаточно малого числа . Иначе говоря, если v – истинное значение корня, при котором f(v)=0, то требуется определить такое число w, при котором awb и vw.
Первый этап решения состоит в отыскании области существования корня, т.е. отрезков на оси абсцисс, в концах которых функция имеет разные знаки. Для этого вычисляются значения функции в точках, расположенных через равные интервалы на оси x. Это делается до тех пор, пока не будут найдены два последовательных значения функции f(xn) и f(xn+1), имеющих противоположные знаки, т.е. f(xn)f(xn+1)<0. Таким образом, при a= xn, b=xn+1, уточнение корней будет производиться на отрезке [a,b].
Для решения данной задачи применяются методы: половинного деления, касательных (Ньютона), хорд и секущих.
Метод половинного деления
Алгоритм метода состоит из следующих операций.
Отрезок [a,b] делят пополам точкой c (c=(a+b)/2) и находят значение функции в точке с. Если f(c)=0, то корень уравнения соответствует точке c. Если f(c)0, то можно сузить диапазон поиска корня: перейти от отрезка [a,b] к отрезку [a,c] или [c,b] в зависимости от знака f(c). Если f(a)f(c)<0, то корень находится на отрезке [a,c], и точку с будем считать точкой b; а если f(a)f(c)>0, то корень находится на отрезке [c,b], и точку с будем считать точкой a.
Каждый такой шаг уменьшает в два раза интервал, в котором находится корень уравнения f(x)=0. После нескольких шагов получится отрезок, длина которого будет меньше или равна числу , т.е. ab. Любая точка такого отрезка, например, один из его концов, подходит в качестве решения поставленной задачи. На рис. 16.2 показано несколько этапов применения алгоритма.
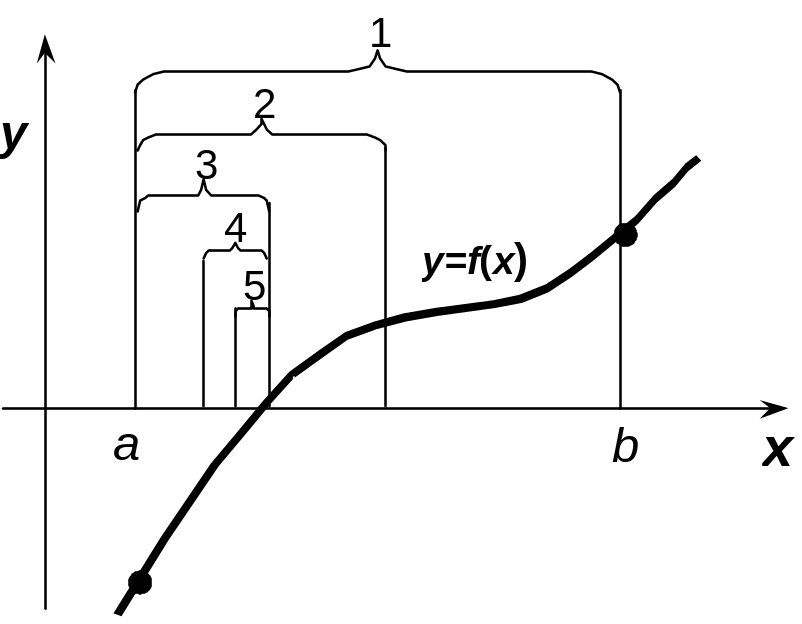
Рис.16.2. Графическая иллюстрация метода половинного деления: 1…5 – интервалы уточнения корней на 1...5 шаге алгоритма
Пример 1. Найти с точностью =0,001 на отрезке [-2,1] корень уравнения x3+x2+x+1=0. Приведём текст программы, которая решает эту задачу методом половинного деления (результат выводится на экран и, по желанию пользователя, на принтер):
Program Popolam;
Uses Crt, Printer;
Var
a,b,c,eps,a0,b0:real;
k:integer;
ch:char;
Function f(x:real):real;
begin
{ Здесь приводим выражение для вычисления функции }
f:=x*x*x+x*x+x+1;
end;
Begin
ClrScr;
Writeln(' Решение уравнения методом половинного деления ');
{ Ввод исходных данных }
a:=-2; b:=1; eps:=0.001;
a0:=a; b0:=b; { Запоминаем исходные данные }
{ Начинаем расчет }
k:=0; { Счетчик повторений }
While abs(b-a)>=eps do
begin
k:=k+1;
c:=(a+b)/2;
if f(a)*f(c)<=0 then b:=c
else a:=c;
end;
Writeln(' Уравнение x^3+x^2+x+1=0 на отрезке [',a0:4:1, ',', b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(' f(x) = ',f(c):10:8);
Writeln('Точность ',eps:10:8, ' достигнута за ', k,' итераций');
Write(' Печатать результаты на принтере? (Y/N)');
Repeat
ch:=ReadKey;
ch:= UpCase(ch);
Until (ch='Y') or (ch='N');
if ch='Y' then
begin
Writeln(lst,'Решение уравнения методом половинного деления');
Writeln(lst,' Уравнение x^3+x^2+x+1=0 на отрезке [', a0:4:1, ',', b0:4:1, '] имеет корень x = ', c:10:8);
Writeln(lst,' f(x) = ',f(c):10:8);
Writeln(lst,' Точность ',eps:10:8, ' достигнута за ', k,' итераций');
Writeln('Печать выполнена. Нажмите ENTER ');
Readln;
end;
End.