Задания
1. Набрать текст программы Popolam. Провести вычисления и вывести на принтер (экран) результаты расчётов при = 0,1; 0,01; 0,0001; 0,00001. Сравнить результат и количество итераций.
2. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом касательных. Сравнить результат и количество итераций при = 0,1; 0,01; 0,001; 0,0001.
3. Сохранить под другим именем и модифицировать программу, чтобы она решала уравнение методом хорд. Сравнить результат и количество итераций при = 0,1; 0,01; 0,001; 0,0001.
4. Сохранить под другим именем и используя три предыдущих примера, модифицировать программу, чтобы последовательно методом половинного деления, хорд и касательных уточнить корень уравнения (см. табл.), расположенный на интервале [a,b], с абсолютной погрешностью . Определить также число итераций, необходимое для нахождения корня. Сравнить результат при = 0,1; 0,01; 0,001; 0,0001; 0,00001. Результаты должны выводиться в виде таблицы:
Результаты решения уравнения различными методами
Точность |
Деления пополам |
Касательных |
Хорд |
0,1 |
|
|
|
0,01 |
|
|
|
0,001 |
|
|
|
0,0001 |
|
|
|
0,00001 |
|
|
|
Варианты задания
Вариант задания |
Уравнение |
Отрезок |
1 |
x2+10x=0 |
[0; 1] |
2 |
|
[2; 3] |
3 |
x – 2+sin(1/x)=0 |
[1,2; 2] |
4 |
1 – x + sin x – ln(1+x)=0 |
[0; 1,5] |
5 |
x2 – ln(1+x)–3=0 |
[2; 3] |
6 |
2x – 3 ln x – 3=0 |
[0,5; 0,6] |
7 |
ln x – x + 1,8=0 |
[2; 3] |
8 |
0,1x2–x ln x=0 |
[1; 2] |
9 |
x+cos(x0,52+2)=0 |
[0,5; 1] |
10 |
3x – 4 ln x – 5=0 |
[2; 4] |
Лабораторная работа №17 Решение обыкновенных дифференциальных уравнений численными методами
Дифференциальными называются уравнения, содержащие одну или несколько производных. Поскольку большая часть законов физики формулируется именно в виде дифференциальных уравнений, то инженеру приходится сталкиваться с ними. Лишь немногие из них удаётся решить без помощи вычислительных машин. Поэтому численные методы решения дифференциальных уравнений играют важную роль в практике инженерных расчётов.
Чтобы решить обыкновенное дифференциальное уравнение, необходимо знать значения зависимой переменной и (или) её производных при некоторых значениях независимой переменной. Если дополнительные условия задаются при одном значении независимой переменной, то такая задача называется задачей с начальными условиями или задачей Коши. Если же условия задаются при двух или более значениях независимой переменной, то такая задача называется краевой. В задаче Коши дополнительные условия называются начальными, а в краевой задаче – граничными.
Рассмотрим способы решения задачи Коши, которая формулируется следующим образом. Пусть дано дифференциальное уравнение
и начальное условие
y(x0)=y0.
Требуется найти функцию y(x), удовлетворяющую как указанному уравнению, так и начальному условию. Искомая функция выражается в табличном виде:
x0 |
x1 |
x2 |
x3 |
… |
xn |
y0 |
y1 |
y2 |
y3 |
… |
yn |
Значения x вычисляются через малое приращение h, h=x0–x1=x2–x1.
Обычно численное решение этой задачи получают, вычисляя сначала значение производной, а затем, задавая малое приращение для x, переходят к новой точке x1=x0+h. Положение новой точки определяется по наклону кривой, вычисленному с помощью дифференциального уравнения. Таким образом, график численного решения представляет собой последовательность коротких прямолинейных отрезков, которыми аппроксимируется истинная кривая y=f(x) (рис.17.1). Сам численный метод определяет порядок действий при переходе от данной точки кривой к следующей.
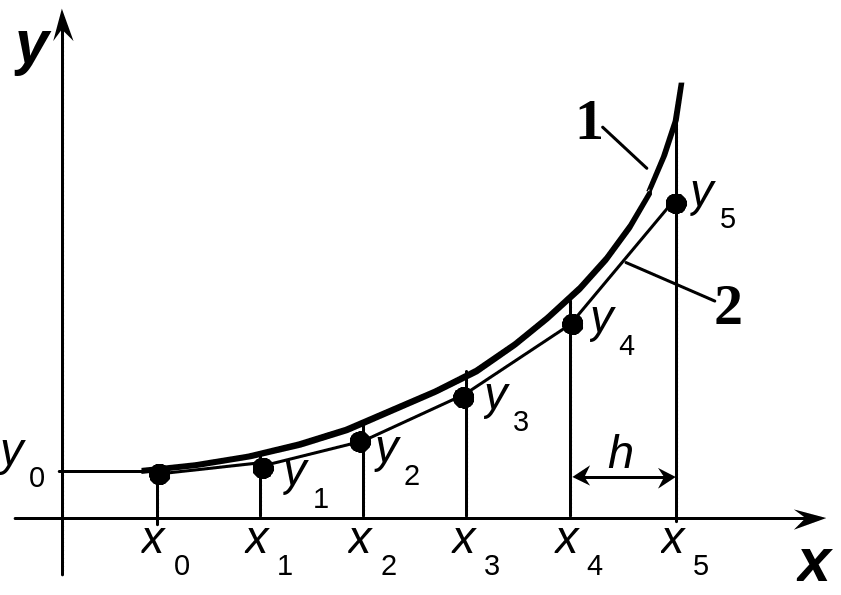
Рис.17.1. Графическое представление численного решения задачи Коши: 1 – точное решение; 2 – решение, полученное численным методом
Наиболее простыми и известными из методов решения задачи Коши являются методы Эйлера и Рунге-Кутта. Они используются для решения дифференциальных уравнений первого порядка вида y=f(x,y), где y=dy/dx, при начальном условии y(x0)=y0.