Метод Эйлера

Это простейший метод решения задачи Коши, позволяющий решить дифференциальное уравнение первого порядка. Его точность невелика, поэтому на практике им пользуются редко. Однако на основе этого метода легче понять алгоритм других, более эффективных методов.

Метод Эйлера основан на разложении функции y в ряд Тейлора в окрестности x₀:

Если h мало, то члены, содержащие производные второго и более высоких порядков, можно отбросить. Тогда . y’(x₀) находим из дифференциального уравнения, подставив в него начальное условие. Таким образом, можно получить приближённое значение y при малом смещении h от начальной точки x₀. Этот процесс можно продолжить, используя следующую рекуррентную формулу:

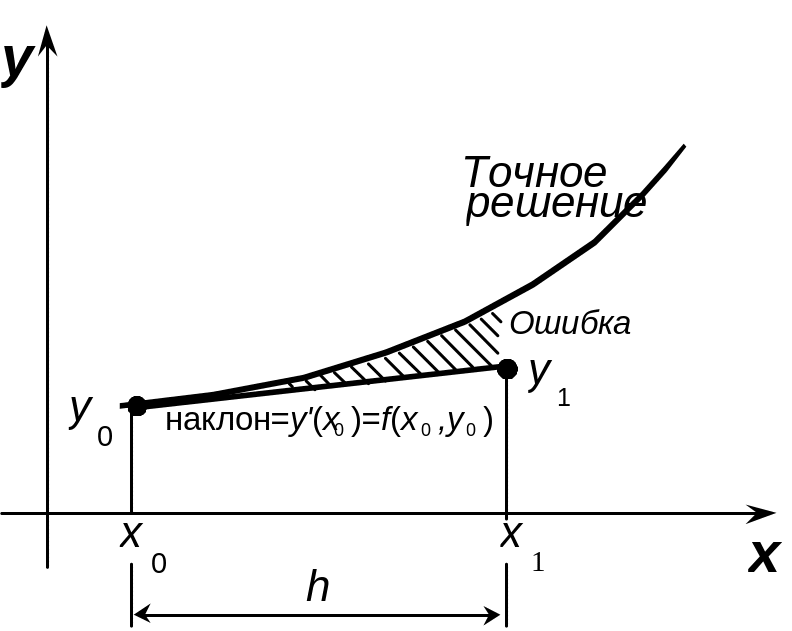
Рис.17.2. Принцип метода Эйлера

y_i+1=y_i + hf(x_i,y_i), i=1,2,…

Графически метод Эйлера показан на рис.17.2. Ошибка метода имеет порядок h².

Пример 1. Составим программу для решения дифференциального уравнения y=2x²+2y при начальном условии y(0)=1; 0 x1 и h=0,1.

Program Euler;

Uses Crt;

Var

xn,xk,yn,h,x,y:real;

i:integer;

Function f(x,y:real):real;

begin

{ Здесь приводим выражение для вычисления функции f(x,y) }

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y методом Эйлера ');

{ Ввод исходных данных }

xn:=0; yn:=1; xk:=1; h:=0.1;

{ Выводим шапку таблицы и первую точку }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

{ Начинаем расчет }

x:=xn; y:=yn; i:=1;

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

Repeat

y:=y+h*f(x,y);

Writeln('|', i:2, ' |', x:5:2, ' |', y:7:4, ' |');

x:=x+h;

i:=i+1;

Until x>xk;

Writeln('--------------------');

Readln;

End.

Модифицированный метод Эйлера

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. Это можно сделать, например, используя среднее значение производной в начале и в конце интервала. В модифицированном методе Эйлера сначала по методу Эйлера вычисляется значение функции в следующей точке:

y^*_i+1 = y_i + hf(x_i,y_i),

которое используется для вычисления приближённого значения производной в конце интервала f(x_i+1, y^*_i+1). Вычислив среднее между этим значением производной и её значением в начале интервала, найдём более точное значение y_i+1:

y_i+1 = y_i + h/2 f(x_i,y_i) + f(x_i+1, y^*_i+1 )].

Принцип метода проиллюстрирован на рис. 17.3. Для получения новой точки в нём требуется информация о двух других точках – предыдущей и промежуточной. Ошибка этого метода на каждом шаге имеет порядок h².

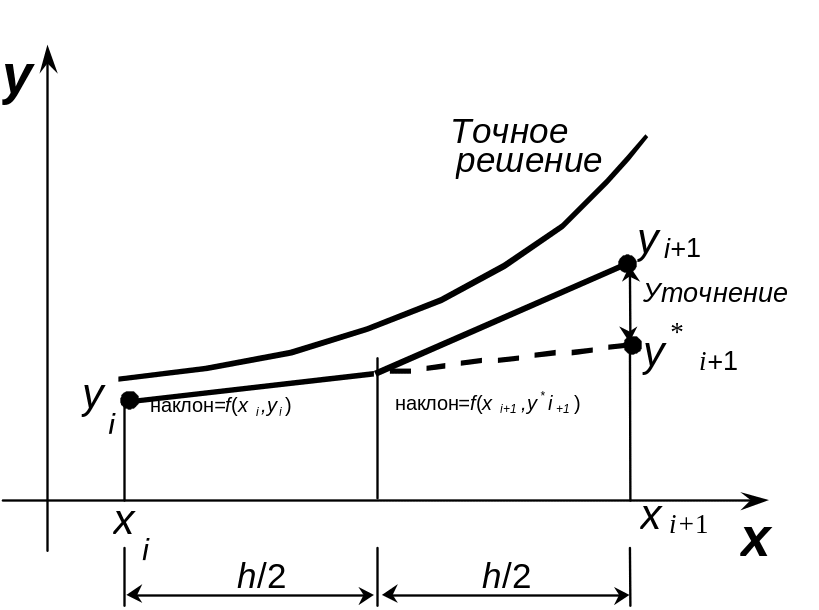
Рис.17.3. Принцип модифицированного метода Эйлера

Пример 2. Разработать, сохранить и выполнить программу для решения дифференциального уравнения из примера 1 модифицированным методом Эйлера (при выполнении расчетов использовать хранение результатов в массивах):

Program ModEuler;

Uses Crt;

Var

xn,xk,yn,yw,h:real;

i,n:integer;

x,y:array [1..20] of real;

Function f(x,y:real):real;

begin

f:=2*x*x+2*y;

end;

Begin

ClrScr;

Writeln(' Решение дифференциального уравнения ');

Writeln(' dy/dx=2x^2+2y модифицированным методом Эйлера ');

xn:=0; yn:=1; xk:=1; h:=0.1;

x[1]:=xn; y[1]:=yn; i:=1;

repeat

yw:=y[i]+h*f(x[i],y[i]);

y[i+1]:=y[i]+h/2*(f(x[i],y[i])+f(x[i]+h,yw));

x[i+1]:=x[i]+h;

i:=i+1;

until x[i]>xk;

n:=i;

{ Выводим результаты }

Writeln('--------------------');

Writeln('| № | x | y |');

Writeln('--------------------');

for i:= 1 to n do

Writeln('|', i:2, ' |', x[i]:5:2, ' |', y[i]:7:4, ' |');

Writeln('--------------------');

Readln;

End.