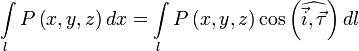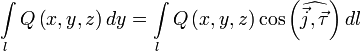Билет 10: Криволинейные и поверхностные интегралы. Вычисление длин кривых и площадей поверхностей. Формулы Грина, Гаусса-Остроградского и Стокса.

Криволинейный интеграл

Пусть   — гладкая, без особых точек и самопересечений кривая (допускается одно самопересечение — случай замкнутой кривой), заданная параметрически.

 - (отрезок параметризации) — рассматриваем часть кривой.

Пусть   — разбиение отрезка параметризации [a, b], причем

Зададим разбиение кривой  .

За   обозначим часть кривой от точки   до точки  ,  .

Введем мелкость разбиения отрезка параметризации  : 

.

Введем набор промежуточных точек разбиения отрезка параметризации l:

.

Зададим набор промежуточных точек разбиения кривой

.

Пусть нам также даны 4 функции, которые определены вдоль кривой  :

  ,  ,  ,  .

Рассмотрим 4 интегральные суммы.

1) Интегральная сумма криволинейного интеграла первого рода:

.

2) Три интегральных суммы криволинейного интеграла второго рода:

,

,

.

Если  , то говорят, что функция   интегрируема в смысле криволинейного интеграла первого рода по кривой  , а сам предел называют криволинейным интегралом первого рода функции   по кривой   и обозначают  . Здесь   — дифференциал кривой.

Если 

,

  ,

  ,

то говорят, что функции  ,   и   интегрируемы в смысле криволинейного интеграла второго рода по кривой  , а сами пределы называют криволинейными интегралами второго рода функций  ,   и   по кривой   и обозначают

Сумму криволинейных интегралов второго рода функций  ,   и   также называют криволинейным интегралом второго рода вектор-функции 

 

и обозначают:

.

Если кривая   замкнута (начало совпадает с концом), то в этом случае вместо значка   принято писать  .

Криволинейный интеграл первого рода

Свойства

1. Линейность:

2. Аддитивность: если   в одной точке, то

3. Монотонность: если   на  , то

4. Теорема о среднем для непрерывной вдоль   функции  :

Очевидно, что: 

.

5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 

.

6. Криволинейный интеграл первого рода не зависит от параметризации кривой.

Вычисление

Пусть   — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция   определена и интегрируема вдоль кривой   в смысле криволинейного интеграла первого рода. Тогда

.

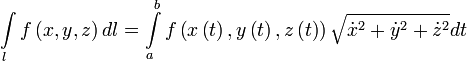Здесь точкой обозначена производная по  :  .

Криволинейный интеграл второго рода

Свойства

1. Линейность:

2. Аддитивность:

3. Монотонность: если на , то

4. Оценка модуля:

5. Теорема о среднем: если   непрерывна на  , то  , такая что: 

6. 

Вычисление

Пусть   — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция   определена и интегрируема вдоль кривой   в смысле криволинейного интеграла второго рода. Тогда

,

,

.

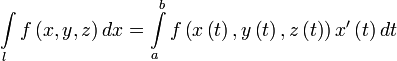Если обозначить за   единичный вектор касательной к кривой  , то нетрудно показать, что

Взаимосвязь криволинейных интегралов

Пусть   — гладкая, спрямляемая кривая, заданная параметрически (как в определении),

   

— единичный вектор, касательный к кривой  .

Пусть также координаты вектор-функции

   

определены и интегрируемы вдоль кривой   в смысле криволинейного интеграла второго рода. Тогда