2. Однородные и неоднородные грунты. Тензор коэффициентов проницаемости грунтов.

В однородных грунтах пористость будет постоянной величиной, в неоднородных грунтах – меняется от точки к точке. Т. о. δ является функцией координат точки.

Если пористость меняется со временем, то такой грунт называется нестационарным. Нестационарность может быть обусловлена закупоркой пор в грунте. Увеличение давления может повлечь за собой увеличение (уменьшение) просветов между частицами грунта. Пористость может зависеть и меняться в результате изменения температуры грунта и температуры жидкости. Изменение этих температур может зависеть и меняться, например, при изменении атмосферной температуры, при закачке газа или пара в пласт и т. д. Т. о. пористость будет функцией переменных вида: δ = δ (x, y, z, t, p, T_g, T_f). В первом приближении среда считается недеформированной, поэтому функциональная зависимость считается известной.

Тензор коэффициентов проницаемости грунтов.

Обобщенный закон Дарси для анизотропных сред:

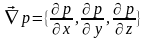,где компоненты вектора скорости фильтрации в прямоугольной декартовой системе координат; -компоненты вектора градиента давления;

- матрица (тензор) коэффициентов проницаемости,

-динамическая вязкость жидкости.

Явный вид этой матрицы зависит от типа анизотропии и системы координат, в которой записан обобщенный закон Дарси. Всегда можно выбрать хотя бы одну систему координат x₁, y₁, z₁ в которой запись обобщенного закона Дарси имеет наиболее простой вид:

Система координат x₁, y₂, z₃, в которой обобщенный закон Дарси имеет простейший вид, называется главной системой координат, а значения k₁, k₂, k₃ - главными значениями тензора проницаемости. Используя запись обобщенного закона Дарси в главной системе координат, можно дать простейшую классификацию эффективной геометрии порового пространства анизотропных сред. Уменьшая число отличных от нуля компонент матрицы коэффициентов проницаемости, можно получить все возможные типы анизотропии и изотропию. Если положить, что все недиагональные элементы матрицы равны нулю, а все диагональные равны друг другу, то получим случай изотропных свойств. Все остальные варианты будут задавать разные типы анизотропии. Матрица коэффициентов проницаемости определяет и задает фильтрационные свойства пористой среды. Матрицы определяют тип свойств – изотропные или анизотропные, а численные значения ее элементов – величины, характеризующие их.

Изотропные фильтрационные свойства задаются матрицей вида - .

Ортотропная матрица - - второй тип анизотропии задает пористую или трещиноватую среду, у которой известны направления всех главных осей, но проницаемости по всем главным направлениям различны. Реальные пористые и трещиноватые среды относятся к след. типам матриц, у которых неизвестно положение главных осей: - неизвестно положение двух главных осей;

3.Физическая скорость движения, скорость фильтрации. Уравнение неразрывности.

Физическая скорость движения, скорость фильтрации.

При движении жидкости в сложном лабиринте пор, как правило, происходит резкое изменение направления и величины физической скорости. Доступными являются средние скорости частицы жидкости в объеме. Введем понятие средней скорости движения по объему пор V₁, которая называется физической скоростью. Понятие средней скорости движения по объему V, которая называется скоростью фильтрации. , используя теорему о среднем , . Физическая скорость всегда больше чем скорость соответствующего фильтрационного потока.

Уравнение неразрывности

Используя понятие скорости фильтрации, запишем через это понятие уравнение неразрывности фильтрационного потока. Выберем в пористой среде некоторый объем V, ограниченный замкнутой поверхностью S. Масса жидкости вытекающей через эту поверхность в единицу времени в результате фильтрации равна . где внешняя нормаль к площадке dS.

Во всем объеме V уменьшение массы жидкости в единицу времени определяется интегралv .

= . В этом случае получим уравнение неразрывности фильтрационного потока в виде дифференциального уравнения: . Перейдем от скорости фильтрации к физической скорости (1.19) Уравнения (1.18) и (1.19) представляют закон сохранения массы фильтрирующейся жидкости, записанный при условии, что объем, занимаемый жидкостью остается неизменным; - определяется из уравнения состояния фильтрирующейся жидкости.