
- •Понятие генеральной совокупности и выборки. Эмпирические аналоги параметров генеральной совокупности. Два взгляда на выборку. Вероятностные свойства выборочных характеристик.
- •Выборочные моменты. Вывести формулы, устанавливающие связь между центральными и начальными выборочными моментами для
- •6. Достаточность точечной оценки. Критерий факторизации. Доказать достаточность средней арифметической , используемой в качестве оценки параметра λ пуассоновского закона распределения .
- •8. Точные и асимптотические законы распределения выборочных характеристик. Вывести закон распределения в предположении, что выборка взята из нормальной генеральной совокупности х.
- •9. Вывести закон распределения ( ) в предположении, что выборки независимы и взяты из нормальных генеральных совокупностей х и у.
- •10. Доказать, что статистика имеет - распределение с (n-1) степенями свободы.
- •11. Доказать, что статистики и s2 , полученные по выборке из нормальной генеральной совокупности, независимы.
- •12. Случайная величина и статистики, имеющие -распределение. Их применение при оценивании параметров и проверке гипотез.
- •13. Случайная величина и статистики, имеющие t-распределение Стьюдента. Их применение в задачах оценивания параметров и проверке гипотез.
- •14. Случайная величина и статистики, имеющие f-распределение, и их применение в математической статистике.
- •16. Интервальные оценки для генеральной дисперсии, полученные по выборке из нормальной генеральной совокупности.
- •19. Проверка гипотез о значении генеральной средней, при известной и неизвестной генеральной дисперсии. Вычисление мощности критерия.
- •20. Проверка гипотез о равенстве генеральных средних двух нормальных генеральных совокупностей. ( это без лекций)
- •21. Проблема Беренса - Фишера. Сравнение математических ожиданий двух нормальных генеральных совокупностей, генеральные дисперсии которых неизвестны и не равны.
- •22. Проверка предположения, что две выборки объемом n1 и n2 взяты из одной нормальной генеральной совокупности.
- •23. Проверка гипотез о значении дисперсии генеральной совокупности. Вычисление мощности критерия (Без вывода мощности)
- •24. Проверка гипотез об однородности дисперсий ряда генеральных совокупностей. Критерии Бартлетта и Кохрана.
- •Проверка гипотезы однородности ряда вероятностей в случае биноминального распределения.
- •Проверка гипотезы однородности ряда вероятностей в случае полиномиального распределения.
- •27.Однофакторный дисперсионный анализ и его цель. Разложение общей вариации на составляющие. Общий вид модели.
- •28.Модель м1 однофакторного дисперсионного анализа. Проверка гипотезы о влиянии фактора а на результативный признак у. Вывести статистику критерия.
- •29. Модель м2 однофакторного дисперсионного анализа. Проверка гипотезы о влиянии фактора а на результативный признак у. Вывести статистику критерия.(нет)
- •30. Модель м1 однофакторного дисперсионного анализа. Проверка гипотезы относительно общего среднего. Вывести статистику критерия.
- •32. Модель м2 однофакторного дисперсионного анализа. Проверка гипотезы относительно общего среднего. Вывести статистику критерия.
- •33. Двухфакторный дисперсионный анализ и его цель. Разложение общей вариации на составляющие. Особенности моделей м1, м2 и смешанных.
Понятие генеральной совокупности и выборки. Эмпирические аналоги параметров генеральной совокупности. Два взгляда на выборку. Вероятностные свойства выборочных характеристик.
Генеральная совокупность – множество всех мыслимых наблюдений, которые могут быть сделаны при данном комплексе условий. Комплекс условий определяет вариацию признака в определенных пределах. Ген. Совокупность – конечная и бесконечная
Выборочная
совокупность
- это мн-во
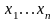 случайно отобранных из ген. совокупности
объектов. Выборка должна быть
репрезентативной – правильно отображать
пропорции ген. сов.т.е каждый элемент
ген. сов. имеет равные шансы попасть в
выборку.
случайно отобранных из ген. совокупности
объектов. Выборка должна быть
репрезентативной – правильно отображать
пропорции ген. сов.т.е каждый элемент
ген. сов. имеет равные шансы попасть в
выборку.
Аналоги:
Распределение
случайной
величины Х
в генеральной совокупности носит
теоретический, идеальный характер, а
ее выборочный аналог является эмпирическим
распределением.
Эмпирическим
распределением называется
распределение, которое каждому элементу
выборки
х1,…,хn ставит
в соответствие p=1/n.
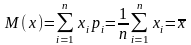 - аналог мат. Ожид
- аналог мат. Ожид
 -
аналог диспр,
-
аналог диспр,
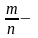 аналог
p,
аналог
p,
![]() - аналог сред.квадр. откл
- аналог сред.квадр. откл
2
взгляда на выборку:
выборка - х1,…,хn
- n-наблюденных
значений СВ, т.е. т чисел. Используется
для расчета
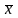 ,
,
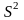 ,
S,
,
S,

выборка
- х1,…,хn –
n-независимых
одинаково распределённых СВ, ЗР которых
совпадает с распределением ген. сов.
 ,
то
,
то
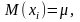 для
любых i=1…n
для
любых i=1…n
 ,
то
,
то
 для любых i=1…n
для любых i=1…n
Вероятностные
свойства выборочных характеристик.
Все
выборочные характеристики (
,
,
S,
)
являются СВ, как функции от СВ
 .
Параметры ген. совокупности
.
Параметры ген. совокупности
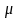 ,
,
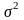 ,
,
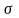 ,
p
- неслучайные
величины и могут быть оценены по выборке.
,
p
- неслучайные
величины и могут быть оценены по выборке.
Выборочные моменты. Вывести формулы, устанавливающие связь между центральными и начальными выборочными моментами для
Выборочные моменты — это оценка теоретических моментов распределения на основе выборки.
Выборочный
момент порядка
![]() —
это СВ,
—
это СВ,
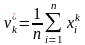 Центральный момент к-порядка:
Центральный момент к-порядка:
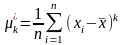
Связи:
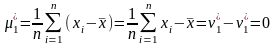
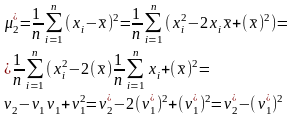


Характеристики ряда распределения. Мода и медиана вариационного ряда. Вывести соотношения между выборочными коэффициентами асимметрии (
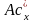 и
и
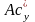 ),
эксцесса (
),
эксцесса (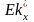 и
и
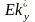 )
и вариации (
)
и вариации (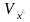 и
и
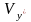 )
случайных величин Х
и Y
, полученных по выборке объёма n,
если
известно, что
)
случайных величин Х
и Y
, полученных по выборке объёма n,
если
известно, что
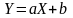 ,
где a
и b
– константы.
,
где a
и b
– константы.
Медиана – значение признака ряда, относительно которого ряд делится на 2 равные по числу признаков части.
1.при
нечетном числе наблюдений n=2l-1
- значению признака Х, приходящегося
на середину ранжированного ряда
наблюдений:
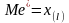 2.при четном числе наблюдений n=2l
–средней арифметической двух значений,
расположенных в середине ранжированного
ряда
2.при четном числе наблюдений n=2l
–средней арифметической двух значений,
расположенных в середине ранжированного
ряда Для интервального ряда медиана
вычисляется по формуле:
Для интервального ряда медиана
вычисляется по формуле: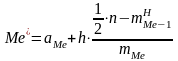
Где h – длина интервала, n – объем выборки
Мода
– значение признака, которому
соответствуют наибольшая частота. Для
одномодального интервального ряда
вычисление моды производится по формуле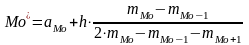
Коэффициент
асимметрии
– показатель асимметричности
распределения, определяющий степень
скошенности кривой по сравнению с
нормальным распределением, и вычисляемый
по формуле:
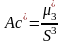 Для
симметричных В.Р. Ас=0, для правосторонней
асимметрии – Ас >0, левосторонней –
Ас<0. Если |Ас|>0,5, то асимметрия
существенна. Коэффициент
эксцесса –
показатель, служащий мерой крутости
(плосковершинности или островершинности)
графику В.Р. в сравнении с кривой
нормального распределения, определяемый
по формуле:
Для
симметричных В.Р. Ас=0, для правосторонней
асимметрии – Ас >0, левосторонней –
Ас<0. Если |Ас|>0,5, то асимметрия
существенна. Коэффициент
эксцесса –
показатель, служащий мерой крутости
(плосковершинности или островершинности)
графику В.Р. в сравнении с кривой
нормального распределения, определяемый
по формуле:
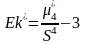 Если Ек>0, то график островершинный,
Ек<0 – плосковершинный. Коэффициент
вариации
–
безразмерный показатель меры рассеяния
значений изучаемого признака и равный
процентному отношению среднего
квадратического отклонения к средней
арифметической:
Если Ек>0, то график островершинный,
Ек<0 – плосковершинный. Коэффициент
вариации
–
безразмерный показатель меры рассеяния
значений изучаемого признака и равный
процентному отношению среднего
квадратического отклонения к средней
арифметической: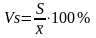 ,
соотношения
для Y=aX+b
,
соотношения
для Y=aX+b
Х
и У:
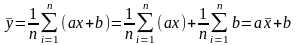 ,
,
 и
и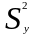 :
:
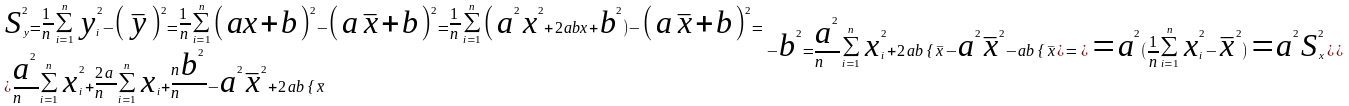
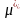 и
и
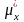 :
: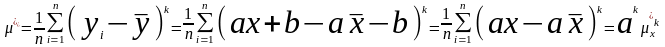
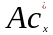 и
и
 :
: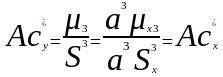
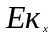 и
и
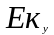 :
:
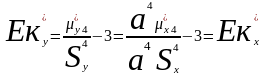
Точечные оценки и их свойства. Проверить оценки математического ожидания и дисперсии нормальной генеральной совокупности ( , S2 и Ŝ2), полученные по выборке
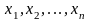 ,
на несмещенность и состоятельность.
,
на несмещенность и состоятельность.
Существует
2 вида оценивания численных значений
параметров ген. сов. – интервальное и
точечное. Точечной
оценкой
 параметра θ называют функцию от
результатов наблюдений
(х1,
х2,…
хn),
значение которой принимают за наилучшее
приближение к оцениваемому параметру
θ.
параметра θ называют функцию от
результатов наблюдений
(х1,
х2,…
хn),
значение которой принимают за наилучшее
приближение к оцениваемому параметру
θ.
Свойства:
Статистическая
оценка
параметра
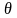 н-ся несмещенной,
если при любой объеме выборки n
её математическое ожидание равно
оцениваемому параметру:
н-ся несмещенной,
если при любой объеме выборки n
её математическое ожидание равно
оцениваемому параметру:
 .Если
оценка является смещенной, то смещение
определяется как
.Если
оценка является смещенной, то смещение
определяется как
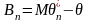 .
Требование несмещенности является
минимальным требованием, т.к. зная
величину смещения, оценку можно всегда
скорректировать.
.
Требование несмещенности является
минимальным требованием, т.к. зная
величину смещения, оценку можно всегда
скорректировать.
Статистическая
оценка
параметра
называется состоятельной,
если она удовлетворяет закону больших
чисел, т.е. при
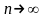 сходится по вероятности к оцениваемому
параметру:
сходится по вероятности к оцениваемому
параметру: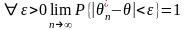 или
или
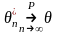 .
.
 >0.
Свойство состоятельности – одно из
главных, т.к. в только в этом случае
имеет смысл увеличивать объем выборки
для повышения точности.
>0.
Свойство состоятельности – одно из
главных, т.к. в только в этом случае
имеет смысл увеличивать объем выборки
для повышения точности.
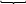
С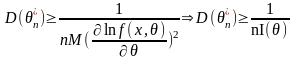 татистическая
оценка
параметра
н-ся эффективной,
если при заданном объеме выборки она
имеет наименьшую возможную дисперсию
среди всех возможных несмещенных
оценок. Эффективность оценки характеризует
средний квадрат отклонения оценки от
оцениваемого параметра
.
татистическая
оценка
параметра
н-ся эффективной,
если при заданном объеме выборки она
имеет наименьшую возможную дисперсию
среди всех возможных несмещенных
оценок. Эффективность оценки характеризует
средний квадрат отклонения оценки от
оцениваемого параметра
.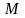 (
( -
-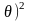 При
этом, согласно неравенству Рао-Камера,
дисперсия любой несмещенной оценки
параметра
ограничена снизу:
При
этом, согласно неравенству Рао-Камера,
дисперсия любой несмещенной оценки
параметра
ограничена снизу: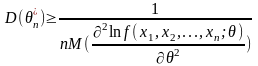 ,где
,где
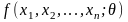 -
плотность. Эффективность оценки
определяется отношением
-
плотность. Эффективность оценки
определяется отношением
 )=
)=
Статистическая
оценка
параметра
называется достаточной,
если условное распределение
 не зависит от
для всех возможных значений
,
содержит всю информацию об оцениваемом
параметре. Достаточность определяют
с помощью критерия факторизации, когда
функция правдоподобия L(Х1,…,Хn/
)
может быть представлена в виде
произведений двух сомножителей: 1-й
зависит от
и
,а
2-й от результатов наблюдения
.
То есть L(Х1,…,Хn/
)
= G (
;
)
* Н(Х1,…,Хn). Эффективная оценка является
и достаточной.
не зависит от
для всех возможных значений
,
содержит всю информацию об оцениваемом
параметре. Достаточность определяют
с помощью критерия факторизации, когда
функция правдоподобия L(Х1,…,Хn/
)
может быть представлена в виде
произведений двух сомножителей: 1-й
зависит от
и
,а
2-й от результатов наблюдения
.
То есть L(Х1,…,Хn/
)
= G (
;
)
* Н(Х1,…,Хn). Эффективная оценка является
и достаточной.
 ,
,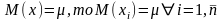

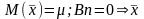 несмещенная
оценка
,
несмещенная
оценка
,
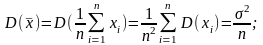 Bn=0
=> оценка несмещенная
Bn=0
=> оценка несмещенная
оценка состоятельности:
1)Bn=0,
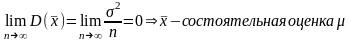

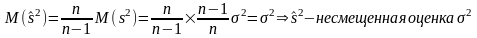

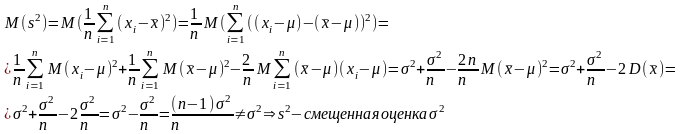
5. Эффективность и асимптотическая эффективность точечной оценки. Неравенство Рао-Крамера. Доказать, что средняя арифметическая , полученная по результатам выборки из генеральной совокупности, имеющей экспоненциальный закон распределения с плотностью:
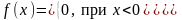
является эффективной оценкой параметра λ.
Точечная оценка – некоторая ф-ия результатов наблюдений (х1…хn), значение которой принимают за наилучшее приближение в данных условиях к значению параметра Q ген. Совокупности Х.Статистическая оценка параметра н-ся эффективной, если при заданном объеме выборки она имеет наименьшую возможную дисперсию среди всех возможных несмещенных оценок. Эффективность оценки характеризует средний квадрат отклонения оценки от оцениваемого параметра . ( - .
Неравенство Рао-Крамера ограничивает дисперсию любой несмещенной оценки параметра Q снизу:
.
Количество информации Фишера о параметре Q,содержащейся в единичном наблюдении
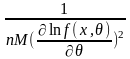 =
=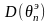 .
Эффективность параметра определяется
соотношением
.
Эффективность параметра определяется
соотношением
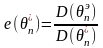 .
.
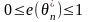 Если
Если
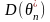 совпадает
с нижней границей, то оценка
эффективна.Однако существование
эффективной оценки это довольно сильное
требование на задачу. Более слабым
является условие асимптотической
эффективности,
которое означает, что отношение дисперсии
несмещенной оценки к нижней границе
Крамера-Рао стремится к единице при
совпадает
с нижней границей, то оценка
эффективна.Однако существование
эффективной оценки это довольно сильное
требование на задачу. Более слабым
является условие асимптотической
эффективности,
которое означает, что отношение дисперсии
несмещенной оценки к нижней границе
Крамера-Рао стремится к единице при
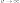 ,т.е.
,т.е.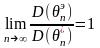 Решение
Решение
 =x
ср
=x
ср
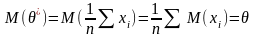 =>
несмещенная
=>
несмещенная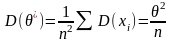 ,
,
 =>
состоятельная
=>
состоятельная
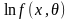 =
=
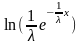 =
=
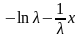
 =
=
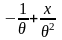 , I
= M
(
)
, I
= M
(
)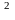 =M
(
=M
(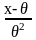 )
=
)
=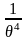 M(x-
)
=
M(x-
)
= =
=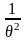
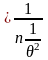 =
=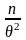 .
.
т.к.
 ,то оценка эффективна. Эффективная
оценка является и достаточной
,то оценка эффективна. Эффективная
оценка является и достаточной
