6 Вопрос

Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.

Примером такого движения является движение тела, брошенного под углом   к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением  , направленным вертикально вниз.

При равноускоренном движении по прямой скорость тела определяется формулой:

Зная, что  , найдём формулу для определения координаты x:

Примечание. Равнозамедленным можно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора   и   противонаправлены). Равнозамедленное движение также является равноускоренным.

Перемещение в случае одномерного равноускоренного движения

В случае одномерного равноускоренного движения вдоль координаты x имеет место формула:

,

Скорость

Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор г₀ (рис. 3). В течение малого промежутка времени t точка пройдет путь s и получит элементарное (бесконечно малое) перемещение г.

Вектором средней скорости <v> называется отношение приращения г радиуса-вектора точки к промежутку времени t:

(2.1)

Направление вектора средней скорости совпадает с направлением г. При неограниченном уменьшении t средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v:

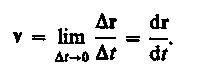
Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения t путь s все больше будет приближаться к |г|, поэтому модуль мгновенной скорости

Таким образом, модуль мгновенной скорости равен первой производной пути по времени:

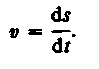(2.2)

При неравномерном движении модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной <v> — средней скоростью неравномерного движения:

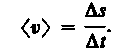
Из рис. 3 вытекает, что <v> > |<r>|, так как s >|г|, и только в случае прямолинейного движения

Если выражение ds=vdt (см. формулу (2.2)) проинтегрировать по времени в пределах от t до t+t, то найдем длину пути, пройденного точкой за время t:

(2.3)

В случае равномерного движения числовое значение мгновенной скорости постоянно; тогда выражение (2.3) примет вид

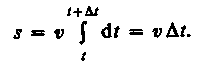
Длина пути, пройденного точкой за промежуток времени от t\ до fa, дается интегралом

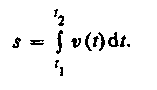
Ускорение и его составляющие

Ускорение – характеризует быстроту изменения скорости по величине и направлению.

- полное ускорение = геометрической сумме (векторной) нормального и тангенсуального ускорения. =а +а

Рассмотрим плоское движение, т. е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор v задает скорость точки А в момент времени t. За время t движущаяся точка перешла в положение В и приобрела скорость, отличную от v как по модулю, так и направлению и равную v₁ = v + v. Перенесем вектор v₁ в точку А и найдем v (рис. 4).

Рис. 4

Средним ускорением неравномерного движения в интервале от t до t+r называется векторная величина, равная отношению изменения скорости Ду к интервалу времени г:

Мгиовеивым ускорением а (ускорением) материальной точки в момент време ни t будет предел среднего ускорения:

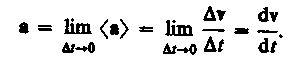
Таким образом, ускорение а есть векторная величина, равная первой производной скорости по времени.

Разложим вектор v на две составляющие. Для этого из точки А (рис. 4) по направлению скорости v отложим вектор , по модулю равный v₁. Очевидно, что вектор , равный v_, определяет изменение скорости за время t по модулю: v_ = v₁ - v. Вторая же составляющая v_n вектора v характеризует изменение скорости за время t по направлению.

Тангенциальная составляющая ускорения – составляющая полного ускорения тела криволинейного движения материальной точки, которая характеризует численное изменение скорости и направленно по касательной в сторону отправления движения.

- нормальное и тангенсуальное ускорение взаимоперпендикулярны.

т. е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

Найдем вторую составляющую ускорения. Допустим, что точка В достаточно близка к точке А, поэтому s можно считать дугой окружности некоторого радиуса г, мало отличающейся от хорды АВ. Тогда из подобия треугольников АОВ и EAD следует , но так как AB=vt, то

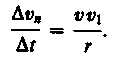В пределе при t  0 получим v₁  v.

Поскольку v₁ = v, угол EAD стремится к нулю, а так как треугольник EAD равнобедренный, то угол ADE между v и v_n стремится к прямому. Следовательно, при t  0 векторы v_n и v оказываются взаимно перпендикулярными. Так как вектор скорости направлен по касательной к траектории, то вектор v_n, перпендикулярный вектору скорости, направлен к центру ее кривизны. Вторая составляющая ускорения, равная

называется нормальной составляющей ускорения (составляющая полного ускорения тела (центростремительного) криволинейного движения материальной точки, которая характеризует быстроту изменения скорости по направлению и направлена по главной нормали траектории движения в сторону центра кривизны) поэтому ее называют также центростремительным ускорением). Полное ускорение тела есть геометрическая сумма тангенциальной и нормальной составляющих (рис. 5):

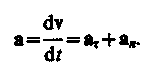
Формула пути при равномерном движении.. Скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела к промежутку времени, в течение которого было совершено это перемещение:  v=s/t.

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

.

Записав аналогичные соотношения для координат y и z и просуммировав все три равенства получим соотношение:

.

Слева стоит работа постоянной равнодействующей силы  , а справа — разность кинетических энергий в конечный и начальный момент движения.

22.Ламинарное и турбулентное течения жидкости. Число рейнольдса. Уравнение неразрывности для несжимаемой жидкости.

Ламина́рное тече́ние (лат. lāmina — «пластинка») — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления). Только в ламинарном режиме возможно получение точных решений уравнения движения жидкости (уравнений Навье-Стокса), например течение Пуазейля.

ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ (от латинского turbulentus - бурный, беспорядочный), течение жидкости или газа, при котором частицы жидкости совершают неупорядоченные, хаотические движения по сложным траекториям, а скорость, температура, давление и плотность среды испытывают хаотические флуктуации. Отличается от ламинарного течения интенсивным перемешиванием, теплообменом, большими значениями коэффициент трения и пр. В природе и технике большинство течений жидкости и газов - турбулентные течения.

Турбулентное течение отличаются от соответствующих ламинарных течений как своей сложной внутренней структурой (рис. 1), так и распределением осреднённой скорости по сечению потока и интегральными характеристиками — зависимостью средней по сечению или максимальной скорости, расхода, а также коэффициента сопротивления от Рейнольдса числа Re.

Число, или, правильнее, критерий Рейно́льдса (), — безразмерная величина, характеризующая отношение нелинейного и диссипативного членов в уравнении Навье-Стокса^[1]. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса определяется следующим соотношением:

где

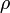• — плотность среды, кг/м³;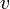

• — характерная скорость, м/с;

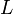• — характерный размер, м;

• — динамическая вязкость среды, Н·с/м²;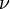

• — кинематическая вязкость среды, м²/с( ) ;

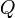• — объёмная скорость потока;

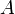• — площадь сечения трубы.

Уравнение неразрывности для несжимаемой жидкости

Sv = const

• где S - площадь поперечного сечения трубки тока жидкости; v - скорость течения жидкости.

23.Реальная и идеальная жидкость. Уравнение Бернули и следствия из него. Статическое давление. Динамическое давление. Гидростатическое давление полное давление

Идеа́льная жи́дкость — в гидродинамике — воображаемая (идеализированная) жидкость, в которой, в отличие от реальной жидкости, отсутствуетвязкость . В идеальной жидкости отсутствует внутреннее трение, то есть нет касательных напряжений между двумя соседними слоями.

Реальная, или действительная, жидкость не обладает в совершенстве свойствами идеальной жидкости, она в некоторой степени сопротивляется касательным и растягивающим усилиям, а также отчасти сжимается. Для решения многих задач гидравлики этим отличнем в свойствах идеальной и реальной жидкостей можно пренебречь. В связи с этим законы, выведенные для идеальной жидкости, могут быть применены к жидкостям реальным с соответствующими поправками, а иногда даже без них.

Уравнение Бернулли для стационарного течения идеальной не­сжимаемой жидкости

ρv² / 2 + ρgh + p  = const

 где Р - статическое давление жидкости для определенного сечения труб­ки тока; v -скорость жидкости для этого же сечения; h -высота, на ко­торой расположено сечение.

Динамическое давление связано с движением жидкости и проявляется в том случае, если жидкость при встрече с препятствием теряет скорость (v ->0).

Статическое давление — это давление неподвижной жидкости. Статическое давление = уровень выше соответствующей точки измерения + начальное давление в расширительном баке.

Динамическое давление — это давление движущегося потока жидкости.

Гидростатическое давление - давление столба воды над условным уровнем. Измеряется высотой столба воды в единицах длины или в атмосферах

Полное давление- давление p0 изоэнтропически заторможенной жидкости или газа.

24.Формула Торричелли для определения скорости потока жидкости

Формула Торричелли — это формула, позволяющая найти конечную скорость тела, движущегося с постоянным ускорением, если не известно время движения.

Формула выглядит следующим образом:

Получена Эванджелиста Торричелли.