3.5 Плоскость в пространстве. Нормальное уравнение плоскости
Пусть в трехмерном пространстве задана прямоугольная декартова система координат.
Общим уравнением плоскости в пространстве называется уравнение вида
Ax + By + Cz + D = 0, |
где A2 + B2 + C2 ≠ 0 .
В трехмерном пространстве в декартовой системе координат любая плоскость описывается уравнением 1–ой степени (линейным уравнением). И обратно, любое линейное уравнение определяет плоскость
Нормальное уравнение плоскости
где 
-
углы, образуемые нормальным вектором
плоскости с осями координат; p -
расстояние от начала координат до
плоскости.
Приведение общего уравнения плоскости к нормальному виду:
Здесь 
-
нормирующий множитель плоскости, знак
которого выбирается противоположным
знаку D,
если 
произвольно,
если D
= 0.
3.6 Общим уравнением плоскости в пространстве называется уравнение вида
Ax + By + Cz + D = 0, |
где A2 + B2 + C2 ≠ 0 .
В трехмерном пространстве в декартовой системе координат любая плоскость описывается уравнением 1–ой степени (линейным уравнением). И обратно, любое линейное уравнение определяет плоскость
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
3.7 Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть в трехмерном пространстве задана прямоугольная декартова система координат. Сформулируем следующую задачу:
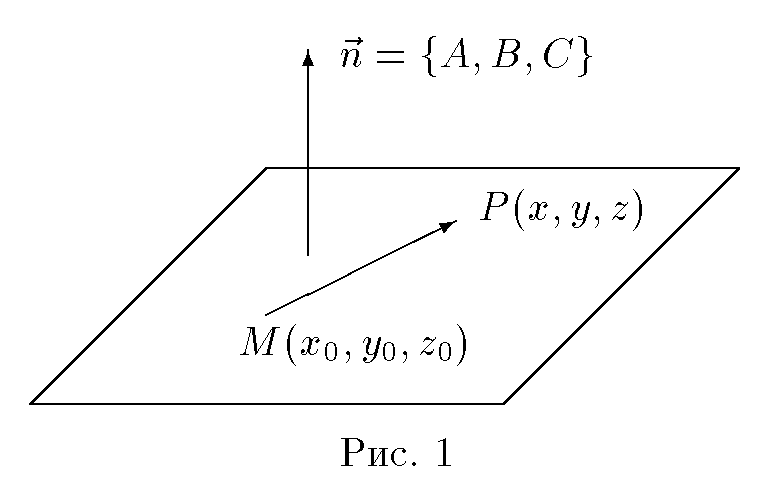
Составить уравнение плоскости, проходящей через данную точку M(x0, y0, z0) перпендикулярно данному вектору
→ |
n |
= {A, B, C} .
Решение. Пусть P(x, y, z) — произвольная точка пространства. Точка P принадлежит плоскости тогда и только тогда, когда вектор MP = {x − x0, y − y0, z − z0} ортогонален вектору
→ |
n |
= {A, B, C} (рис.1).
Написав условие ортогональности этих векторов (
→ |
n |
, MP) = 0 в координатной форме, получим:
|
A(x − x0) + B(y − y0) + C(z − z0) = 0 |
(1) |
Это и есть искомое уравнение. Вектор
→ |
n |
= {A, B, C} называется нормальным вектором плоскости.
Таким образом, чтобы написать уравнение плоскости, нужно знать нормальный вектор плоскости и какую–нибудь точку, принаждежащую плоскости.
Если теперь в уравнении (1) раскрыть скобки и привести подобные члены, получим общее уравнение плоскости:
Ax + By + Cz + D = 0 , |
где D = −Ax0 − By0 − Cz0 .
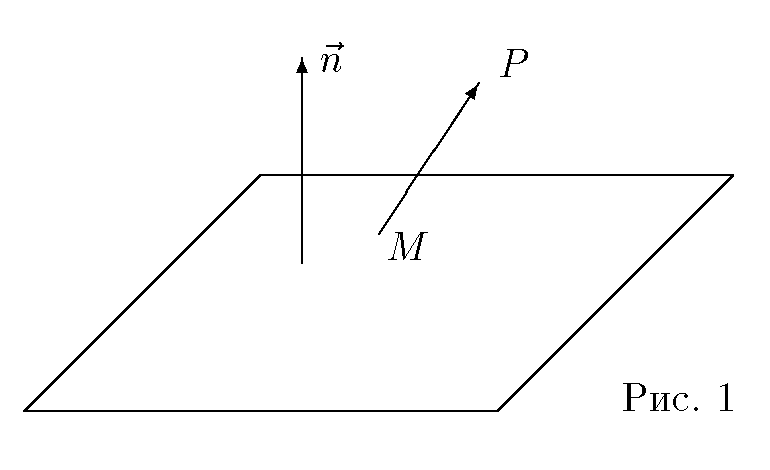
3.8 Найти расстояние d от точки P(x0, y0, z0) до плоскости Ax + By + Cz + D = 0 .
Решение.Фиксируем некоторую точку M(x1, y1, z1), , принадлежащую плоскости, и построим вектор MP (рис. 1).
→ |
n |
. Получаем
|
|
(1) |
В нашем случае
→ |
n |
= {A, B, C} и MP = {x0 − x1, y0 − y1, z0 − z1} .
По формуле (1)
d = |
|
√
|
|
. |
|||
|
|
|