3 14 Пересечение прямой с плоскостью.

Если прямая не лежит в плоскости и не параллельна ей, она пересекает плоскость. Задача на определение точки пересечения прямой с плоскостью сводится к следующему: 1) проведению вспомогательной плоскости (Вспомогательную плоскость рекомендуется выбирать такую, которая даст наиболее простое графическое решение задачи) через данную прямую; 2) нахождению линии пересечения вспомогательной плоскости с данной плоскостью; 3) определению точки пересечения данной прямой с линией пересечения плоскостей, а следовательно, с данной плоскостью.

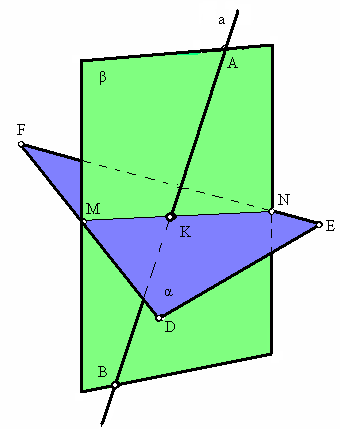
Пример построения точки пересечения (К) прямой а (АВ) с плоскостью α (DEF) показан на рис. 3.10. Для этого прямая а заключена в произвольную плоскость β и определена линия пересечения плоскостей α и β.

В рассматриваемом примере прямые АВ и MN принадлежат одной плоскости β и пересекаются в точке К, а так как прямая MN принадлежит заданной плоскости α (DEF), то точка К является и точкой пересечения прямой а (АВ) с плоскостью α. (рис. 3.11).

.

Рис. 3.10. Построение точки пересечения прямой с плоскостью

Для решения подобной задачи на комплексном чертеже необходимо уметь находить точку пересечения прямой общего положения с плоскостью общего положения.

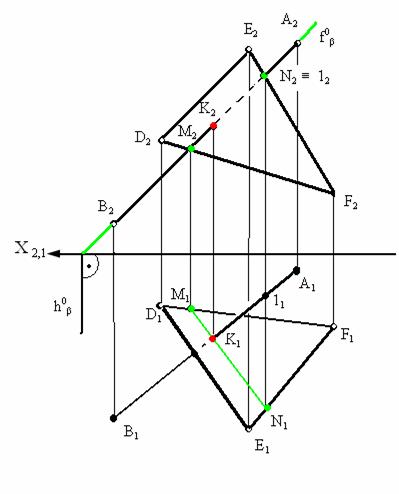
Рассмотрим пример нахождения точки пересечения прямой АВ c плоскостью треугольника DEF представленный на рис. 3.11.

Для нахождения точки пересечения через фронтальную проекцию прямой А₂В₂ проведена фронтально-проецирующая плоскость β которая пересекла треугольник в точках M и N. На фронтальной плоскости проекций (π₂) эти точки представлены проекциями M₂, N₂. Из условия принадлежности прямой плоскости на горизонтальной плоскости проекций (π₁) находятся горизонтальные проекции полученных точек M₁ N₁. В пересечении горизонтальных проекций прямых А₁В₁ и M₁N₁ образуется горизонтальная проекция точки их пересечения (К₁). По линии связи и условиям принадлежности на фронтальной плоскости проекций находится фронтальная проекция точки пересечения (К₂).

.

Пример определения точки пересечения прямой и плоскости

Видимость отрезка АВ относительно треугольника DEF определена методом конкурирующих точек.

На плоскости π₂ рассмотрены две точки N EF и 1 АВ. По горизонтальным проекциям этих точек можно установить, что точка N расположена ближе к наблюдателю (Y_N>Y₁ ), чем точка 1 (направление луча зрения параллельно S). Следовательно, прямая АВ, т. е. часть прямой АВ (К₁) закрыта плоскостью DEF на плоскости π₂ (ее проекция К₂1₂ показана штриховой линии). Аналогично установлена видимость на плоскости π₁.

3.15 Преобразования параллельного переноса и поворота системы координат. Упрощение уравнений кривых

Иногда при решении задач удобно вместо данной системы XOY использовать другую X'O'Y', определенным образом ориентированную относительно данной системы.

Пусть новая система X'O'Y' получена из старой ХОY параллель-ным переносом осей координат, т.е. оси новой системы параллельны осям старой и имеют одинаковое с ними направление (рис. 4.4). Пусть начало О' новой системы имеет координаты (a, b) в старой системе.

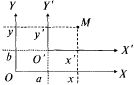
Рис. 4.4

Возьмем т. М на плоскости и найдем зависимость между ее координатами (х, у) в старой системе и (х', у') в новой. Из рис. 4.4 ясно, что

Если уравнение кр. 2п (4.1) не содержит члена с произведением координат (В= 0), то с помощью параллельного переноса оно приводится к каноническому виду. Для этого необходимо в случае выделить полные квадраты для членов, содержащих у, и членов, содержащих х, затем для полученных полных квадратов вида

обозначить через новые переменные х' = х - а, у' =у - b.

Пример:

Введем новые переменные и новое начало координат O'(1, -2). Тогда, разделив обе части уравнения на 4, получим каноническое уравнение гиперболы  действительная полуось мнимая b = 2. Построим эту гиперболу в системе координат X'O'Y' (рис. 4.5)

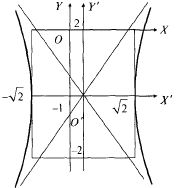
Рис. 4.5

Если В 0 в общем уравнении кр. 2п (4.1), то первые три слагаемых образуют квадратичную форму от двух переменных

Приводя ее к каноническому виду, получим  где — собственные значения матрицы Р,х',у' — новые ко-

ординаты в системе Х'О'Y.

Пусть — старый ортонормированный базис, — но-

вый. Выразим формулы преобразования координат через угол  отсчитываемый в направлении кратчайшего поворота от

 к Имеем (рис. 4.6)

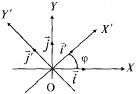
Рис. 4.6

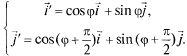
Следовательно, формулы преобразования координат, которые называются преобразованием поворота системы координат на угол запишутся в виде:

Подставляя их в общее уравнение кр. 2п, получим уравнение, не содержащее слагаемого с произведением ху, затем применяем преобразование параллельного переноса.

3.16 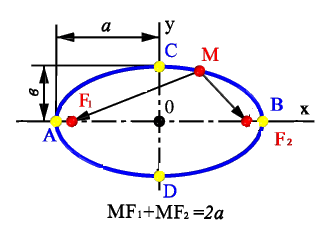         Обозначим фокусы эллипса буквами   и  . Расстояние между ними - фокальное расстояние  ,  и  . Если   - произвольная точка эллипса, то по определению эллипса   - характеристическое уравнение эллипса .

        Введем систему координат:  ,   и  . Тогда фокусами будут точки  и  .

        Пусть   - любая точка эллипса, тогда

 

        Запишем характеристическое уравнение эллипса в координатной форме:

        Преобразуем равенство:

        Перенесем в левую часть равенства выражение, содержащее корень:

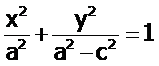
        Так как  , то  . Пусть  , то

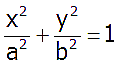 - каноническое уравнение эллипса .

 Эллипсом называется геометрическое место точек, для которых сумма расстояний до двух фиксированных точек (фокусов) есть для всех точек эллипса одна и та же постоянная величина (эта постоянная величина должна быть больше, чем расстояние между фокусами).

Простейшее уравнение эллипса

где a - большая полуось эллипса, b - малая полуось эллипса. Если 2c - расстояние между фокусами, то между a, b и c (если a > b) существует соотношение

a² - b² = c².

Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси

У эллипса эксцентриситет e < 1 (так как c < a), а его фокусы лежат на большой оси.