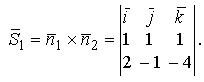3.9 Угол между плоскостями. Перпендикулярность плоскостей

Пусть плоскости α и β пересекаются по прямой с.  Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

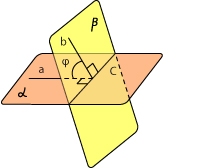
Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.

Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны,

Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:

Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

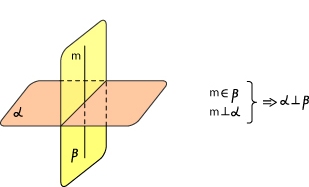
Две плоскости называются параллельными, если они не имеют общих точек.

Свойства и признаки

• Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны

• Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны

• Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну

• Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны

• Два угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях

3.10

Каноническое уравнение прямой в пространстве

Если известны координаты точки A(x₀, y₀, z₀) лежащей на прямой и направляющего вектора n= {l;m; n}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

- каноническое уравнение прямой в пространстве

Каноническое уравнение прямой на плоскости

Если известны координаты точки A(x₀, y₀) лежащей на прямой и направляющего вектора n = {l;m}

, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x- x0	=	y- y0
l		m

3.11

Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

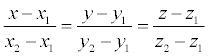
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:

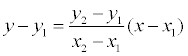
если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь 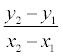 = k называется угловым коэффициентом прямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Решение. Применяя записанную выше формулу, получаем:

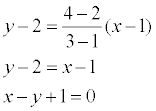
3.12 Общие уравнения прямой в пространстве

Линия в трехмерном пространстве определяется, вообще говоря, пересечением двух поверхностей, т.е. описывается системой двух уравнений.

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей и, следовательно, описывать системой двух линейных уравнений

	  	A1x + B1y + C1z + D1 = 0 A2x + B2y + C2z + D2 = 0

при условии, что эти плоскости непараллельны, т.е. их нормальные векторы 

→

n

₁ = {A₁, B₁, C₁} и 

→

n

₂ = {A₂, B₂, C₂} неколлинеарны. Эта система уравнений называется общими уравнениями прямой в пространстве.

Пример 1. Уравнение прямой задано в общем виде

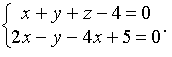
Необходимо записать уравнение прямой в каноническом виде.

Решение. Для записи уравнений (14) нам нужно знать координаты какой-либо точки M₀на прямой и координаты какого-либо направляющего вектора   прямой. Находим координаты точки M₀(x₀, y₀, z₀). Для этого одну из координат задаем произвольно (так, чтобы оставшаяся система двух уравнений с двумя неизвестными имела единственное решение), скажем, z₀ = 0. После этого решаем систему относительно x₀ и y₀

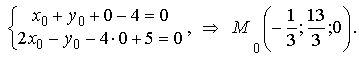
Для определения вектора   нам нужны координаты еще одной точки M₁ на прямой (рис. 3), тогда в качестве направляющего вектора можно взять вектор 

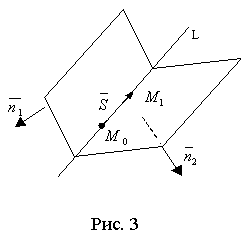
Для вычисления координат M₁ берем, например z₁ = 1, а x₁и y₁ находим из решения системы

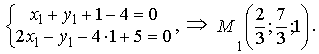
Тогда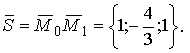 

Канонические уравнения прямой имеют вид

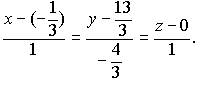
Один из направляющих векторов можно было найти и как векторное произведение нормальных векторов плоскостей, то есть