3.13 Вычисление угла между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости

Рассмотрим прямую l с направляющим вектором а и плоскость р с нормальным вектором п. Обозначим через φ угол между прямой l и плоскостью р, а через ψ — угол между векторами а и n. Легко видеть, что φ  = 90° — ψ , если ψ < 90° (рис. 209, а) и φ = ψ — 90°, если ψ > 90° (рис. 209,6).

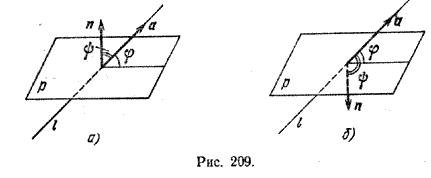
В обоих случаях справедливо равенство sin φ = | cos ψ) |.

По формуле (1) § 20 находим

и, следовательно,

Если известны прямоугольные декартовы координаты направляющего вектора прямой и нормального вектора плоскости a = (a₁; a₂; a₃) и n = (А; В; С), то угол φ может быть вычислен с помощью формулы

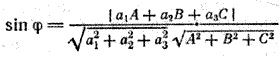        (1)

Задача 1. Вычислить угол между прямой и плоскостью:

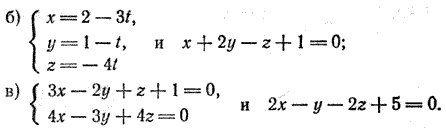
а) В данном случае a = (2; 2; —1), n = (4; 1; 1). По формуле (1) вычисляем синус искомого угла:

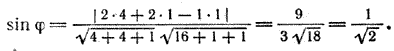
Угол между прямой и плоскостью равен 45°.

б) Так как а = (—3; —1; —4) и n = (1; 2; —1), то

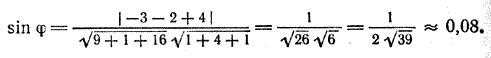
По таблице синусов находим, что φ ≈  5°.

в) За направляющий вектор прямой возьмем векторное произведение нормальных векторов n₁ = (3; —2; 1) и n₂ = (4; —3; 4) плоскостей, задающих прямую. Найдем его координаты:

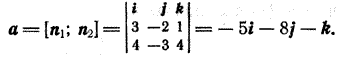
Координаты нормального вектора данной плоскости находим из ее уравнения  n = (2; —1; —2). По формуле (1) вычисляем синус искомого угла:

Угол между прямой и плоскостью равен нулю.

Прямая с направляющим вектором а и плоскость с нормальным вектором ппараллельны тогда и только тогда, когда векторы а и n перпендикулярны (рис. 210,а). Для перпендикулярности прямой и плоскости, очевидно, необходимо и достаточно, чтобы векторы  а и n   были коллинеарны (рис. 210, б).

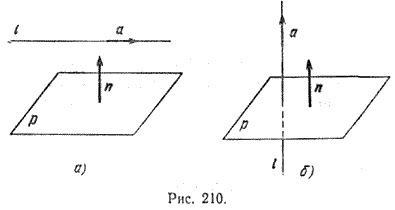
Если прямая и плоскость заданы уравнениями

то они:

а) параллельны тогда и только тогда, когда

а₁А + а₂В + а₃С = 0;       (2)

б) перпендикулярны тогда и только тогда, когда

     (3)

Прямая лежит в плоскости тогда и только тогда, когда она, во-первых, параллельна плоcкости и, во-вторых, хотя бы одна ее точка принадлежит плоскости. Поэтому необходимое и достаточное условие принадлежности прямой   плоскости Ах +Ву + Сz + D = 0 заключается в выполнении следующих двух равенств:

а₁А + а₂В + а₃С  = 0   и   Ах₁ +Ву₁ + Сz₁ + D = 0.   (4)

Задача 2. Среди следующих пар прямых и плоскостей указать параллельные или перпендикулярные; в случае пересечения прямой и плоскости найти точку пересечения:

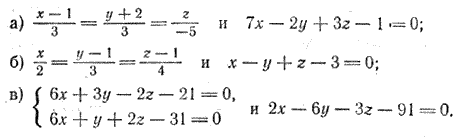
а) Направляющий вектор прямой имеет координаты a = (3; 3; —5), нормальный вектор плоскости —   n = (7; —2; 3). Векторы, очевидно, не коллинеарны; следовательно, прямая не перпендикулярна плоскости. Проверим условие (2) параллельности прямой и плоскости:

а₁А + а₂В + а₃С = 3 • 7 — 3 • 2 — 5 • 3 = 0.

Условие выполняется. Данные прямая и плоскость параллельны.

б) В данном случае а = (2; 3; 4) и п = (1; —1; 1). Векторы не коллинеарны, поэтому условие (3) не выполняется. Проверим условие (2) параллельности прямой и плоскости:

а₁А + а₂В + а₃С = 2 • 1 — 3 • 1 + 4 • 1 =/= 0.

Условие не выполняется. Прямая и плоскость не параллельны и, следовательно, пересекаются. Для определения координат точки пересечения нужно решить систему трех уравнений с тремя неизвестными:

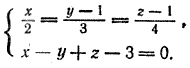
Такую систему удобно решать, предварительно записав уравнения прямой в параметрическом виде:

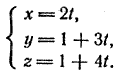
Подставляя значения х, у и z в уравнение плоскости, получим

2t —  (1 + 3t) + 1 + 4t — 3 = 0,

откуда t = 1 и, значит, х = 2, у = 4, z = 5. Прямая и плоскость пересекаются в точке  (2; 4; 5).

в) За направляющий вектор прямой возьмем векторное произведение векторов  n₁=(6; 3;—2) и п₂ =  (6; 1; 2), т. е. нормальных векторов, задающих данную прямую. Найдем его координаты:

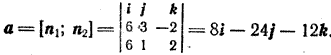
Нормальный вектор п данной плоскости имеет координаты (2; —6; —3). Условие (3)   перпендикулярности прямой и плоскости выполнено, так как

⁸/₂ =   ^—24/_—6 = ^—12/_—3

Данные прямая и плоскость перпендикулярны. Для определения точки пересечения прямой и плоскости запишем уравнения прямой в параметрическом виде. Направляющий вектор прямой уже найден, это вектор а =  (8; —24; —12) или ему коллинеарный вектор (2; —6; —3). Осталось найти какую-нибудь точку прямой. Положим х = 0, тогда

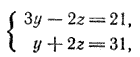
откуда у = 13, z = 9. Точка (0; 13; 9) принадлежит прямой. Следовательно, параметрические уравнения прямой имеют вид

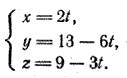
Подставляя значения х, у и z в уравнение плоскости, получим

4t — 6(13 — 6t) — 3 (9 — 3t) — 91 = 0

или 49t = 196, t = 4. Точка прямой, получающаяся при значении параметра t = 4, принадлежит плоскости. Прямая и плоскость пересекаются в точке (8; —11; —3).