Пример 7.1

Исследовать систему уравнений. В случае совместности решить

Ответ: Система совместна и имеет бесконечное множество решений вида:

, , где

Пример 7.2

Исследовать систему

Ответ: Система несовместна (нет решений)

Пример 7.3

Исследовать и решить систему уравнений.

Ответ: Система совместна и имеет единственное решение , ,

§8. Метод Гаусса.

Рассмотрим систему m линейных уравнений с n неизвестными.

Матрицу системы и расширенную матрицу с помощью элементарных преобразований можно свести или к треугольному виду или к ступенчатому виду.

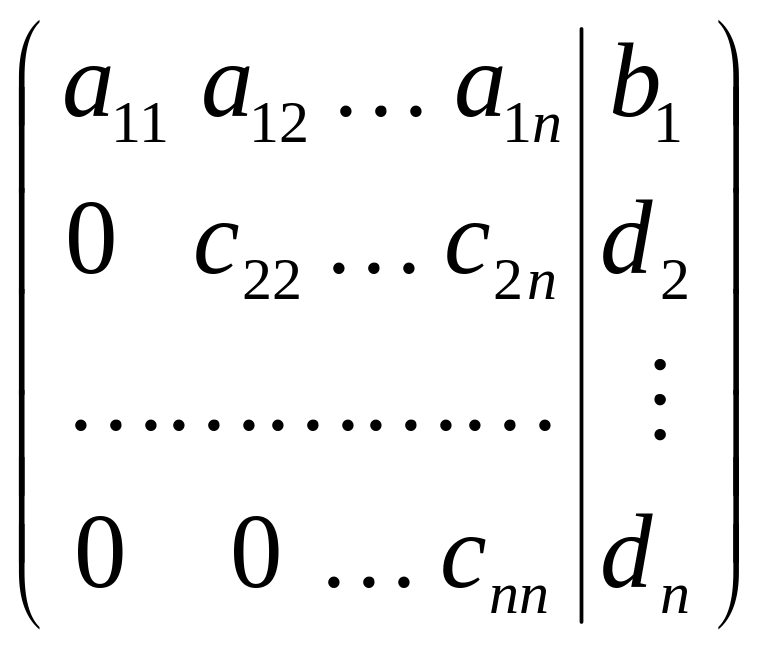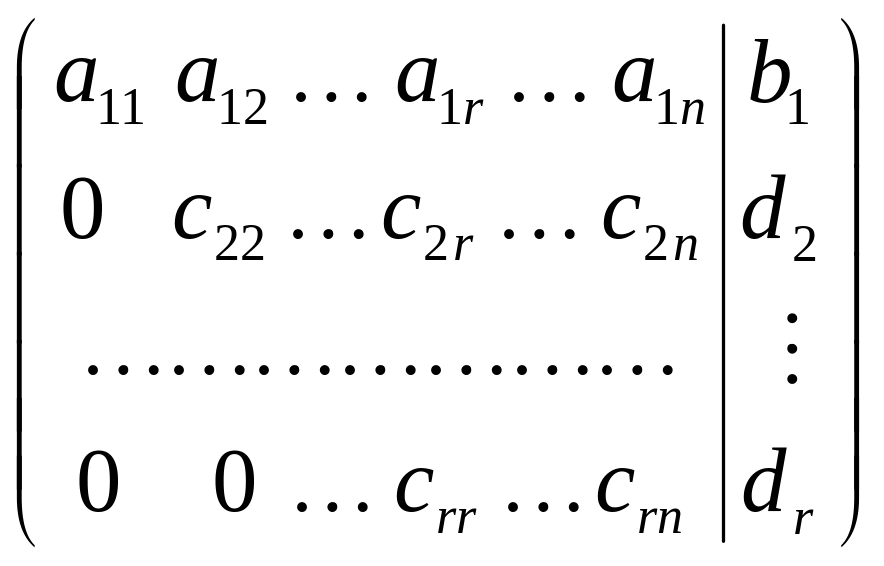(1) (2)

Матрице (1) соответствует система:

Если а₁₁, с₂₂, …с_nn 0, то начиная с последнего уравнения найти единственное

решение x_n, x_n-1,…,x₁.

Если условие а₁₁, …, с_nn 0 не выполняется, то переставить столбцы.

Матрице (2) соответствует система:

Если a₁₁, c₂₂,…,c_rr 0, то r(A)= r( ) =r<n бесконечное множество решений.

r базисных неизвестных: x₁, x₂,…,x_r, где

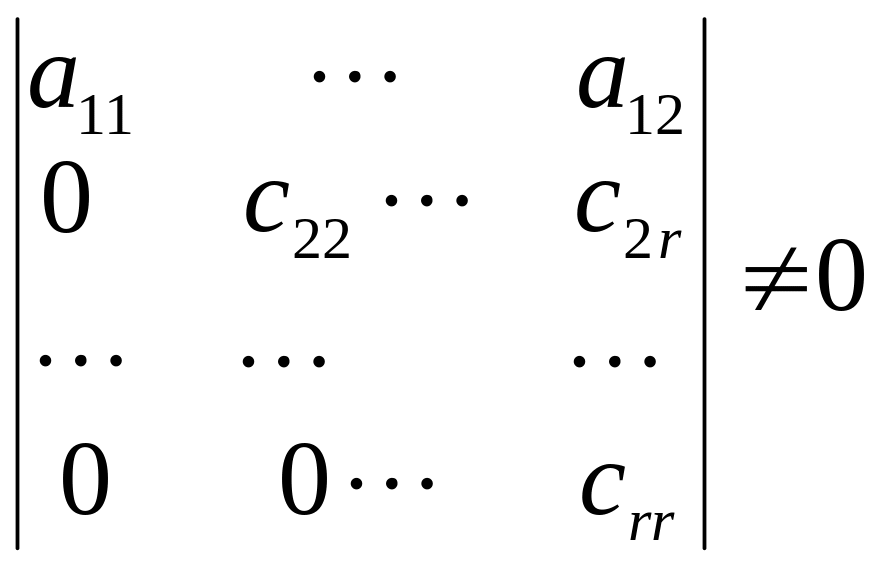
(n-r) свободных неизвестных: x_r+1, …, x_n

Выразить x₁,…,x_r через x_r+1,…,x_n.

Замечание. Если в матрице (1) или (2) есть такая i–я строка, у которой все

c_ij=0, а d_i0 (противоречивое уравнение), то система несовместна, так как r(A) r( ).

Данный метод называется методом Гаусса.

Метод Гаусса позволяет решить систему и исследовать ее на совместность.

Пример 8.1

Решить систему методом Гаусса.

Ответ: , ,

§9. Однородные системы уравнений.

Рассмотрим однородную систему уравнений.

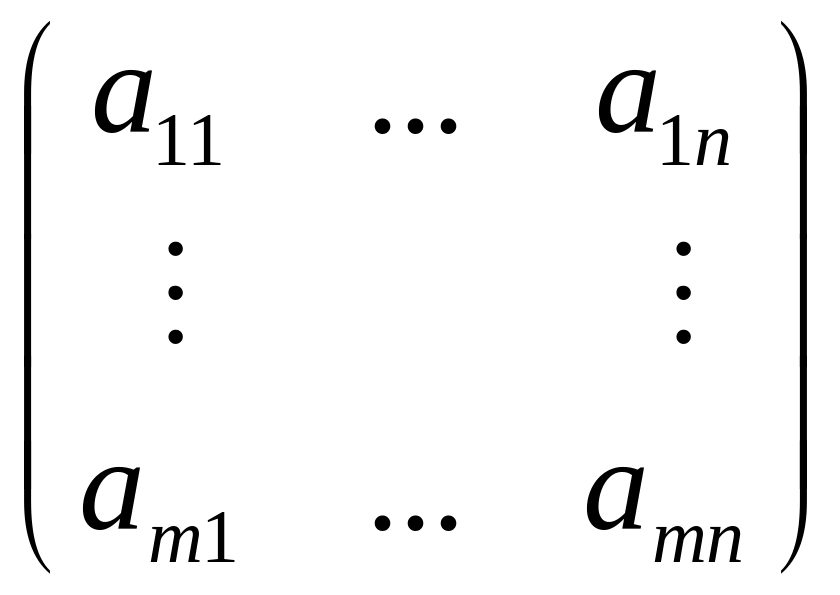В матричном виде: , где А= ; Х= .

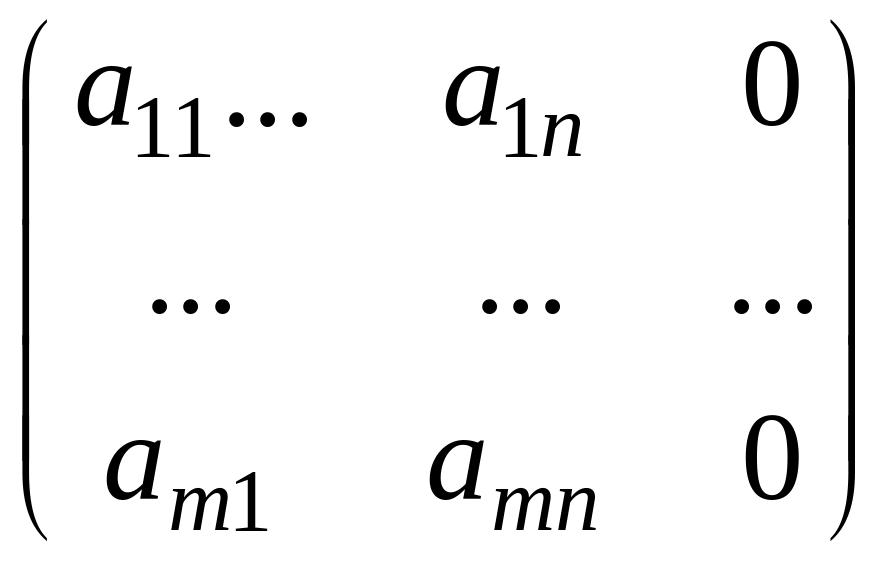– расширенная матрица

А~ (вычеркнув нулевой столбец) однородная система всегда совместна.

Возможны два случая:

1. r = n ( когда 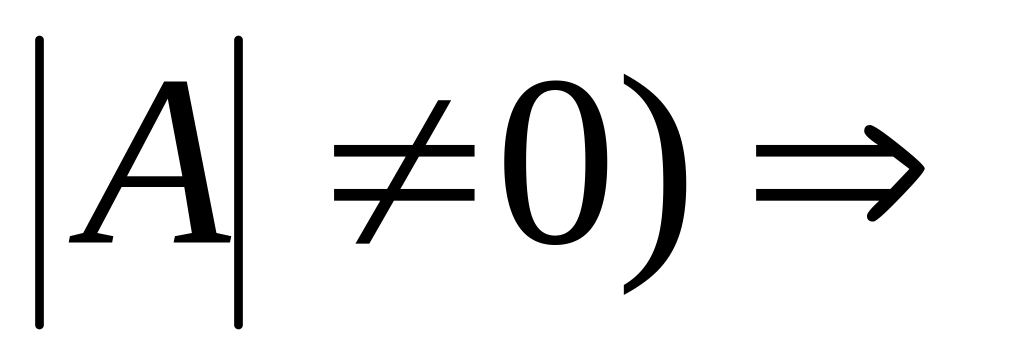единственное решение x₁=…=x_n=0

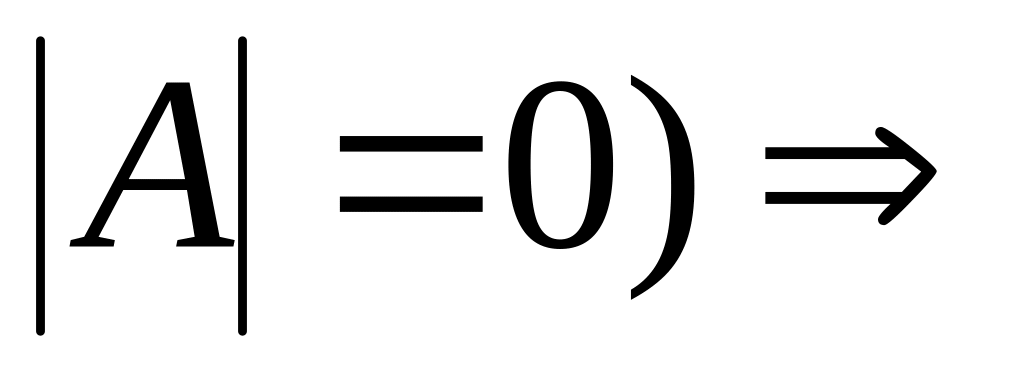2. r<n (когда бесконечное множество решений x₁,…,x_r – базисные неизвестные; x_r+1,…,x_n – свободные неизвестные.

Пример 9.1 Исследовать и решить систему

Ответ: , ,

Пример 9.2 Исследовать и решить систему

Ответ: бесконечное множество решений вида , , где

§10. Линейные отображения. Преобразования координат.

I.Основные понятия

Пусть в плоскости Р задана прямоугольная система координат.

Координаты точек вместо х, у будем обозначать х₁, х₂ или у₁, у₂.

Пусть (1) – уравнения, связывающие переменные х₁,х₂ с переменными у₁, у₂. а₁₁, а₁₂, а₂₁,а₂₂ – постоянные.

Каждой т. М Р с координатами х₁,х₂ соответствует единственная т. N Р с координатами у₁,у₂, которые определяются по (1).

Точка N называется образом точки М. Если точка М описывает на плоскости Р некоторую линию L, то ее образ также описывает некоторую линию.

С помощью (1) устанавливается отображение или преобразование плоскости Р в себя. Это отображение называется линейным.

Обозначим А = ; Х = ; У = .

Тогда Y = A ( ) – запись (1) в матричной форме.

А = – матрица линейного отображения

– определитель линейного отображения

– координаты образа вектора при линейном отображении, заданном матрицей А.

Если матрица А – невырожденная, т.е. , то отображение называется невырожденным или афинным.

Если , то отображение называется вырожденным.

Если отображение невырожденное (афинное), то из (1) по формулам Крамера получим:

;

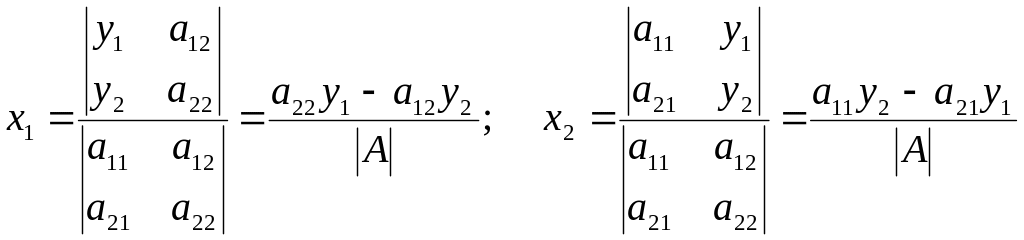(2)

По (1):

По (2): ед. т. М (х₁,х₂).

Итак, невырожденное (афинное) отображение определяет взаимно-однозначное отображение плоскости Р в себя.

Из (2) следует, что обратное отображение тоже невырожденное, а его матрица есть матрица, обратная А, т.е.

.

Формулы (2) можно получить другим способом:

Умножим (1) на А^-1:

Замечание. В трехмерном пространстве линейное отображение определяется системой уравнений.

– в матричном виде.

При аффинном (невырожденном) отображении образом плоскости является плоскость, а образом прямой – прямая.