1.2Уравнение теплопроводности

Рассмотрим задачу о распространении тепла в неравномерно нагретом твердом теле. Пусть и(x, y, z, t) – температура тела в точке (x, y, z) в момент времени t. Примем следующую модель процесса: происходит механический перенос тепла от точек с более высокой температурой к точкам с более низкой температурой: все тепло идет на изменение температуры тела; свойства тела не зависят от температуры, т.е. тело изотропно по отношению к температуре.

Возьмем внутри тела произвольный объем V, ограниченный замкнутой гладкой поверхностью S.

Количество тепла , проходящее через элементарную площадку dS с нормалью , за время dt определяется по закону Фурье , где k = k(x, y, z) – коэффициент теплопроводности, не зависящий от направления нормали . Тогда через поверхность S за промежуток времени t₂ – t₁, проходит количество тепла равное .

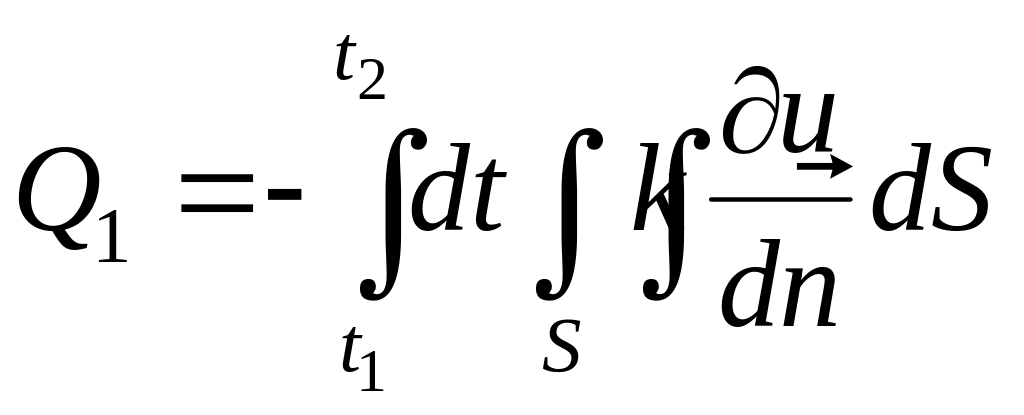Количество тепла , необходимое на изменение температуры элементарного объема dV на величину и(x, y, z, t₂) – и(x, y, z, t₁) определяется соотношением , где – удельная теплоемкость, – плотность вещества. Следовательно, на изменение температуры всего объема V требуется количество тепла равное

.

Предположим, что внутри тела имеются источники тепла. Обозначим через F(x, y, z, t) плотность тепловых источников (количество поглощенного или выделяемого тепла в единицу времени в единице объема), тогда количество тепла, выделяемого (поглощаемого) источниками тепла в объеме V за промежуток времени t₂ – t₁, будет равно .

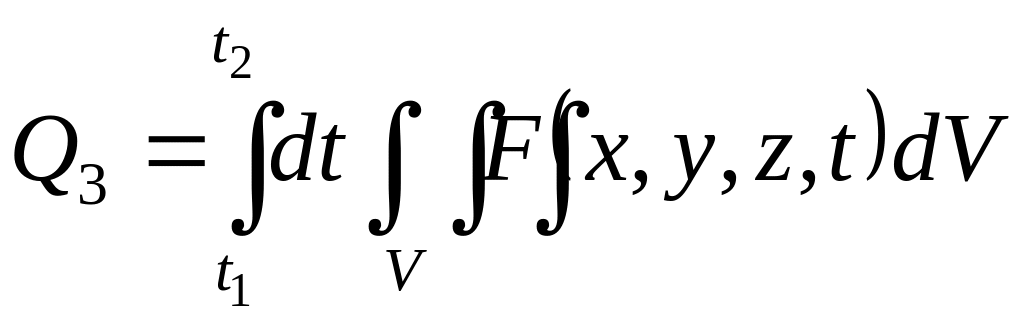Составим теперь уравнение баланса тепла для объема V. В рамках изучаемой модели количество поглощаемого тепла равно количеству выделяемого, т.е. .

Учитывая, что 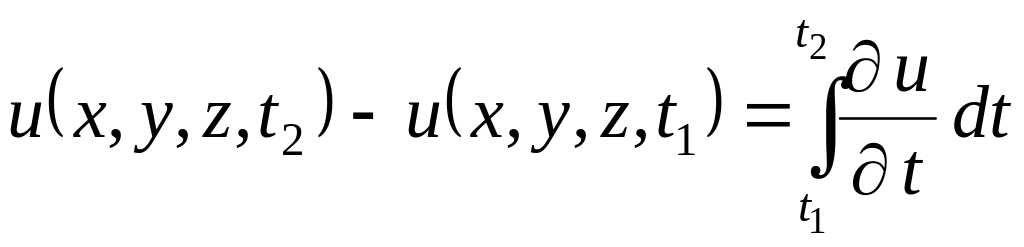и, по формуле Гаусса – Остроградского, , получим

.

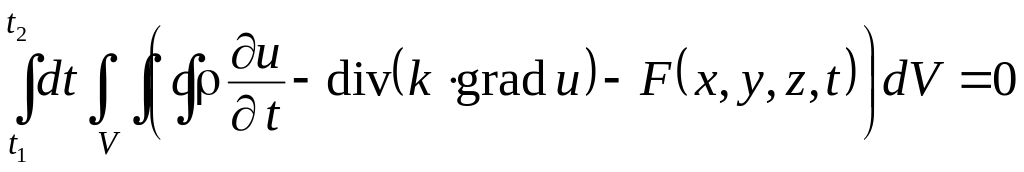В силу того что подынтегральная функция непрерывна, а объем V и промежуток времени t₂ – t₁ произвольны, для любой точки (x, y, z) и для любого момента времени t должно быть

. (1.5)

Это уравнение является уравнением теплопроводности неоднородного изотропного тела.

Если тело однородно, т.е. – const, то уравнение (2.1) можно переписать в виде

(1.6)

Совершенно аналогично выводится уравнение диффузии. При этом надо пользоваться законом Нернста для потока вещества w в направлении : . Здесь и(x, y, z, t) – концентрация диффундирующего вещества, D – коэффициент диффузии. Уравнение диффузии, таким образом, имеет вид

, (1.5’) где c – коэффициент пористости среды.

Задачи об отыскании установившейся температуры или концентрации приводят, очевидно, к следующему уравнению

. (1.7)

1.3Постановка краевых задач

При решении задач физики или других областей науки математическими методами необходимо прежде всего дать математическую постановку задачи. Однако интересующие нас явления носят, как правило, однозначный характер, в то время как описывающие их уравнения имеют множество решений. Поэтому при математической постановке задачи недостаточно написать уравнение (или систему), которому удовлетворяет искомая функция (система функций). Надо также указать дополнительные условия, позволяющие выделить лишь одно интересующее нас решение, описывающее конкретное явление, процесс. При этом дополнительных условий должно быть не слишком много, чтобы существовало решение, удовлетворяющее им. Таким образом, дополнительные условия должны обеспечить существование и единственность решения.

Характер дополнительных условий покажем далее на примерах задач.

Например, в случае колебаний струны или стержня (уравнения (1.1) и (1.3)) надо задать начальный профиль и начальную скорость точек струны (стержня). Это начальные условия. Аналогичный вид они имеют для любого волнового уравнения.

Кроме того, надо записать режим на концах (краях) струны (стержня).

Так, если задан закон движения концов то мы будем называть такие дополнительные условия краевыми (граничными) условиями первого типа.

Если задан закон изменения силы, приложенной к концу струны (стержня) и действующей в направлении колебаний, то режим на концах можно записать следующим образом:

или .

Это краевые условия второго типа.

Пусть к концу стержня (x=l) прикреплена пружина, действующая вдоль оси x. Тогда сила натяжения на конце будет уравновешиваться силой действия пружины, равной . Краевой режим на этом конце запишется в виде: где – коэффициент жесткости пружины, или

Если пружина в свою очередь движется по закону то краевой режим можно представить следующим образом: Это краевое условие третьего типа. На левом конце x= 0 оно имеет вид:

Для двух- и трехмерного случаев рассмотренные типы краевых условий имеют следующий вид:

(первый тип), (1.8)

(второй тип), (1.9)

(третий тип). (1.10)

Здесь – производная по внешней нормали к поверхности S.

Такие же краевые условия встречаются в задачах, приводящихся к уравнениям параболического типа. Так, если задается температура на поверхности тела, то имеем краевое условие первого типа. Если задается плотность потока тепла – через поверхность тела S, то имеем краевое условие второго типа. Если же на поверхности тела происходит теплообмен со средой, имеющей температуру , по закону Ньютона – , то имеем краевое условие третьего типа.

Встречаются и другие типы краевых условий. Рассмотренные типы краевых условий являются линейными, поскольку искомая функция и ее производные входят в них линейно. Они называются однородными, если их правые части тождественно равны нулю, и неоднородными – в противном случае.

Если нас будут интересовать значения искомой функции в точках, настолько удаленных от границы, что влиянием условий на границах можно пренебречь, то оправдана постановка задачи без краевых условий, т.е. задачи Коши.

В тех случаях, когда можно выделить круговую относительно некоторой оси или сферическую относительно некоторого центра симметрию по пространственным переменным, целесообразно уравнения и дополнительные условия записывать в цилиндрических или сферических координатах соответственно. В цилиндрических координатах оператор Лапласа принимает следующий вид .

В сферических координатах –

.