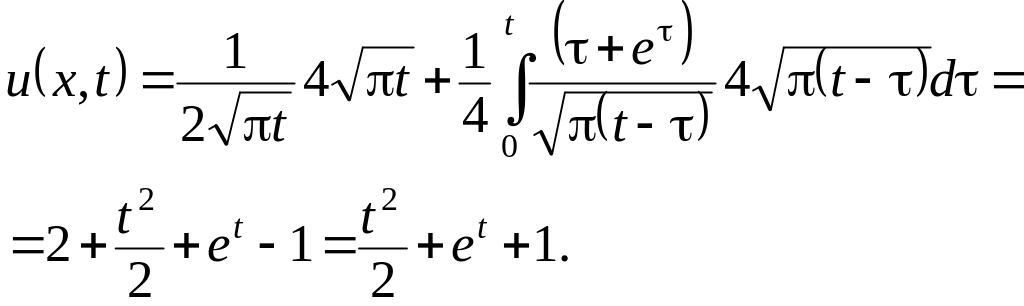- •1Вывод уравнений математической физики и постановка краевых задач
- •1.1Уравнение малых поперечных колебаний струны
- •1.2Уравнение теплопроводности
- •1.3Постановка краевых задач
- •1.4Задачи
- •2Классификация линейных уравнений второго порядка и приведение их к каноническому виду
- •2.1Классификация уравнений
- •2.2Приведение уравнений с двумя независимыми переменными к каноническому виду
- •2.3Приведение к простейшему виду
- •2.4Задачи
- •3Методы, наиболее часто применяемые при решении задач для уравнений с частными производными
- •3.1Задача Коши для волнового уравнения. Метод характеристик
- •3.1.1Решение задачи Коши на прямой
- •3.2.2Решение задач с неоднородным краевым условием
- •3.2.3Задачи
- •3.3Решение задачи Коши для уравнения теплопроводности
- •3.3.1Формула Пуассона
- •3.3.2Задачи
- •3.4Метод разделения переменных решения смешанных задач
- •3.4.1Сущность метода
- •3.4.2Метод Фурье решения смешанных задач для уравнений гиперболического типа
- •3.4.3Метод Фурье решения смешанных задач для уравнений параболического типа
- •3.4.4Решение неоднородных задач методом Фурье
- •3.4.5Метод Фурье решения краевых задач для уравнений эллиптического типа
- •3.4.6Задачи
- •Рекомендуемая литература
- •Содержание
3.2.2Решение задач с неоднородным краевым условием
Перейдем к рассмотрению задачи для уравнения (3.1) с неоднородными краевыми условиями
![]()
Эта задача в силу ее линейности может быть разбита на две
![]() и
и
![]()
При этом
![]() .
Первая задача решается приведенным
выше способом, решение второй задачи
ищется в виде прямой волны
.
Первая задача решается приведенным
выше способом, решение второй задачи
ищется в виде прямой волны
![]() ,
так как краевой режим является
единственной причиной возбуждения
колебаний в струне. Тогда из начальных
условий
,
так как краевой режим является
единственной причиной возбуждения
колебаний в струне. Тогда из начальных
условий
![]() .
Из краевого условия
.
Из краевого условия
![]() .
Таким образом
.
Таким образом
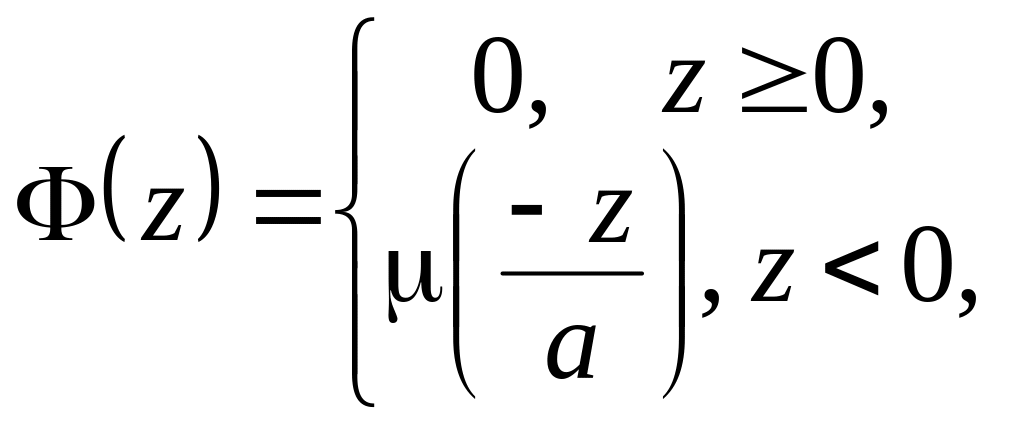 т.е.
т.е.
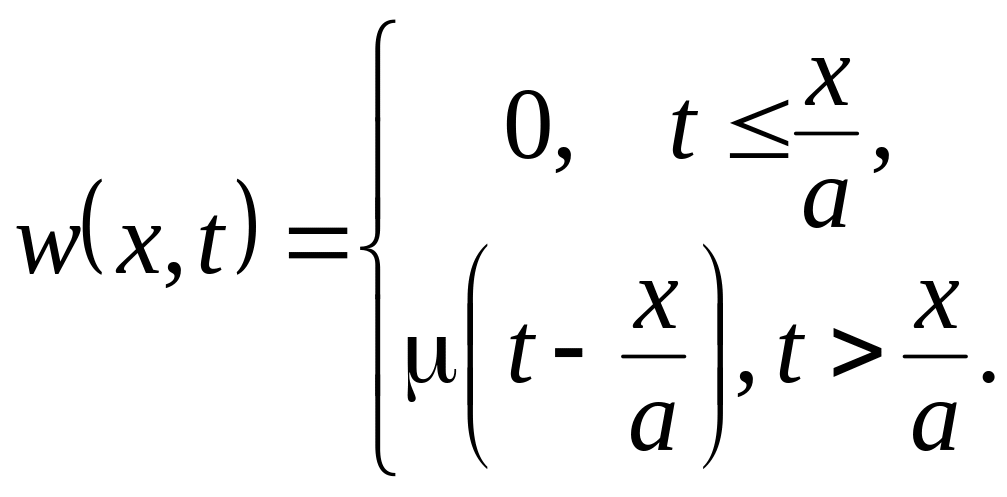 (3.10)
(3.10)
Пример 6. Решить смешанную задачу
![]()
Решение. Разобьем исходную задачу на две
![]() и
и
![]()
при этом
![]() .
Решение первой задачи, пользуясь
формулой (3.8), можно записать
.
Решение первой задачи, пользуясь
формулой (3.8), можно записать
 или
или
![]()
Решение второй задачи в
соответствии с формулой (3.10)
![]() .
Тогда
.
Тогда
![]() .
.
Пример 7. Решить смешанную задачу
![]()
Решение.
При помощи замены переменных
![]() приводим уравнение к каноническому
виду (см. раздел 2.2)
приводим уравнение к каноническому
виду (см. раздел 2.2)
![]() ,
из которого находим
,
из которого находим
![]() .
Здесь
.
Здесь
![]() и
и
![]() произвольные дважды непрерывно
дифференцируемые функции. Выполнив
обратную замену переменных,
получим общее решение исходного
уравнения
произвольные дважды непрерывно
дифференцируемые функции. Выполнив
обратную замену переменных,
получим общее решение исходного
уравнения
![]() .
Неизвестные функции найдем из начальных
и краевого условий:
.
Неизвестные функции найдем из начальных
и краевого условий:
![]()
Из первых двух уравнений
системы находим
![]() ,
,
![]() при
при
![]() .
Подставляя найденную функцию
.
Подставляя найденную функцию
![]() в третье уравнение системы, получим
в третье уравнение системы, получим
![]() .
Следовательно, решением задачи является
функция
.
Следовательно, решением задачи является
функция
![]() или
или
![]()
3.2.3Задачи
Решить смешанные задачи:

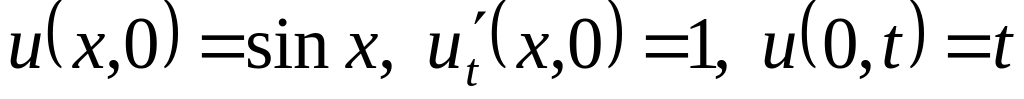 .
.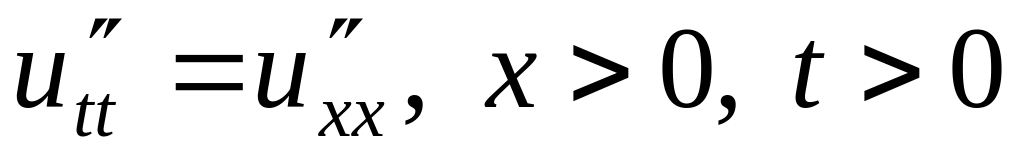 ,
,
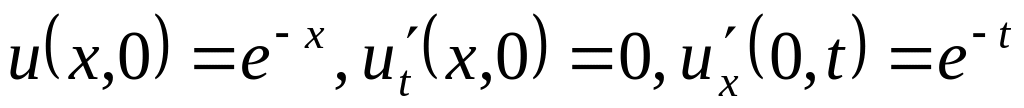 .
.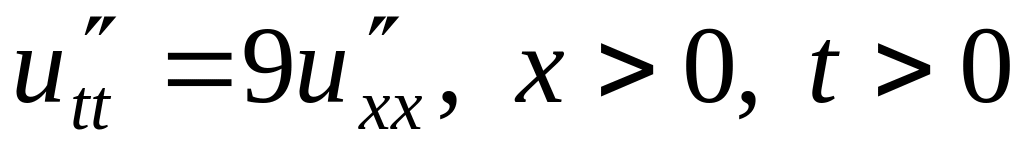 ,
,
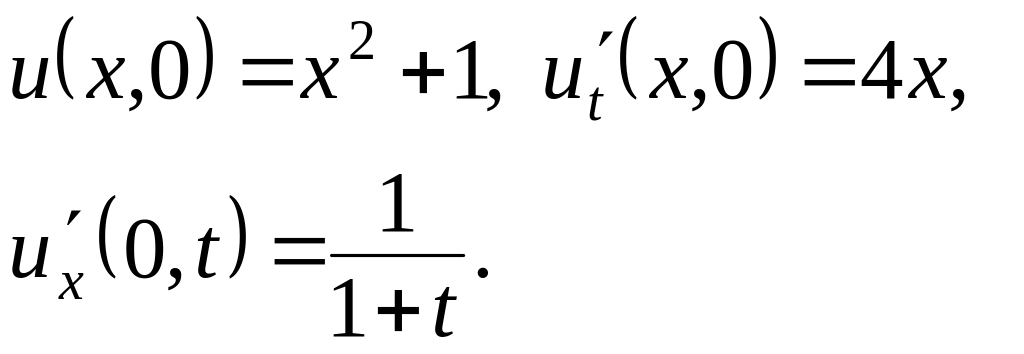
,
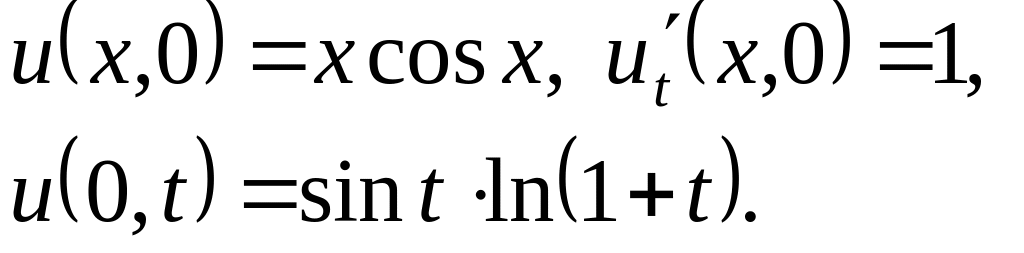
,
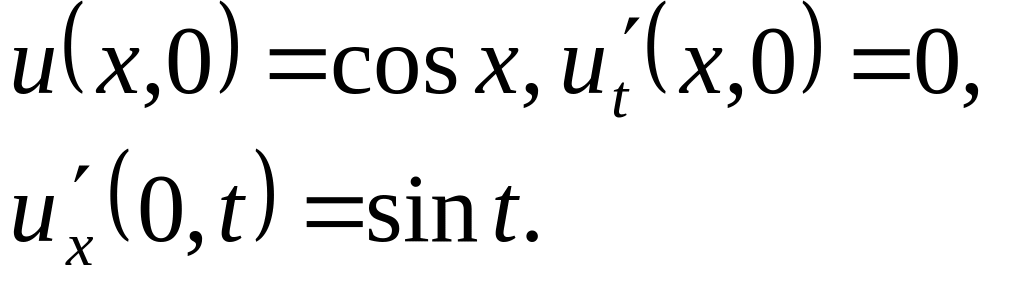
,
 .
.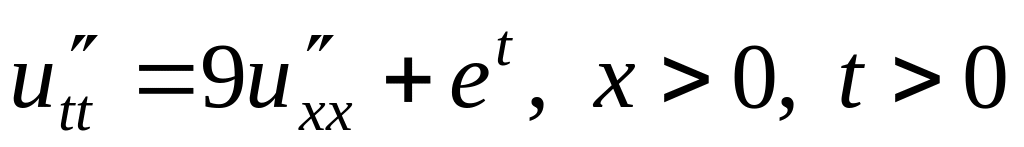 ,
,
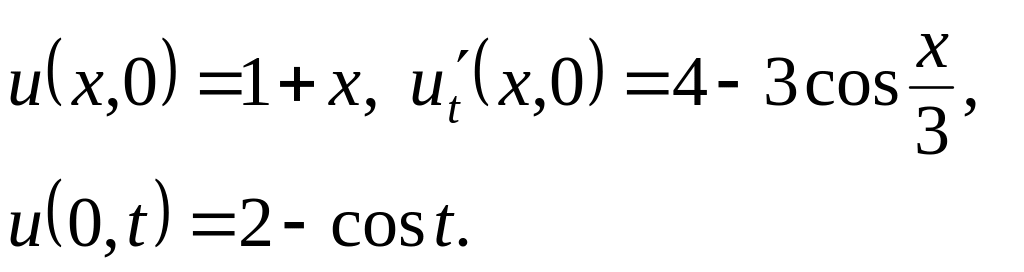
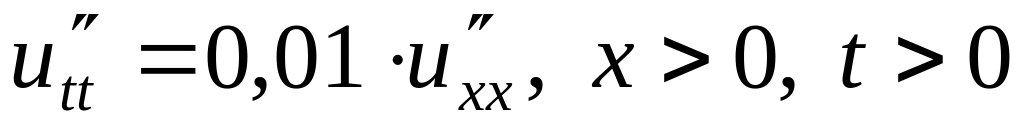 ,
,
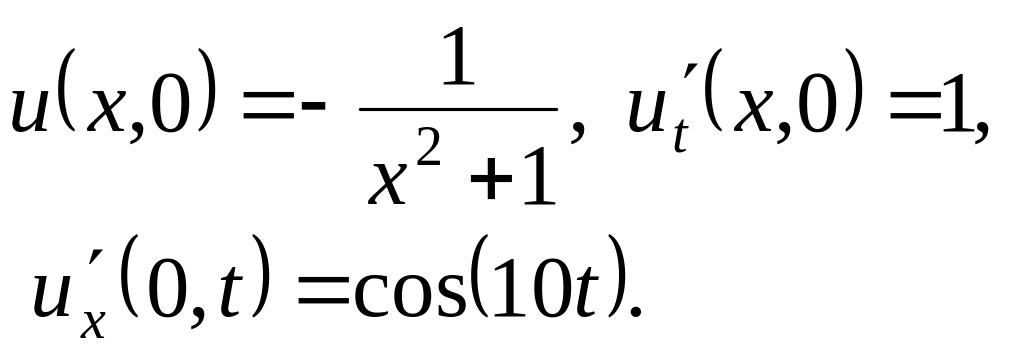
 ,
,
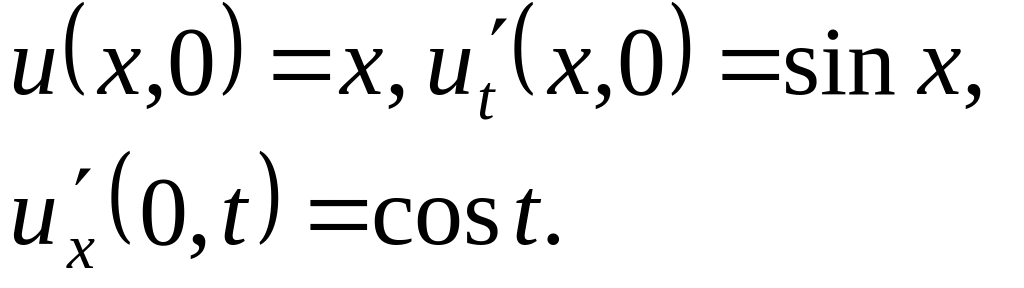
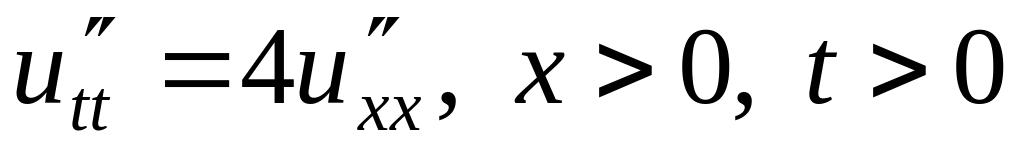 ,
,
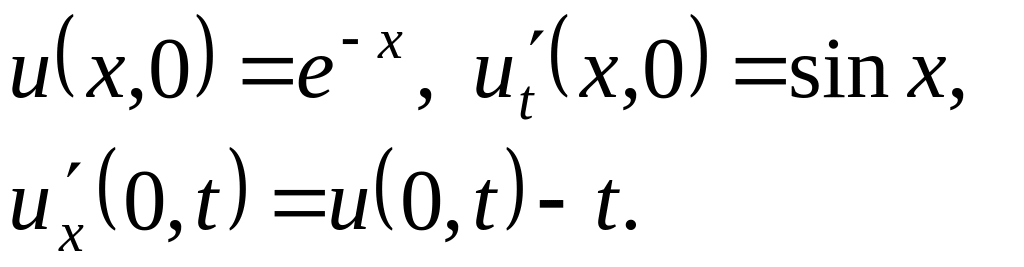
3.3Решение задачи Коши для уравнения теплопроводности
3.3.1Формула Пуассона
Классической
задачей Коши для уравнения теплопроводности
называется задача о нахождении функции
![]() ,
характеризующей температуру в точке
пространства
,
характеризующей температуру в точке
пространства
![]() в момент времени
в момент времени
![]() .
Функция
удовлетворяет уравнению
.
Функция
удовлетворяет уравнению
![]() , (3.11)
, (3.11)
описывающему процесс распространения тепла в однородном изотропном пространстве, и начальному условию
![]() , (3.12)
, (3.12)
задающему начальное распределение температур. Функция f характеризует интенсивность внутренних источников тепла.
Если функция
![]() ,
а функция
,
а функция
![]() и ограничена, то решение задачи Коши
(3.11), (3.12) существует, единственно и
выражается формулой Пуассона
и ограничена, то решение задачи Коши
(3.11), (3.12) существует, единственно и
выражается формулой Пуассона
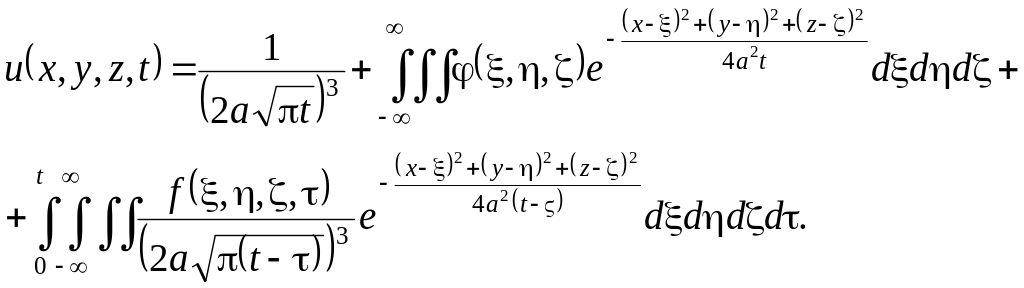 (3.13)
(3.13)
Очевидно, для случая одной пространственной переменной задача Коши запишется
![]() , (3.11’)
, (3.11’)
![]() . (3.12’)
. (3.12’)
И формула Пуассона соответственно примет вид:
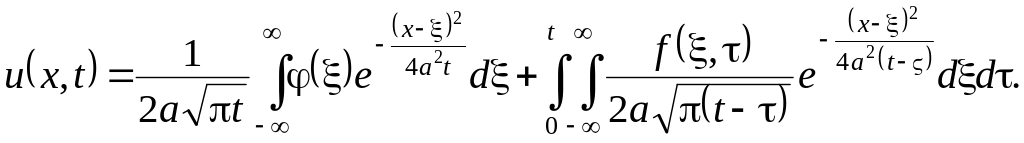 (3.13’)
(3.13’)
При решении
задач для уравнения теплопроводности
(3.11) на полупрямой применяются те же
подходы, что и при решении задач для
волнового уравнения на полупрямой (см.
п. 3.2). Положим в уравнении (3.11’)
![]() .
При этом выбор характера продолжения
заданных условий на всю ось определяется
следующими леммами.
.
При этом выбор характера продолжения
заданных условий на всю ось определяется
следующими леммами.
Лемма 3.
Пусть в задаче (3.11’), (3.12’) функция
![]() нечетная относительно x=0, т.е.
нечетная относительно x=0, т.е.
![]() ,
тогда
.
,
тогда
.
Лемма 4.
Пусть в задаче (3.11’), (3.12’) функция
![]() четная относительно x=0, т.е.
четная относительно x=0, т.е.
![]() ,
тогда
,
тогда
![]() .
.
Пример 8. Решить задачу:
![]()
![]()
Решение. Для решения задачи воспользуемся формулой Пуассона (3.13’). При этом получим
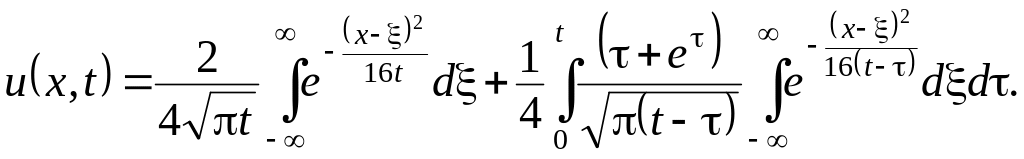
Посчитаем
первый интеграл, для этого введем новую
переменную![]() и воспользуемся табличным значением
интеграла
и воспользуемся табличным значением
интеграла

Тогда решение можно переписать следующим образом: