3.3.2Задачи
.
.
.
.
.
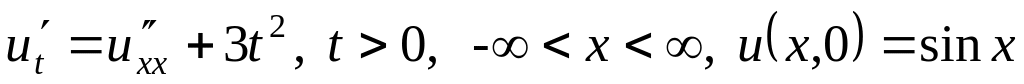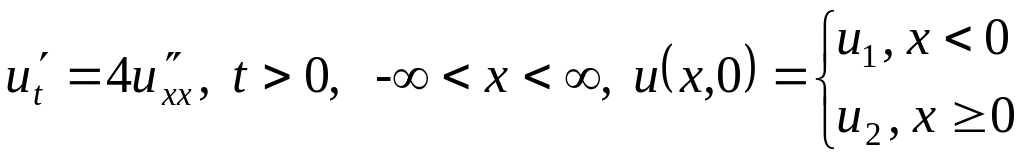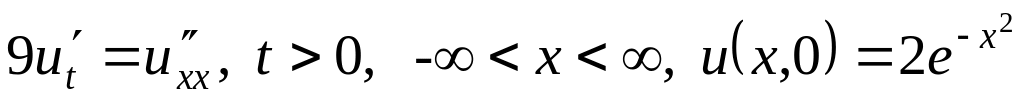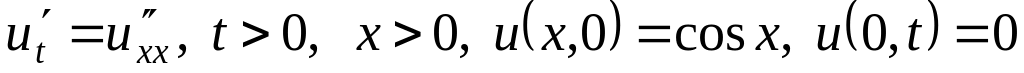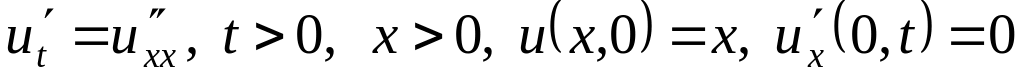3.4Метод разделения переменных решения смешанных задач
3.4.1Сущность метода
Пусть
в области D, ограниченной
замкнутой кусочно-гладкой поверхностью
S, для
требуется найти функцию
,
удовлетворяющую уравнению
, (3.14)
граничным условиям
(3.15)
и начальным
, (3.16)
соответственно
. (3.16’)
– линейный дифференциальный оператор
второго порядка по пространственным
переменным.
Идея метода Фурье (разделения переменных) заключается в следующем.
А) Ищем
нетривиальное (не равное тождественно
нулю) решение уравнения (3.14), удовлетворяющее
только краевым условиям (3.15), среди
функций вида
.
Подставив функцию
в уравнение (3.14) и разделив обе части
уравнения на
,
получим
(соответственно
).
Для тождественного выполнения этого
равенства, необходимо и достаточно,
чтобы обе дроби были равны одной и той
же константе:
.
Таким образом, должны выполняться
тождества
, (3.17)
, (3.18)
причем функция Ф(М) должна удовлетворять краевому условию
.
(3.19)
Задачу (3.18), (3.19) называют задачей Штурма – Лиувиля. Она имеет нетривиальное решение не при всех значениях .
Определение.
Те значения , при
которых задача (3.18), (3.19) имеет нетривиальные
решения, называют собственными
значениями, а соответствующие им
нетривиальные решения
– собственными функциями.
Б) Решаем задачу
Штурма – Лиувиля. Она имеет счетное
количество решений. Пусть
суть собственные функции этой задачи,
а
–
отвечающие им собственные значения.
В) Для каждого
собственного значения n
находим решение уравнения (3.17). Общее
его решение имеет вид
для уравнения (3.14) гиперболического
типа и
для уравнения (3.14) параболического
типа.
Таким образом, частными решениями уравнения (3.14), удовлетворяющими только краевым условиям (3.15) являются функции
,
или
соответственно.
Г) Взяв сумму таких частных решений по всем собственным функциям, получим общее решение уравнения (3.14), удовлетворяющее краевым условиям (3.15)
(3.20)
или
. (3.20’)
Коэффициенты Cn и Dn находим из начальных условий (3.16), (3.16’) в виде
,
,
.
3.4.2Метод Фурье решения смешанных задач для уравнений гиперболического типа
Рассмотрим задачу о свободных колебаниях однородной струны длины l, закрепленной на концах. Эта задача сводится к решению уравнения (3.1) при начальных условиях (3.2) и граничных условиях
. (3.21)
Будем сначала
искать нетривиальные частные решения
уравнения (3.1), удовлетворяющие условиям
(3.21), в виде
.
Тогда из уравнения (3.1) получим
(3.22)
. (3.23)
Из граничных
условий (3.21) и требования нетривиальности
решения вытекают условия
.
Таким образом, приходим к задаче Штурма – Лиувилля
.
Найдем собственные числа и собственные функции этой задачи. Рассмотрим отдельно случаи, когда коэффициент положителен, отрицателен и равен нулю.
При <0
общее решение примет вид
,
тогда из граничных условий
.
При =0
общее решение примет вид
,
тогда из граничных условий
.
При >0
общее решение примет вид
,
тогда из граничных условий
Найденным собственным числам соответствуют
собственные функции
.
При
из (3.23) находим
.
Поэтому функция
удовлетворяет уравнению (3.1) и граничным
условиям (3.21) при любых an,
bn.
Тогда общее решение уравнения (3.1), удовлетворяющее условиям (3.21), запишем в виде ряда:
. (3.24)
Постоянные an, bn определим из начальных условий. Подставляя (3.24) в (3.2), приходим к равенствам
.
Данные формулы
дают разложения функций
в ряд Фурье на интервале
.
Известно, что коэффициенты этих
разложений вычисляются по формулам
(3.25)
Пример 9.
Пусть струна, закрепленная на концах
x=0, x=1,
имеет в начальный момент форму параболы
.
Определим смещение точек струны от оси
абсцисс, если начальные скорости
отсутствуют (рис. 3.1)
Решение.
Для уравнения (3.1) заданы начальные
условия
и граничные условия (3.21). Пусть a=1.
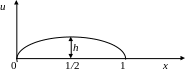
Рис. 3.1
Тогда решение задачи будет иметь вид
,
в котором коэффициенты an, bn находим из соотношений
Дважды интегрируем по частям
.
Подставляя значения коэффициентов, получим
Если n=2k,
то
,
а если n=2k+1,
то
,
поэтому окончательно будем иметь
