
- •1 Действительные числа
- •1.1 Логическая символика и терминология
- •1.2 Аксиоматика действительных чисел
- •1.3 Точные грани числовых множеств
- •1.4 Натуральные, рациональные, иррациональные числа
- •1.5 Принцип Кантора
- •1.6 Правило построения отрицания
- •2 Числовые последовательности
- •2.1 Определения
- •2.2 Предел последовательности
- •2.3 Общие свойства предела последовательности
- •2.4 Свойства сходящихся последовательностей, связанные с неравенствами
- •2.5 Бесконечно малые последовательности
- •2.6 Бесконечно большие последовательности
- •2.7 Арифметические операции над сходящимися последовательностями
- •2.8 Предел монотонной последовательности
- •2.9 Число e
- •2.10 Подпоследовательности. Частичные пределы
- •2.11 Критерий Коши сходимости последовательности
- •3 Предел функции в точке
- •3.1 Определение предела по Коши
- •3.2 Определение предела по Гейне
- •3.3 Различные типы пределов
- •3.4 Свойства пределов функции в точке
- •3.5 Предел монотонной функции
- •3.6 Бесконечно малые функции
- •3.7 Замена переменной при вычислении предела (или предел композиции функций)
- •3.8 Первый замечательный предел
- •3.9 Второй замечательный предел
- •3.10 Сравнение асимптотического поведения функций
- •4 Непрерывные функции
- •4.1 Определение
- •4.2 Точки разрыва
- •4.3 Свойства функций, непрерывных в точке (локальные свойства непрерывных функций)
- •4.4 Свойства функций, непрерывных на отрезке (глобальные свойства непрерывных функций)
- •5 Производная функции в точке
- •5 .1 Определение. Физический и геометрический смысл производной
- •5.2 Дифференциал функции
- •5.3 Правила дифференцирования
- •5.4 Дифференцирование параметрически заданных
- •5.5 Производные и дифференциалы высших порядков
- •6 Основные теоремы для дифференцируемых функций
- •6.1 Точки локального экстремума
- •6.2 Теорема Ферма
- •6.3 Теорема Ролля
- •7 Формула Тейлора
- •Формулы Маклорена для некоторых элементарных функций
- •8 Правило Лопиталя
- •9 Исследование функций с помощью производной
- •9.1 Возрастание и убывание функций
- •9.2 Экстремумы функции
- •9.3 Наибольшее и наименьшее значения функции на отрезке
- •9.4 Выпуклость функции
- •9.5 Точки перегиба
- •9.6 Асимптоты
- •9.7 Схема исследования функции
1.4 Натуральные, рациональные, иррациональные числа
О. Множество М называется индуктивным, если
![]() .
.
О.
Множество натуральных чисел – это
наименьшее индуктивное множество,
содержащее 1. Обозначается N
![]() .
.
О. Множество целых чисел – это множество
Z
![]() N
N
![]() .
.
О. Множество рациональных чисел – это множество
Q
![]() целое,
целое,
![]() натуральное
натуральное![]() .
.
Числа, которые не являются рациональными, называются иррациональными.
Любое рациональное
число можно представить в виде конечной
или бесконечной периодической десятичной
дроби. Например,
![]() .
Иррациональное число – это всегда
бесконечная непериодическая десятичная
дробь.
.
Иррациональное число – это всегда
бесконечная непериодическая десятичная
дробь.
Принцип Архимеда Множество N не ограничено сверху.
Доказательство.
Допустим, N
– ограничено
сверху. Тогда оно имеет точную верхнюю
грань. Обозначим
![]() .
Тогда для числа
.
Тогда для числа
![]()
![]() .
Но тогда
.
Но тогда
![]() ,
т.е. М
не является
,
т.е. М
не является
![]() .
Противоречие. ■
.
Противоречие. ■
Следствие 1 из
принципа Архимеда
![]() .
.
Доказательство.
Возьмем
![]() .
Рассмотрим число
.
Рассмотрим число
![]() .
Оно не является верхней гранью для N
(так как N
не ограничено
сверху). Значит,
.
Оно не является верхней гранью для N
(так как N
не ограничено
сверху). Значит,
![]() .
Следовательно,
.
Следовательно,
![]() .■
.■
Следствие 2
Если
![]() и
и
![]() ,
то
,
то
![]() .
.
Доказательство.
Допустим,
![]() .
Тогда
.
Тогда
![]() .
.
Противоречие с условием. ■
Следствие 3
Для
![]() :
:
![]()
![]() .
.
1.5 Принцип Кантора
Примеры числовых
множеств: отрезок, интервал, полуинтервал,
луч, прямая, пустое множество, N,
Q
и т.п. Из множеств можно образовывать
системы множеств. Например,
![]() ,
,
![]() .
.
Утверждение
Для системы
интервалов
не существует точки, общей для всех
интервалов, т.е.
![]() Ø.
Ø.
Доказательство.
Допустим, существует общая точка. Это
число не может быть отрицательным. Это
и не ноль. Допустим, существует число
![]() .
По следствию 1 из принципа Архимеда,
.
По следствию 1 из принципа Архимеда,
![]() .
Но тогда
.
Но тогда
![]() .
Противоречие. ■
.
Противоречие. ■
Пусть имеется
система множеств
![]() .
Если
.
Если
![]() ,
т.е.
,
т.е.
![]() ,
то эта система называется системой
вложенных множеств.
,
то эта система называется системой
вложенных множеств.
Принцип Кантора
Для любой системы вложенных отрезков
![]() существует точка, общая для всех отрезков,
т.е.
существует точка, общая для всех отрезков,
т.е.
![]() .
Если, кроме того, система отрезков
такова, что
.
Если, кроме того, система отрезков
такова, что
![]() существует отрезок, длина которого
меньше
существует отрезок, длина которого
меньше
![]() ,
то точка с
– единственная.
,
то точка с
– единственная.
Доказательство.
Пусть
![]() .
.
Рассмотрим два
множества:
![]() и
и
![]() (А
– левые концы
(А
– левые концы
![]() ,
В
– правые концы
).
Нетрудно
доказать (от противного), что
,
В
– правые концы
).
Нетрудно
доказать (от противного), что
![]()
![]() (иначе бы
(иначе бы
![]() ,
и они бы не пересекались). Значит, по
аксиоме полноты,
,
и они бы не пересекались). Значит, по
аксиоме полноты,
![]() ,
в том числе и для случая
,
в том числе и для случая
![]() тоже.
тоже.
Значит,
![]() ,
,
![]()
![]() .
.
Допустим теперь,
![]() ,
общие для всех отрезков. Пусть
,
общие для всех отрезков. Пусть
![]() .
Возьмем в качестве
.
Возьмем в качестве
![]() .
Тогда существует отрезок
.
Тогда существует отрезок
![]() длины меньше
.
Так как
длины меньше
.
Так как
![]() и
и
![]() ,
то длина
равна
,
то длина
равна
![]() .
Но, по построению, длина
меньше
.
Но, по построению, длина
меньше
![]() .
Противоречие. ■
.
Противоречие. ■
1.6 Правило построения отрицания
Пусть
![]() некоторое
свойство, обозначим
некоторое
свойство, обозначим
![]() противоположное
к нему свойство.
противоположное
к нему свойство.
-
Утверждение
Отрицание (противоположное утверждение)
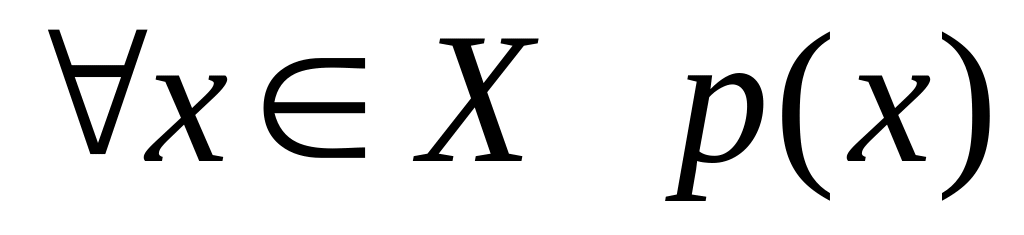
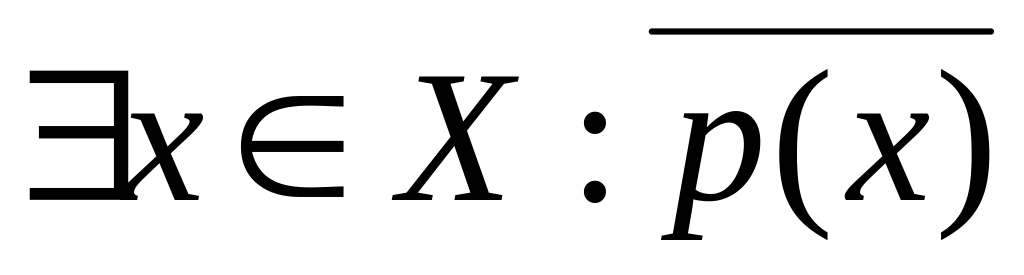
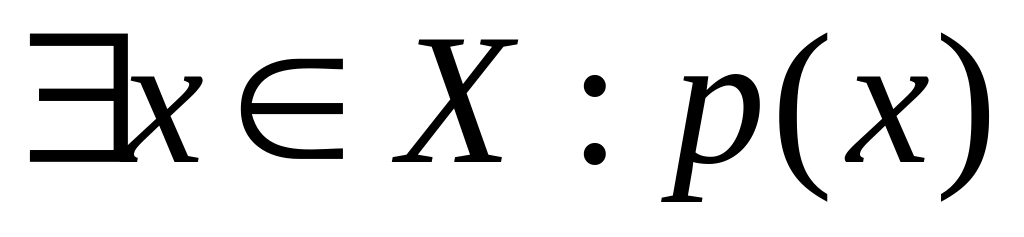
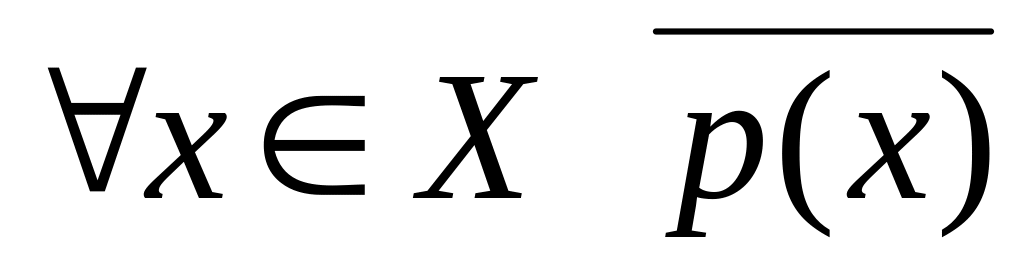
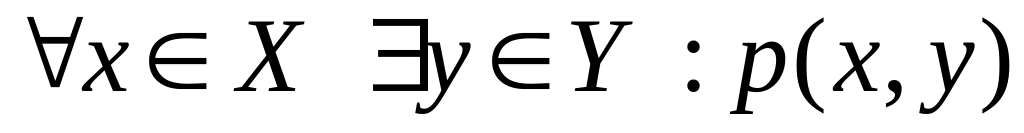
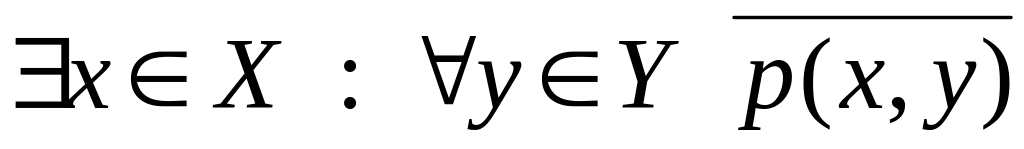
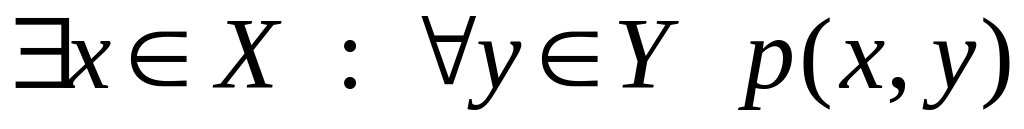
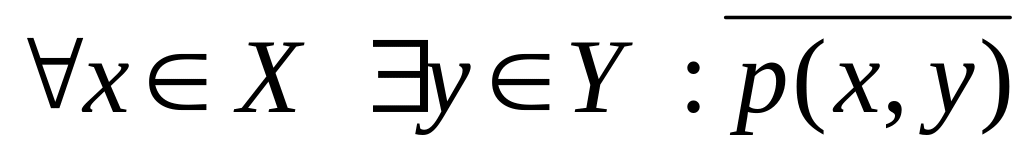
2 Числовые последовательности
2.1 Определения
Функцией называется правило (закон), по которому каждому элементу множества Х ставится в соответствие единственный элемент множества Y.
Обозначается
![]() или
или
![]() .
Множество Х
при этом называется областью
определения,
а множество Y
– областью
значений.
.
Множество Х
при этом называется областью
определения,
а множество Y
– областью
значений.
Последовательность – это функция, область определения которой есть множество N всех натуральных чисел.
![]() – n-ый
член последовательности,
номер
члена
.
– n-ый
член последовательности,
номер
члена
.
Примеры
![]() .
.
О. Последовательность называется ограниченной сверху, если
![]() :
:
![]() .
.
О. Последовательность называется ограниченной снизу, если
![]() :
:
![]() .
.
О. Последовательность называется ограниченной, если
:
![]() .
.
О. Последовательность
называется возрастающей
с номера
![]() ,
если
,
если
![]()
![]() .
.
О. Последовательность называется убывающей с номера , если
![]() .
.
