3.5 Предел монотонной функции
О. Функция называется возрастающей на множестве Х, если
.
О. Функция называется неубывающей на множестве Х, если
.
О. Функция называется убывающей на множестве Х, если
.
О. Функция называется невозрастающей на множестве Х, если
.
Теорема 1
Для того,
чтобы неубывающая функция
имела предел при
или
,
необходимо и достаточно, чтобы функция
была ограничена на Х
сверху.
Теорема 2
Для того,
чтобы невозрастающая функция
имела предел при
или
,
необходимо и достаточно, чтобы функция
была ограничена на Х
снизу.
3.6 Бесконечно малые функции
О.
Если
,
то функцию
называют бесконечно малой при
Свойства бесконечно малых функций
1) Сумма конечного
числа б.м. функций при
есть б.м. функция при
2) Произведение б.м. функции на ограниченную в некоторой проколотой окрестности точки a функцию есть б.м. функция при
3) Произведение конечного числа б.м. функций при есть б.м. функция при
3.7 Замена переменной при вычислении предела (или предел композиции функций)
Теорема
Если
и
,
причем для любого х
из некоторой
проколотой окрестности точки
a
,
то в точке a
существует
предел сложной функции
и справедливо равенство:
.
3.8 Первый замечательный предел
Теорема
.
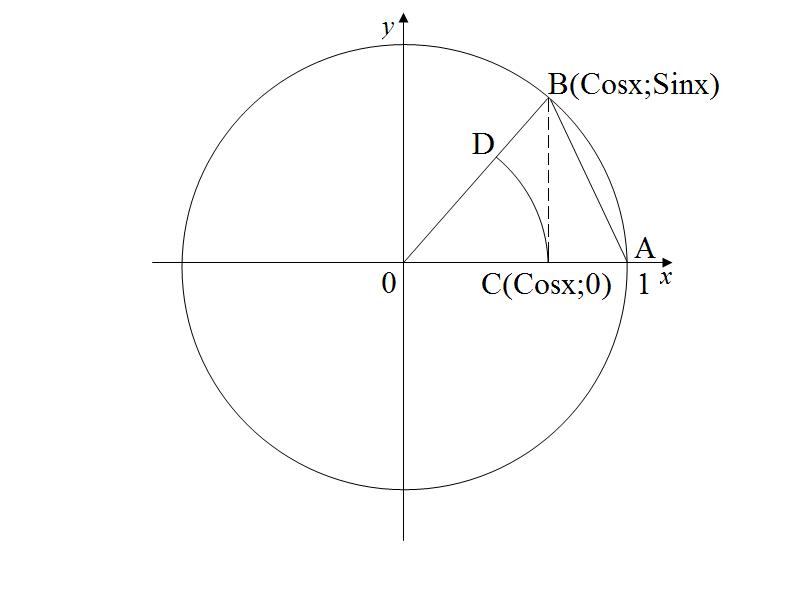
Доказательство.
Покажем сначала, что
при
.
Так как все функции, входящие в неравенство,
чётные, то рассмотрим случай
.
Очевидно, площадь
криволинейного сектора OCD
меньше площади треугольника OAB,
а она меньше площади криволинейного
сектора OAB.
Воспользуемся формулой площади
криволинейного сектора:
(r
− радиус, х
– центральный угол). Тогда
.
Разделим все части
последнего неравенства на х
и умножим на два, получим
.
Переходя к пределу при
во всех час-тях последнего неравенства,
получим, что и требовалось доказать.■
3.9 Второй замечательный предел
Сделав в последнем
пределе замену
,
получим
.
Утверждение
Если
и
,
то
.
Пример 1
.
Пример 2
.
В последнем примере
при
получим
.
3.10 Сравнение асимптотического поведения функций
а) Эквивалентные функции.
О.
Если в некоторой проколотой окрестности
точки
функция
представима в виде
,
причем
,
то функции
и
называют эквивалентными
при
и пишут
при
.
Утверждение
Если
и
в некоторой
,
то
при
тогда, и только тогда, когда
.
Например, при
,
так как
;
,
так как
.
Таблица эквивалентных функций при
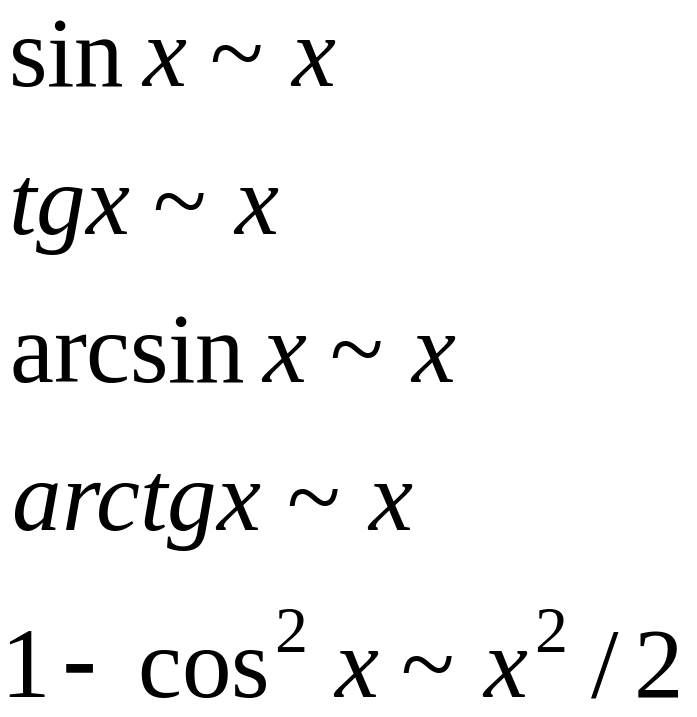
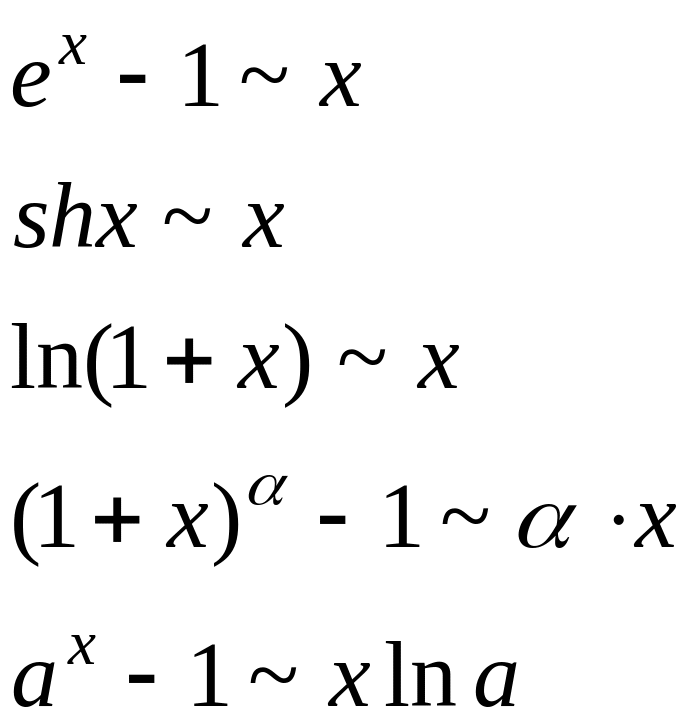
Теорема
Если
и
при
,
то
.
б) Понятие бесконечно малой функции по сравнению с другой.
О.
Если в некоторой проколотой окрестности
точки
функция
представима в виде
,
причем
,
то функцию
называют бесконечно
малой по сравнению с
при
и пишут
,
.
Утверждение
Если
в некоторой
,
то
при
тогда, и только тогда, когда
.
Пример
1) при
;
2) при
.
Если и − обе бесконечно малые при , то говорят, что есть бесконечно малая более высокого порядка, чем при .
Некоторые важные
свойства символа
.
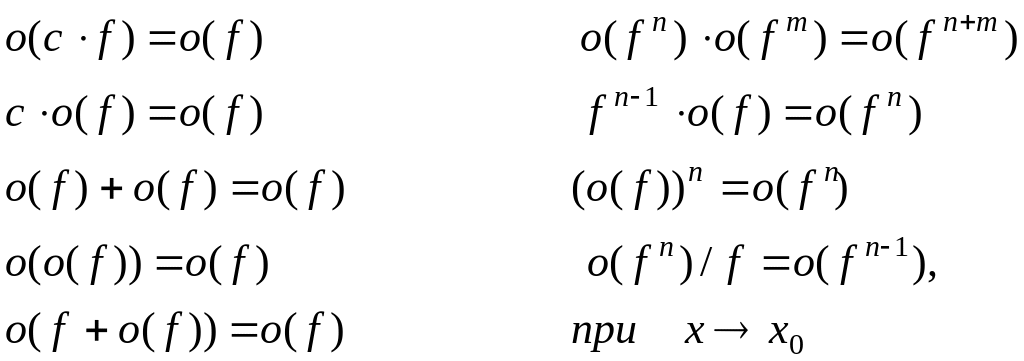
Докажем, например,
что
.
Действительно,
,
так как если
и
бесконечно
малые, то
тоже
бесконечно малая ■