Введение

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. В этой дисциплине рассматриваются теоретические модели, приложимые к любым массовым явлениям в природе, обществе и технике. Знание этих общих законов позволяет делать заключения о закономерностях, имеющих место в каждом конкретном случае.

В свою очередь, на основе теории вероятностей разрабатываются методы математической статистики, которые широко применяются при обработке результатов исследований. Приведем основную программу этой части курса высшей математики:

1. Случайные события. Основные понятия теории вероятностей.

2. Вероятность суммы событий.

3. Вероятность произведения событий.

4. Формула полной вероятности и формула Байеса.

5. Повторение независимых опытов и теоремы Лапласа.

6. Теорема Бернулли и закон Пуассона.

7. Случайные величины. Закон распределения и функция распределения.

8. Математическое ожидание случайной величины.

9. Дисперсия и среднее отклонение случайной величины.

10. Биномиальный закон распределения и закон Пуассона.

11. Равномерный и нормальный законы распределения.

12. Система двух случайных величин. Закон и функция распределения.

13. Условный закон распределения и условное математическое ожидание.

14. Начальные и центральные моменты случайной величины и системы случайных величин. Коэффициент корреляции.

15. Выборка и эмпирическое распределение. Графическое представление.

16. Точечные оценки параметров распределения по эмпирическим данным.

17. Интервальные оценки параметров распределения по эмпирическим данным.

18. Понятие о критерии согласия. Критерий Пирсона хи-квадрат.

19. Статистическая и корреляционная связь. Уравнения прямых регрессий.

1. Основные понятия теории вероятностей

Вся практическая деятельность человека может рассматриваться как совокупность неких событий. Часть событий вполне закономерна и предсказуема. Но существуют события, которые невозможно заранее предсказать. Все события можно разделить на следующие основные виды:

случайное событие – это событие, которое может произойти или не произойти при осуществлении определенной совокупности условий. Таким образом, реализацию случайного события нельзя предсказать заранее (при одних и тех же условиях). Эти условия часто задаются условиями проведения опыта или испытания, поэтому случайное событие часто есть результат испытания;

достоверное событие – это событие, которое всегда происходит при определенных условиях;

невозможное событие – это событие, которое никогда не происходит при данных условиях;

несовместные события – это случайные события, которые при данных условиях не могут произойти совместно;

независимые события – это случайные события, которые при данных условиях происходят независимо друг от друга. В противном случае, события называются зависимыми;

равновозможные события – это события, возможности появления которых при данных условиях одинаковы. Набор (или группа) событий называется полным, если при данных условиях всегда реализуется хотя бы одно из этих событий.

Полный набор несовместных и равновозможных событий называется набором элементарных событий или исходов; а их совокупность } – вероятностным пространством элементарных событий. Такая схема описания ситуации называется классической и является основной.

Элементарные события (исходы), при реализации которых происходит событие A, называются благоприятными для A.

Относительная частота события. При большом числе испытаний, проведенных в одних и тех же условиях, можно установить закономерность появления некоторого события A. Пусть при проведении n₁ испытаний событие A наступило m₁ раз. Тогда частное m₁/n₁ есть относительная частота события A.

Можно продолжить серии испытаний и найти, что в n₂ испытаниях событие A наступило m₂ раз, тогда относительная частота этого события составит m₂/n₂ и т.д. В результате получим последовательность относительных частот m₁/n₁, m₂/n₂, m₃/n₃, … , m_i/n_i, … , заметив при этом, что отношения m_i/n_i, i = 1,2,3,…, мало отличаются друг от друга при большом числе одинаковых и независимых испытаний. Таким образом, относительная частота случайного события устойчива при большом числе испытаний и колеблется относительно некоторого предельного значения – предельной частоты , которая может служить объективной количественной мерой возможности реализации случайного события или вероятностью события.

Вероятность события A обозначается P(A).

Вероятность события в классической схеме определяется как отношение числа m элементарных исходов, благоприятных событию A, к общему числу n исходов вероятностного пространства:

.

По теореме Бернулли .

Свойства классической вероятности: вероятность события A не может быть меньше нуля и больше единицы (0 ≤ P(A) ≤ 1); вероятность невозможного события равна нулю, вероятность достоверного события равна единице.

Геометрическое определение вероятности основано на взаимно-однозначном сопоставлении пространству точек некоторой области и используется, когда множество элементарных исходов несчетно. В этом случае вероятность принимается равной относительной мере той части области (длине, площади, объему и т.д.), которая соответствует благоприятным событию исходам. Так, если геометрическая мера всей области равна S, а геометрическая мера части этой области, попадание в которую благоприятствует событию A, равна S_A, то вероятность события A:

.

При непосредственном подсчете вероятностей событий часто необходимы сведения из комбинаторной математики. Эта область математики занимается, в основном, задачами о существовании и подсчете различных комбинаций (выборок), которые можно составить из элементов данного конечного множества.

Факториал  произвольного целого числа определяется формулами: .

Перестановками из n различных элементов называются выборки, содержащие все n элементов и различающиеся только порядком элементов. Число перестановок из n элементов P_n = n! Например, P₄ = 4! = 1  2  3  4 = 24.

Размещениями по m элементов из n различных элементов (m ≤ n) называют выборки по m элементов, которые отличаются одна от другой составом элементов или порядком их расположения. Число размещений по m элементов из n:

.

Сочетаниями по m элементов из n различных элементов называются выборки, отличающиеся только составом самих элементов. Число таких сочетаний находится по формуле:

.

Пример 1. Игральную кость бросают один раз. Найти вероятность появления четного числа очков.

Решение. При подбрасывании одной игральной кости пространство элементарных событий (число выпавших очков) состоит из шести исходов: 1, 2, 3, 4, 5, 6}. Пусть A – событие, состоящее в появлении четного числа очков. В этом случае событию А благоприятствуют исходы выпадения 2, 4, 6 очков, т.е. n = 6, m = 3. тогда

.

Пример 2. В ящике пять белых и четыре черных шара. Из ящика вынимают три шара. Какова вероятность того, что эти шары белые? Какова вероятность того, что один шар белый?

Решение. Пусть событие A состоит в извлечении трех белых шаров. Общее число исходов (столько различных выборок по три шара можно составить из имеющихся в ящике девяти шаров). Число m исходов опыта, благоприятных A, равно ( ), так как столько различных выборок по три шара можно составить из имеющихся пяти белых шаров.

Тогда

.

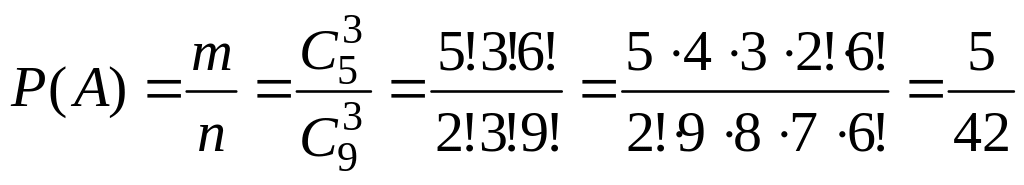Пусть событие B состоит в извлечении трех шаров, один из которых – белый. Этот шар можно вынуть способами из пяти белых, а оставшиеся 3 – 1 = 2 шара выборки можно вынуть способами из четырех черных шаров. Тогда число выборок, благоприятных B, определяется комбинированием всех этих способов заполнения выборки, т.е. . Откуда

.

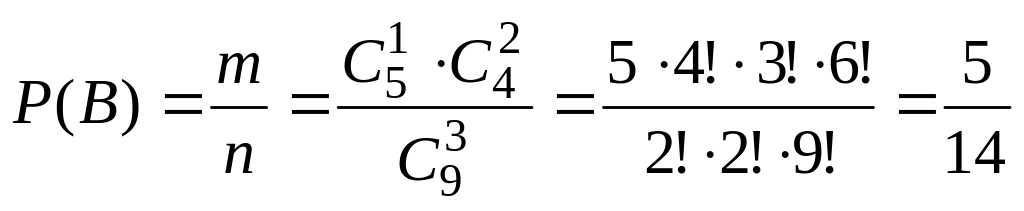Суммой A + B двух случайных событий A и B называется событие, состоящее в появлении события A или события B, или обоих этих событий.

Произведением AB двух событий A и B называется событие, состоящее в совместном появлении события A и события B.

Противоположным по отношению к событию A называется событие  , происходящее всегда, когда не происходит A.

Вероятность суммы совместных событий

.

Если события A и B несовместны, то P(AB) = 0, следовательно,

.

Так как противоположные события несовместны и образуют полную группу, то сумма их вероятностей

.

Условное событие A/B – это событие A при условии, что событие B уже произошло.

Вероятность произведения событий

,

где P(A/B) и P(B/A) – вероятности условных событий.

Если события A и B независимы, , и имеет место формула

.

Пример 3. Разрыв электрической цепи происходит при выходе из строя двух элементов A и B или двух элементов C и D. Найти вероятность разрыва цепи, если элементы выходят из строя независимо друг от друга с вероятностями 0,3 и 0,6, 0,4 и 0,5 соответственно.

Решение. Если события A, B, C, D – выход из строя соответствующих элементов, то по определению произведения и суммы событий согласно условию задачи разрыв цепи есть событие .

События A, B, C, D независимы, но могут быть совместными, и следовательно,

.

Пример 4. Два стрелка попадают в мишень с вероятностями соответственно 0,6 и 0,8. Какова вероятность того, что после залпа в мишени будет одна пробоина? Какова вероятность, что в мишени будет хотя бы одна пробоина?

Решение. Если – попадание первого стрелка, – попадание второго стрелка, то после залпа (совместная стрельба) в мишени будет одна пробоина от кого-то одного и промаха другого стрелка, т.е. , где слагаемые, очевидно, несовместны, а попадания или промахи стрелков независимы. Поэтому, используя формулу вероятности противоположного события, получим

.

Пусть событие B = (хотя бы одна пробоина); тогда противоположное ему событие  = (ни одной пробоины), т.е.  =  . Так как , то .

Формула полной вероятности. Формула Байеса. Вероятность события А, которое может произойти при наступлении одного из несовместных событий (гипотез) H₁, H₂, …, H_n, образующих полную группу событий , вычисляется по формуле

P(A) = P(H₁)P(A/H₁) + P(H₂)P(A/H₂) + … + P(H_n)P(A/H_n),

где P(H_i) – вероятность события H_i; P(A/H_i) – условная вероятность события A при наступлении события H_i, i = 1, 2, …, n.

Полученная формула для P(A) называется формулой полной вероятности и применяется при наличии полной группы несовместных событий.

С формулой полной вероятности тесно связана формула Байеса. Если до проведения опыта вероятности (априорные) гипотез были P(H₁), P(H₂), …, P(H_n), а в результате опыта событие A произошло, то с учетом этого «новые», т.е. условные вероятности (апостериорные) гипотез, вычисляются по формуле

,

где .

С помощью формулы Байеса возможно «пересмотреть» вероятность гипотез с учетом полученного (известного) результата опыта.

Пример 5. Имеются два ящика с шарами. В первом ящике шесть белых и четыре черных шара, во втором ящике десять белых и пять черных шаров. Из первого ящика во второй, неглядя, перекладывается один шар. После этого из второго ящика берут один шар. Найти вероятность того, что этот шар будет белым.

Решение. Пусть событие A – появление белого шара из второго ящика при гипотезах: H₁ – из первого ящика во второй переложен белый шар, H₂ – из первого ящика во второй переложен черный шар. Вероятности гипотез H₁ и H₂ равны вероятности извлечения из первого ящика одного белого или одного черного шара соответственно:

P(H₁) = 6/10 = 3/5, P(H₂) = 4/10 = 2/5.

После того, как во второй ящик из первого переложен один шар, количество шаров во втором ящике увеличится на единицу и станет равным 16. При перекладывании белого шара из первого ящика число белых шаров во втором ящике станет равным 11, а при перекладывании черного шара число белых шаров во втором ящике останется прежним. Тогда условные вероятности извлечения белого шара после перекладывания из второго ящика следующие: P(A/H₁) = 11/16, P(A/H₂) = 10/16. Искомая вероятность:

P(A) = P(H₁)P(A/H₁)+P(H₂)P(A/H₂) =

= 3/511/16+2/510/16 = 53/80.

Пример 6. На трех станках производятся одинаковые детали, причем на первом станке производят 25 %, на втором 35 %, на третьем 40 % всех деталей. В продукции трех станков брак составляет 5, 4 и 2 % соответственно. Все детали поступают на склад.

Найти вероятность того, что случайно выбранная деталь окажется бракованной.

Случайно взятая на складе деталь оказалась бракованной. Какова вероятность, что она изготовлена на первом станке

Решение. Пусть событие A – выбор бракованной детали. Есть три гипотезы: H₁ – деталь изготовлена на первом станке; H₂ – деталь изготовлена на втором станке; H₃ – деталь изготовлена на третьем станке.

По условию вероятности этих гипотез P(H₁) = 0,25, P(H₂) = 0,35, P(H₃) = 0,40. Условные вероятности события A – вероятности появления бракованной детали в продукции первого, второго или третьего станков: P(A/H₁) = 0,05, P(A/H₂) = 0,04, P(A/H₃) = 0,02. Тогда:

а) вероятность события A находим по формуле полной вероятности:

P(A) = P(H₁)P(A/H₁)+P(H₂)P(A/H₂)+P(H₃)P(A/H₃) = 

= 0,250,05+0,350,04+0,400,02 = 0,0345;

б) вероятность изготовления на первом станке находим по формуле Байеса:

.