8. Двойственные задачи лп

Рассмотрим следующую задачу. Пусть мебельная мастерская производит столы и шкафы из древесины 1, 2 или 3-го сорта. Расход материалов и их запасы следующие:

древесина	1	2	3
на 1 стол	0,15	0,2	0,05
на 1 шкаф	0,3	0,1	0,25
запас, м^3	60	40	50

Цена одного стола 12 условных единиц, а цена одного шкафа 15 условных единиц. Если – количество производимых столов и – количество производимых шкафов, то план производства и получаем задачу ЛП по оптимизации дохода .

в матричном виде

, , ,

где 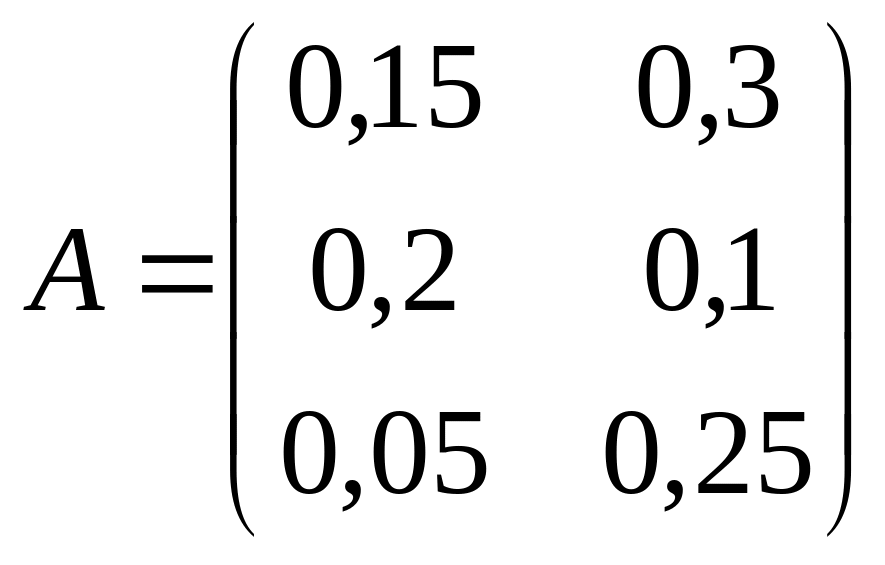, , , она является стандартной задачей ЛП.

Владельцу мастерской предложили продать древесину (без изготовления мебели). Пусть , и – цена 1 м³ древесины соответственно 1, 2 и 3-го сорта. Чтобы продавец не потерял своего дохода от продажи древесины, стоимость древесины, расходуемой на один стол и один шкаф, должна быть не меньше продажной цены древесины этих изделий:

(3)

где .

В интересах покупателя стоимость всей древесины необходимо минимизировать:

. (4)

Таким образом, получили двойственную задачу ЛП (3), (4), в которой максимум заменился на минимум, знаки неравенства изменились на противоположные, столбцы ограничений перешли в соответствующие по порядку строки, правые части ограничений (ресурсы) стали соответствующими по порядку коэффициентами целевой функции и, обратно, коэффициенты целевой функции стали ресурсами, причем число ограничений одной задачи равно числу переменных в другой.

В матричном виде такая взаимная двойственность между задачами ЛП описывается следующим образом:

где – транспонированная матрица А (столбцы становятся на место строк в соответствующем порядке). При этом за счет смысловых ограничений выполняются неравенства:

.

Теорема (о минимаксе). Если одна из двойственных задач разрешима, то разрешима и другая, причем экстремальные значения целевых функций обеих задач равны .

Следствие. Спрос и предложение могут уравновешиваться (возможно равновесие рынка).

Теорема (соотношения двойственности).

1. Если оптимальный план одной из двойственных задач удовлетворяет некоторому ограничению как строгому неравенству, то соответствующая (по номеру ограничения) переменная в оптимальном плане двойственной задачи равна нулю.

2. Если в оптимальном плане двойственной задачи какая-то компонента больше нуля, то соответствующее ограничение исходной задачи выполняется как равенство для ее оптимального плана.

Пример 23. Рассмотрим двойственные задачи ЛП:

;

Вторую задачу с двумя переменными легко решить (например, графически на плоскости) и получить оптимальный план . Так как первым трем ограничениям этот план удовлетворяет как строгим неравенствам, то по первому соотношению двойственности в оптимальном плане двойственной задачи (первой задачи) имеем . Так как в оптимальном плане второй задачи, двойственной к первой задаче, первая компонента , то по второму соотношению двойственности первое ограничение первой задачи выполняется как равенство . Следовательно, оптимальный план первой задачи и при этом .

Компоненты оптимального плана двойственной задачи называются оценками (или объективно обусловленными ценами) и по соотношениям двойственности показывают, какие ресурсы исходной задачи исчерпываются, а какие – нет. Кроме того, с помощью этих оценок можно выяснить как изменяется значение целевой функции исходной задачи при изменении ресурсов . В силу линейности функций

.

Отсюда следует, что .

Приращение целевой функции

Таким образом, зная оптимальное значение , можно определить оптимальное значение и для изменившихся значений ресурсов.