
- •Введение
- •1. Основные понятия теории вероятностей
- •2. Повторение незавИсИмых опытов
- •3. Случайные величины и их числовые характеристики
- •4. Система двух случайных величин и регрессия
- •Закон распределения двумерной случайной величины
- •5. Основы математической статистики
- •Контрольная работа 4
- •Задача 2.
- •Контрольная работа 5
- •6. Линейное программирование. Основные понятия и экономическая интерпретация
- •6.1. Задача лп
- •6.2. Примеры постановки задач лп
- •6.3. Геометрическая интерпретация задачи лп. Графическое решение
- •6.4. Основные формы задачи лп
- •6.5. Симплексный метод и приведение задачи лп к правильной форме
- •6.6. Признаки оптимальности начального допустимого плана
- •7. Метод искусственного базиса
- •8. Двойственные задачи лп
- •9. Транспортная задача и метод потенциалов
- •Контрольная работа 6
- •Рекомендательный библиографический список
- •Значения в зависимости от числа степеней свободы m и уровня значимости ( – доверительная вероятность)
- •Содержание
6.4. Основные формы задачи лп
Задача минимизации ЛП, для которой все ограничения являются равенствами с неотрицательными ресурсами и смысловыми ограничениями, называется канонической задачей.
Каноническая задача имеет вид
![]() ,
,
![]() ,
,
![]() (
(![]() и
и
![]() ).
).
Любую задачу ЛП можно свести к канонической форме, если использовать следующие приемы:
1) ![]() ,
т.е. свести задачу максимизации к задаче
минимизации;
,
т.е. свести задачу максимизации к задаче
минимизации;
2) за счет изменения знака или представления переменной разностью двух новых неотрицательных переменных можно добиться выполнения смысловых ограничений.
если
![]() ,
то
,
то
![]() ,
а если знак переменной
,
а если знак переменной
![]() неизвестен (например, может меняться!),
то
неизвестен (например, может меняться!),
то
![]() ,
где
,
где
![]() ,
,
![]() ;
;
3) за счет изменения знака в обеих частях ограничений можно получить все ресурсы ;
4) за счет прибавления или вычитания в левой части неравенства неотрицательных дополнительных (балансирующих) переменных можно сделать все ограничения равенствами.
Пример 17. Привести к канонической форме задачу ЛП
![]() ,
,
![]()
Решение.
Имеем
![]() ;
;
![]()
где
![]() ,
,
![]() и
и
![]() – дополнительные (балансирующие)
переменные и коэффициенты целевой
функции
– дополнительные (балансирующие)
переменные и коэффициенты целевой
функции
![]() = (3,
1, –1, 1, 0, 0, 0),
= (3,
1, –1, 1, 0, 0, 0),
![]() .
Матрица ограничений
.
Матрица ограничений

состоит из столбцов коэффициентов
ограничений при соответствующих
переменных
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
;
вектор ресурсов
,
,
,
;
вектор ресурсов
![]() .
.
Канонические
задачи ЛП удобно записывать в виде
расширенной матрицы, если представить
целевую функцию равенством, аналогичным
равенствам ограничений:
![]() и поместить это равенство в дополнительную
строку. Таким образом, расширенная
матрица канонической задачи ЛП
и поместить это равенство в дополнительную
строку. Таким образом, расширенная
матрица канонической задачи ЛП
![]() ,
,
![]() ,
имеет вид
,
имеет вид
![]() .
.
В частности, для примера 17 имеем расширенную матрицу
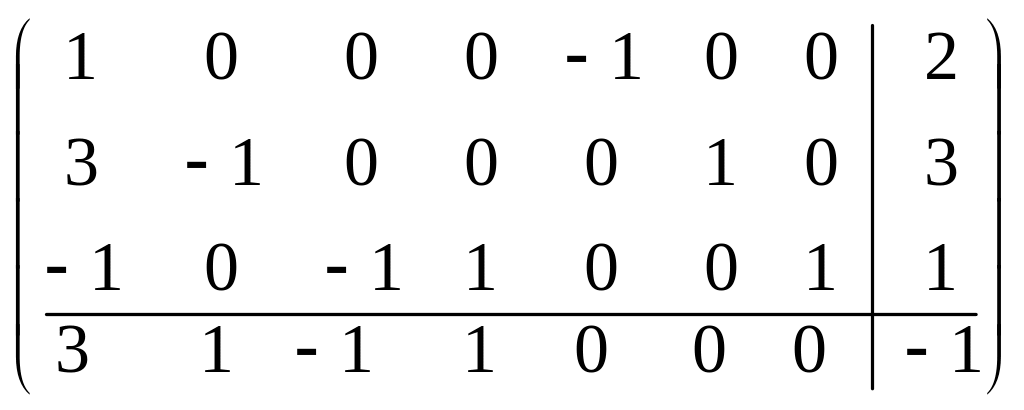 .
.
Рассмотрим каноническую задачу
ЛП в матричном виде. Пусть в матрице
ограничений А имеется максимальное
число различных столбцов, состоящих из
одной единицы и нулей (правильные или
базисные столбцы). Такие правильные
столбцы линейно независимы и поэтому
их число
![]() .
Если элементарными преобразованиями,
например методом Гаусса, получить нули
под этими правильными столбцами матрицы А
и в дополнительной строке расширенной
матрицы, т.е. исключить соответствующие
переменные из целевой функции (получить
правильные столбцы в расширенной
матрице), то полученная форма задачи ЛП
является правильной или базисной. Таким
образом, расширенная матрица правильной
задачи, с точностью до перестановки
столбцов, имеет вид
.
Если элементарными преобразованиями,
например методом Гаусса, получить нули
под этими правильными столбцами матрицы А
и в дополнительной строке расширенной
матрицы, т.е. исключить соответствующие
переменные из целевой функции (получить
правильные столбцы в расширенной
матрице), то полученная форма задачи ЛП
является правильной или базисной. Таким
образом, расширенная матрица правильной
задачи, с точностью до перестановки
столбцов, имеет вид
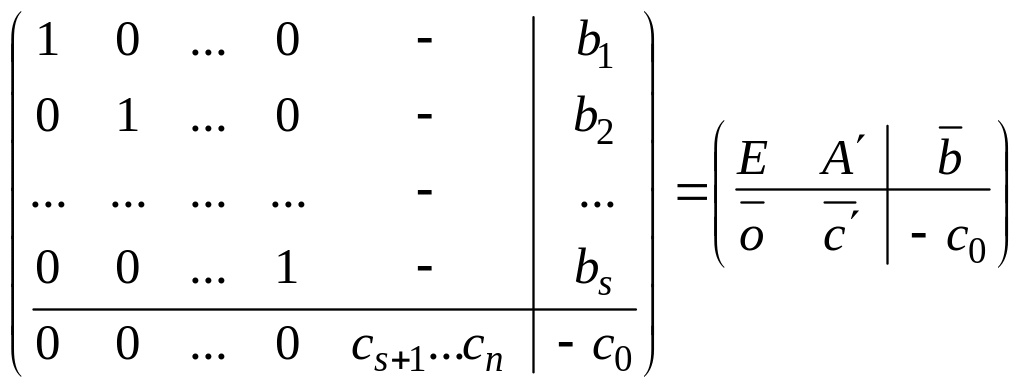 ,
,
где
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
Переменные, соответствующие правильным
столбцам, называются базисными (
.
Переменные, соответствующие правильным
столбцам, называются базисными (![]() ),
а остальные переменные – свободными
(
),
а остальные переменные – свободными
(![]() ).
В правильной задаче базисные переменные
выражаются через свободные
).
В правильной задаче базисные переменные
выражаются через свободные
![]() ,
(2)
,
(2)
и в целевую функцию входят
только свободные переменные. В правильной
задаче ЛП легко выписать начальный
допустимый план, если взять свободные
переменные равными нулю:
![]()
![]() .
Тогда по (2)
.
Тогда по (2)
![]() ,
,
![]() ,
…,
,
…,
![]() .
Базисные переменные
равны правым частям (ресурсам), стоящим
напротив единицы в соответствующем
правильном столбце. Таким образом,
начальный допустимый план
.
Базисные переменные
равны правым частям (ресурсам), стоящим
напротив единицы в соответствующем
правильном столбце. Таким образом,
начальный допустимый план
![]() .
При этом значение
целевой функции
.
При этом значение
целевой функции
![]()
![]() .
.
Следствие 1. В правильной задаче ЛП ограничения всегда совместны.
Следствие 2. Так
как нулевые значения свободных переменных
вектора
![]() являются крайними, то геометрически
начальный допустимый план соответствует
некоторой крайней точке симплекса
(некоторой его вершине).
являются крайними, то геометрически
начальный допустимый план соответствует
некоторой крайней точке симплекса
(некоторой его вершине).
