9. Транспортная задача и метод потенциалов
Одной из основных задач ЛП является транспортная задача. Она формулируется следующим образом.
в
пунктах
производится некоторый продукт. Этот
продукт следует доставить в пункты
.
В пункте
производится количество продукта
,
а потребность пункта
равна количеству продукта
.
Обозначим стоимость перевозки единицы
продукта из
в
через
.
Тогда транспортные расходы задаются
матрицей стоимостей
.
Если
– количество продукта, перевозимого
из
в
,
план перевозок задается матрицей
.
И для данного плана
суммарные транспортные расходы
.
Эту целевую функцию следует минимизировать
при условиях удовлетворения потребностей
для любого пункта потребления
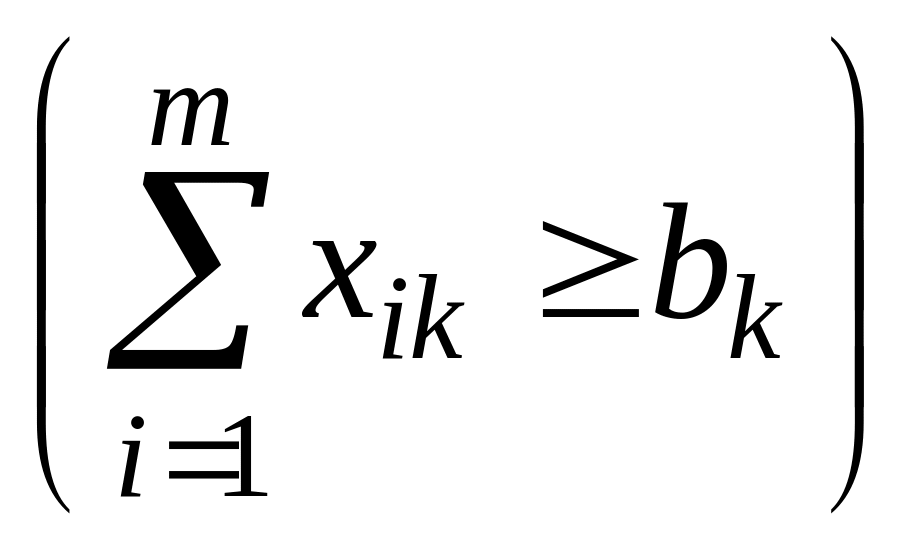и непревышения производства при вывозе
из любого пункта производства
.
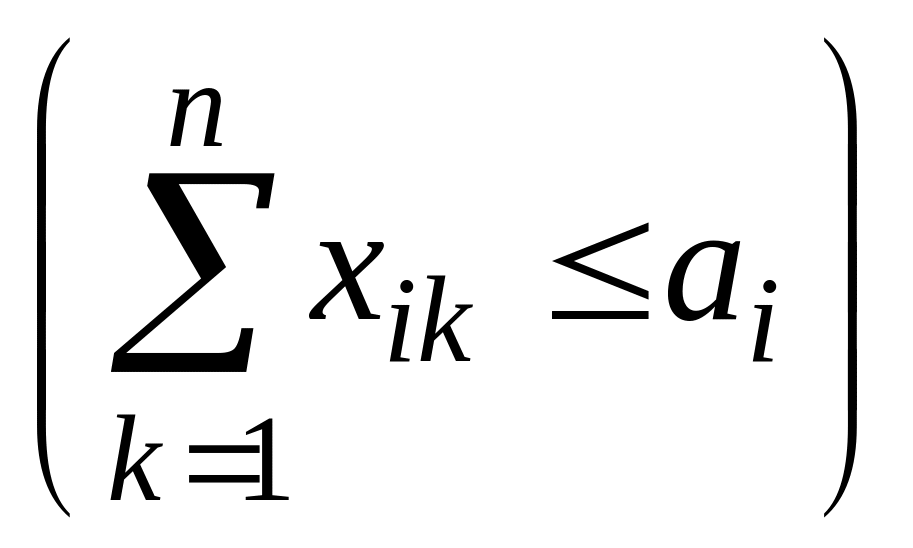Таким образом, получили транспортную
задачу:
;
;
(
,
),
где
.
Для
возможности решения такой задачи
необходимо выполнение условия
Во всех ограничениях
ставят знак равенства, потому что
излишний продукт (запас) можно складывать
и никуда не перевозить, т.е. получим
уравнений для
неизвестных. Задача имеет смысл при
,
что заведомо выполнено для
и
.
Таким
образом, транспортная задача в стандартной
записи:
,
,
(
,
),
где
;
.
Такие
ограничения достаточно просто привести
к правильной форме, хотя и громоздко в
силу большого числа переменных. При
этом в силу равенства
число базисных переменных на единицу
меньше числа уравнений, т.е. равно
.
Для такой задачи легко построить
начальный допустимый план (ограничения
всегда совместны), например по методу
наименьшей стоимости ввести перевозки,
обеспечивающие потребности с меньшей
стоимостью. Отметим, что данные задачи
удобно записывать в виде следующей
таблицы:
,
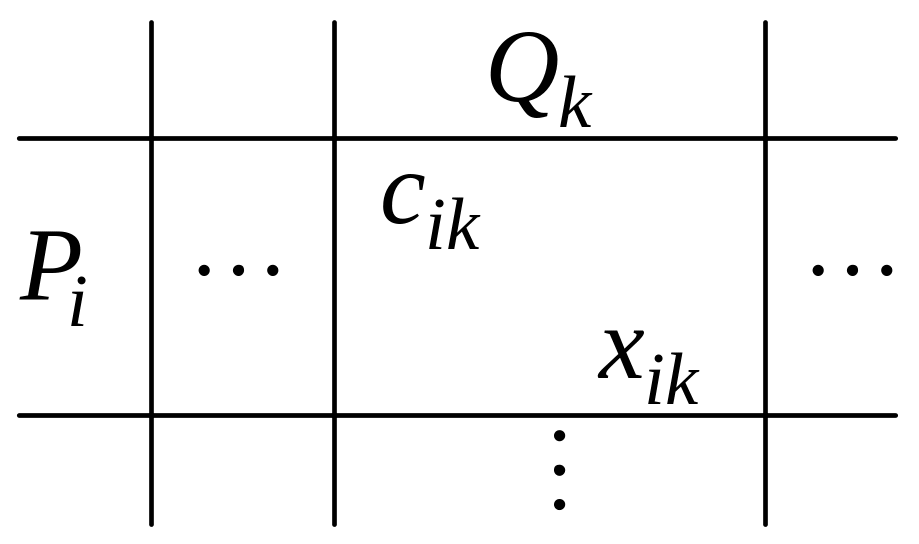где
– стоимость;
– величина перевозки.
Пример 24. Построить начальный допустимый план для данных задачи (табл.9) (т = 3, п = 4).
Таблица 9
|
|
|
|
|
|
|
1 |
2 |
3
6 |
4
|
6 |
|
4 |
3 |
2
2 |
0
6 |
8 |
|
0
4 |
2
6 |
2
0 |
1 |
10 |
|
4 |
6 |
8 |
6 |
= 24 |
Решение.
Возьмем клетку
,
т.е. (3, 1), с нулевой стоимостью
и перевезем из
,
где
,
весь необходимый для
продукт
(
)
и заполним клетку (3, 1). Итак, первый
столбец (
)
закрыт. Возьмем клетку (2, 4), где
,
и закроем потребность
(
)
перевозкой
из
,
где
,
т.е. заполним клетку (2, 4). Итак, столбец
закрыт. Оставшиеся в
2 единицы продукта переведем в
,
где стоимость
– наименьшая в строке
(
),
и строка
закрыта. В строке
остались клетки для
и
,
где
,
и поэтому удобно оставшиеся в
6 единиц продукта вывезти в
(
)
и закрыть
.
Осталось вывезти из
6 единиц продукта в
(
)
и закрыть последние
и
.
Получилось пять
базисных переменных (базисных клеток),
а необходимо иметь
базисных переменных. Поэтому добавим
одну базисную переменную с нулевой
перевозкой, например, положим
в клетке (3, 3). Транспортные расходы
по этому начальному плану
.
Отметим, что если производство
для какого-то пункта
или потребность
для какого-то пункта
,
то их можно не рассматривать, вычеркнуть
соответственную строку
или столбец из таблицы данных и уменьшить
размеры задачи (сделав задачу
невырожденной!).
Базисные клетки, где расположены базисные переменные, называются опорными.
Транспортную задачу можно
решать обычным симплексным методом, но
в силу большого числа переменных гораздо
проще решать специальными методами,
например методом потенциалов. Для
каждого пункта введем потенциалы:
для
и
для
,
чтобы для опорных клеток:
.
Таким образом, мы имеем
линейное уравнение для
потенциалов.
Эту систему уравнений легко решать,
если выбрать какое-нибудь «начальное»
значение потенциала, например
.
Определим для всех остальных, т.е.
свободных, клеток
псевдостоимость
и косвенную стоимость
,
которая является коэффициентом при
соответствующей свободной переменной
в целевой функции правильной формы этой
транспортной задачи. Следовательно,
если есть косвенная стоимость
,
то этот допустимый план не оптимален
(теорема 2, п.1). Выбираем самый большой
отрицательный коэффициент (косвенную
стоимость)
и образуем цикл пересчета плана, начиная
с этой клетки
с вершинами в каких-то опорных клеток,
проходимых по одному разу. Меняем каждый
раз направление в вершине на 90,
т.е. со строки переходя в столбец и
обратно. Так как вершин в цикле всегда
четное число, то в каждой клетке цикла
запишем величину пересчета
с чередующимися знаками:
или
,
начиная с
в начальной вершине цикла в клетке
.
Выбираем наибольшую величину
так, чтобы не нарушить смысловые
ограничения в тех клетках вершин цикла,
где стоит
,
т.е.
.
Эта величина
называется пересчетом цикла, а величина
– ценой цикла. Пересчитав план с
использованием
,
получим новый допустимый план, удалив
из опорных (базисных) клеток ту клетку
или одну из тех клеток, где новое значение
перевозки
.
Если величина транспортных
расходов по старому плану равна
,
то для нового плана расходы
.
Пример 25.
Для начального допустимого плана
перевозок, построенного в примере 24,
определим потенциалы
и
при
;
;
;
;
;
.
Из
этих уравнений находим потенциалы
;
;
.
Запишем потенциалы в новую таблицу, для которой определим псевдостоимости и косвенные стоимости (табл.10).
Таблица 10
|
|
|
|
|
|
1 0
1 |
2 –1 + 3 |
3 6-
|
4 3
1 |
|
4 4
0 |
3 1
2 |
2 2
|
0
6 |
|
0 4 |
2 6- |
2 0+
|
1 1
0 |
Тогда
для свободных клеток имеем псевдостоимости
,
которые записываем в левом нижнем углу
клетки:
;
;
;
;
;
.
Косвенные стоимости
запишем в правом верхнем углу клетки:
;
;
;
;
;
.
В
клетке (1; 2) имеем единственную
отрицательную косвенную стоимость
и поэтому образуем цикл пересчета,
начиная с этой клетки
,
чередуя знаки величины пересчета
(табл.10). В нашем случае пересчет цикла
.
Пересчитаем план по величине
и удалим одну лишнюю базисную переменную,
равную нулю (
).
Затем снова восстановим потенциалы
(
),
псевдостоимости и косвенные стоимости,
записав их в нужные углы клеток новой
таблицы (табл.11):
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
1.
Таблица 11
|
|
|
|
|
|
1 1
0 |
2 6
|
3 1
2 |
4 4
0 |
|
4 4
0 |
3 1
2 |
2 2
|
0
6 |
|
0 4 |
2 0 |
2 6
|
1 1
0 |
Все
косвенные стоимости новой таблицы
неотрицательны. Данный план перевозок
,
,
,
,
,
оптимален. Расходы по этому новому плану
.
Рис.8.
Цикл пересчета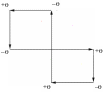
Замечание 2. Стороны цикла могут пересекаться, но точки пересечений не могут служить вершинами цикла (рис.8).
Замечание 3. Если удачно составлен начальный допустимый план, то оптимальность может достигаться сразу, без пересчета по циклам, что и устанавливается с помощью метода потенциалов.
Пример 26.
Пусть транспортная задача и ее начальный
допустимый план перевозок заданы
таблицей (табл.12),
в которую вписан начальный допустимый
план (
).
Решение. Расходы
по этому плану
.
Найдем потенциалы (при
):
;
;
;
;
;
;
,
,
,
,
,
,
.
Определим псевдостоимости и косвенные
стоимости для свободных клеток:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Таблица 12
|
|
|
|
|
аi |
|
6 2
4 |
2 2
0 |
3 0
3 |
1 5
|
5 |
|
5 1
4 |
0 10–
|
3 5+
|
5 4
1 |
15 |
|
5 6+
|
8 7
1 |
4 5–
|
2 5
|
16 |
|
9 4–
|
3 –2 + 5 |
6
8 |
8 6
|
4 |
bk |
10 |
10 |
10 |
10 |
= 40 |
Следовательно,
план не оптимален и поэтому образуем
цикл пересчета, начиная с клетки (4; 2)
(табл.13).
Пересчет цикла
.
Пересчитаем по величине
и удалим лишнюю базисную переменную
.
Затем снова восстановим потенциалы
(
),
псевдостоимости и косвенные стоимости,
записав их в нужные углы клеток:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Таблица 13
|
|
|
|
|
|
6 2
4 |
2 2
0 |
3
3 |
1 5
|
|
5 1
4 |
0 6
|
3 9
|
5 4
1 |
|
5 10 |
8 7
1 |
4 1
|
2 5
|
|
9 2
7 |
3 4 |
6 0
6 |
8
4 |
Все
косвенные стоимости неотрицательны и
данный план перевозок
,
,
,
,
,
,
оптимален. Расходы по этому плану
.