6. Линейное программирование. Основные понятия и экономическая интерпретация

Математическое программирование занимается построением алгоритмов или программ конструктивного решения задач оптимизации, т.е. задач на наибольшее или наименьшее значения функции нескольких переменных при заданных ограничениях. В общем виде такие задачи можно описать следующим образом:

,

т.е. максимизировать функцию при условии

или ;

,

т.е. минимизировать функцию при условии

или .

Оптимизируемая функция называется целевой, а область ограничений (или допустимое множество) является областью в многомерном евклидовом пространстве , векторы которого или имеют декартовых координат, а скалярное произведение определяется как , что аналогично обычному скалярному произведению в пространстве . В евклидовом пространстве , как и в трехмерном пространстве, определяются такие понятия, как базис, разложение по базису, свойство ортогональности и т.п. Так как аналитически области в задаются системами неравенств или равенств, то условие означает, что

,

где – некоторые заданные функции. При этом в ограничениях можно рассматривать только неравенства, так как равенство есть частный случай неравенств вида . Отметим что, если все неравенства нестрогие , тогда область будет замкнутой, т.е. содержащей все точки своей границы.

Если область ограничений непустая Ǿ), ограничена и замкнута, а целевая функция непрерывна, то по теореме Вейерштрасса задача оптимизации всегда имеет решение, т.е. существуют такие точки , для которых и . От­метим, что таких оптимальных точек может быть несколько (аль­тернативные решения), но оптимальное значение всегда одно.

При нарушении условий теоремы Вейерштрасса решение задачи оптимизации может не существовать.

6.1. Задача лп

Если целевая функция и все функции линейны, – это случай задачи линейного программирования. Если хотя бы одна из этих функций нелинейна, – это случай задачи нелинейного программирования. Стандартный метод решения задач оптимизации при большом числе переменных и ограничений неэффективен. Для конкретного вида задач, например задач ЛП, созданы эффективные специальные методы.

Задачу ЛП можно записать в следующем виде:

,

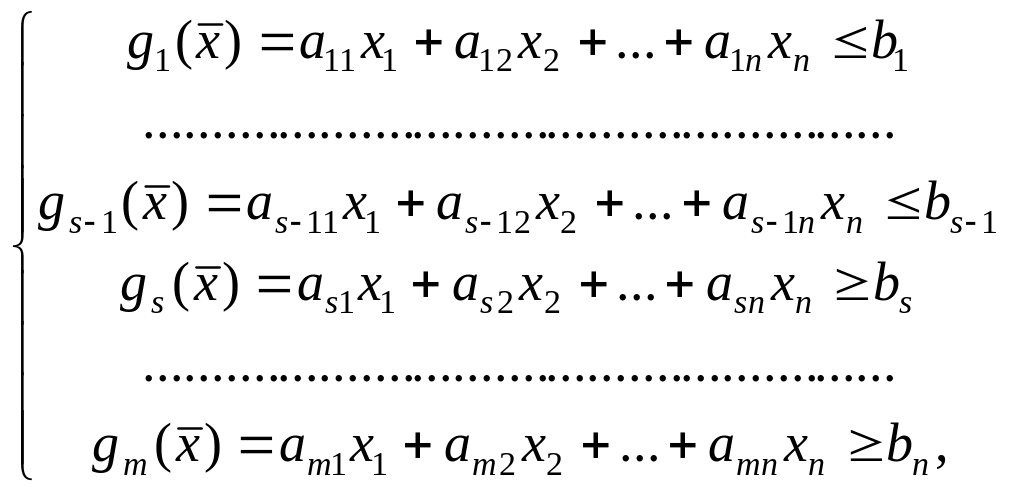
где .

Введем матрицу коэффициентов ограничений A и векторы переменных и правых частей :

, , .

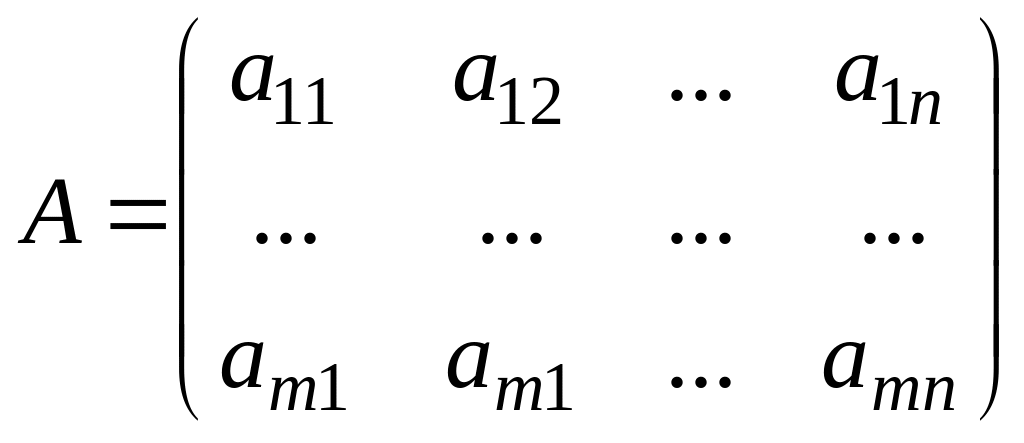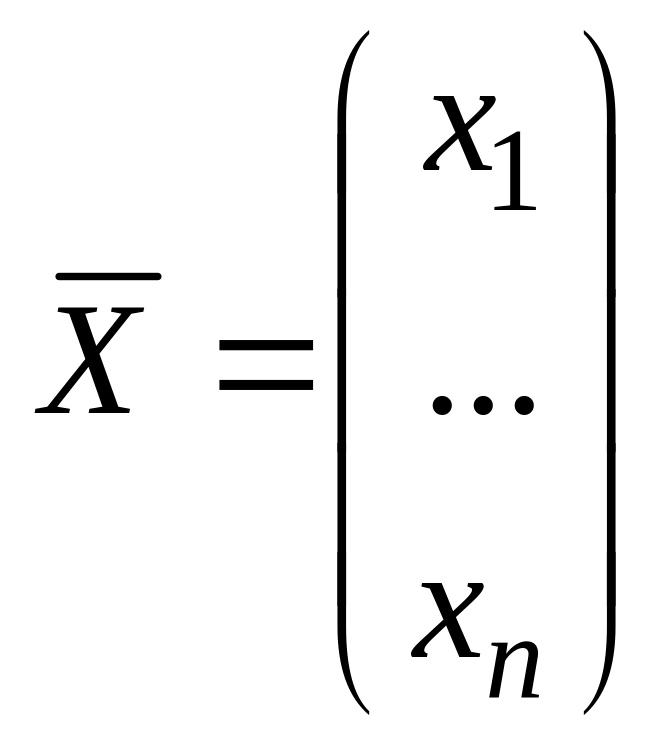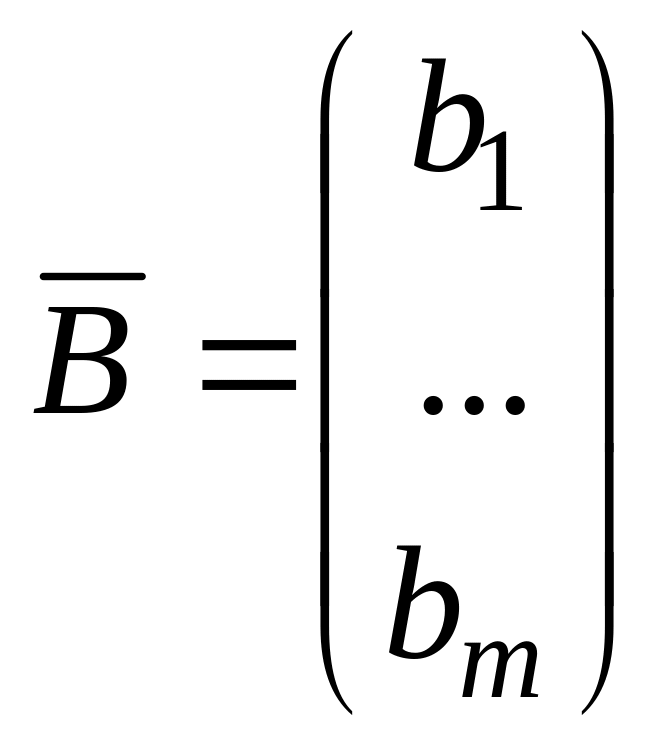За счет изменения знака в обеих частях приведем все неравенства к неравенствам одного вида и запишем систему ограничений в матричном виде: .

Так как

, (1)

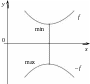
вместо задачи минимизации функции (рис.5) можно рассматривать максимизацию функции . Поэтому задачу ЛП всегда можно привести к стандартной форме: .

Рис.5. Максимизация

и минимизация функций

Экономические задачи оптимизации, связанные с планированием производства или распределением продуктов (изделий), являются задачами ЛП. Если рассматривать доходы, то это будут задачи максимизации, а если расходы – задачи минимизации. При этом значения переменных имеют смысл планируемого количества разных продуктов и являются неотрицательными: . В дальнейшем эти ограничения (смысловые) считаются выполненными. Если задача ЛП приведена к стандартной форме, то является вектором цен на соответствующие продукты, – постоянная составляющая дохода (или расхода), а целевая функция выражает величину дохода (расхода). Матрица ограничений является коэффициентом использования набора ресурсов, запасы которых заданы вектором ресурсов .

В силу такой экономической интерпретации вектор называется планом. При этот план допустимый. Если – допустимый план и , то этот план – оптимальный.

При непрерывности целевой функции и нестрогости всех ограничений (область ограничений замкнута) такая задача оптимизации может не иметь решения только в двух случаях:

1) область ограничений пуста:  Ǿ (ограничения несовместны);

2) целевая функция неограниченна на неограниченной области ( или ).