
- •1.Предмет теории вероятностей – анализ случайных явлений: отсутствие детерминистической регулярности и наличие статистической регулярности
- •2.Теория вероятностей как аксиоматизируемая математическая дисциплина
- •2. Эксперимент (опыт, испытание, явление)и его исход (результат, наблюдение)
- •3. Вспомогательная модель. Реализация этой идеи
- •4. Вероятностная модель
- •5. Вспомогательная и Вероятностная модели экспериментов. Однократное и двукратное подбрасывания монеты
- •7. Общая схема построения конечной вероятностной модели – вероятностного пространства
- •8. Произвели эксперимент, известен исход. Произошло ли событие?
- •9. Практическое значение вероятности события
- •11. Аксиомы а.Н. Колмогорова
- •1. Элементарная теория вероятностей
- •10. Необходимые в теории вероятностей сведения из теории множеств и теории меры
- •3. Основное определение
- •12. Непосредственные следствия из аксиом
- •13. Парадокс де Мере
- •14. Применения комбинаторного анализа в теории вероятности
- •2. Основное комбинаторное правило (частный случай)
- •3. Основное комбинаторное правило (общий случай)
- •15. Постановка комбинаторной задачи
- •16. Выборка с возвращением и без возвращения
- •17. Выборки неупорядоченные и упорядоченные
- •18. Упорядоченные выборки с возвращением
- •19. Упорядоченные выборки без возвращения-размещения
- •20. Перестановки
- •21. Неупорядоченные выборки из n элементов по k без возвращения – сочетания
- •24.Употребление термина «случайный» в теории вероятностей
12. Непосредственные следствия из аксиом
10.
сумма вероятностей всякого события
и его дополнения
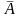 равно 1:
равно 1:
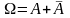
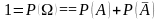 .
.
20.
если
- пустое множество, то
![]() .
На самом деле, полагая в 10 А = ,
получаем,
.
На самом деле, полагая в 10 А = ,
получаем,
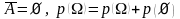 стало быть,
стало быть,
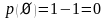 .
.
30.
если АА,ВА
и ВА,
то
 ,
в частности,
,
в частности,
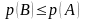 из ВА
следует А=В+(А\В), и поэтому
из ВА
следует А=В+(А\В), и поэтому
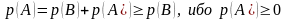
40.
если А,В А,
то
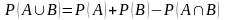 :
действительно,
:
действительно,
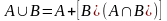 ,
откуда в силу 30,
имеем
,
откуда в силу 30,
имеем
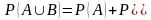 .
.
50.
Если А1,…,Аn
из А,
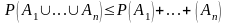
Положили
В1=А1,
при к2
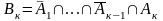 ,
тогда
,
тогда
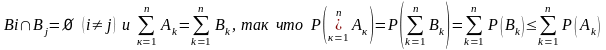
13. Парадокс де Мере
Де Мере заметил, что при бросании 3-х игральных костей 11 очков выпадает чаще, чем 12. Паскаль нашел решение этого вопроса. Ферма писал Паскалю: «Я вижу, что истина всегда одинакова: и в Париже, и в Тулузе». Де Мере считал так: 11 очков может выпасть следующими 6-ю способами:
(6-4-1), (6-3-2), (5-5-1), (5-4-2), (5-3-3), (4-4-3) (А)
12 очков: (6-5-1), (6-4-2), (6-3-3), (5-5-2), (5-4-3), (4-4-4) (В)
Де Мере не учитывал порядок, например, кроме (6-4-1) существует еще 5 вариантов: (6-1-4), (4-6-1), (4-1-6), (1-6-4), (1-4-6).
Итак: (6-4-1), (6-3-2), (5-5-1), (5-4-2), (5-3-3), (4-4-3), (А)
6 6 3 6 3 3
(6-5-1), (6-4-2), (6-3-3), (5-5-2), (5-4-3), (4-4-4). (В)
6 6 3 3 6 1
11
очков выпадает 6+6+3+6+3+3=27 способами, 12
очков- 6+6+3+3+6+1=25 способами, т.е. частота
выпадения 11 очков выше, следовательно
и вероятность
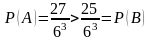 .
.
Весьма замечательным здесь является то обстоятельство, что результаты наблюдений привели к построению правильной математической модели.
Именно, пространство состоит из исходов =(а, в, с), где а, в и с есть число очков при первом , втором и третьем бросаниях соответственно.
Равенство =(а, в, с) =(а1, в1, с1)= (1) означает а=а1, в=в1, с=с1, а не а+в+с= а1+в1+с1, как полагал де Мере.
Другими словами, два исхода считаются разными, если различаются выпавшими очками или же, при совпадении выпавших очков, порядком их выпадения.
Ввиду «правильности» и «одинаковости» игральных костей, ни один исход не предпочтителен перед любым другим исходом, поэтому все исходы равновозможны, т.е. вероятность р() каждого исхода равна 1/N, где N - количество элементов в .
Поскольку при каждом бросании реализуется один из шести возможных случаев, то в трех бросаниях будет N=63=216 различных исходов (это строго доказано в следующем разделе).
И, наконец, пусть события А и В состоят в выпадении при трех бросаниях соответственно 11 и 12 очков: А={=(а,в,с): а+в+с =11} и В={=(а,в,с): а+в+с =12}.
Тогда
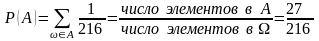 и
и
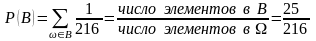
тем самым, вероятность выпадения 11 очков больше вероятности выпадения 12 очков, так что в длинной серии бросаний 11 очков выпадает чаще нежели 12 очков, что и заметил де Мере.
В
книге «Опыт
философии теории вероятности» Лаплас
рассказал об одном весьма примечательном
эпизоде, происшедшим с ним при изучении
закономерности рождения мальчиков и
девочек. Обширные статистические
материалы, изученные им для Лондона,
Петербурга, Берлина, всей Франции, давали
почти точно совпадающие отношения числа
рождений мальчиков к числу всех рождений.
Все эти отношения колебались в течение
десятилетий около одного и того же
числа, приблизительно равного 22/43. В то
же время исследование статистических
материалов аналогичного по Парижу за
40 лет (с 1745 по 1784 г.) приводило к иному
числу 25/49
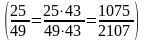 .
Лапласа заинтересовало столь значительно
различие, и он начал искать для него
рациональное объяснение. При детальном
изучении архивных материалов оказалось,
что в общее число рождений по Парижу
включались также все подкидыши. Выяснилось
далее, что окрестное население предпочитало
подкидывать преимущественно младенцев
одного пола. Само же явление социального
порядка в то время было настолько
распространенным, что существенно
исказило истинную картину рождаемости
в Париже. Когда Лаплас исключил из общего
числа рождений всех подкидышей, то
оказалось, что и для Парижа отношение
числа рождений также устойчиво и также
близко к числу 22/43
.
Лапласа заинтересовало столь значительно
различие, и он начал искать для него
рациональное объяснение. При детальном
изучении архивных материалов оказалось,
что в общее число рождений по Парижу
включались также все подкидыши. Выяснилось
далее, что окрестное население предпочитало
подкидывать преимущественно младенцев
одного пола. Само же явление социального
порядка в то время было настолько
распространенным, что существенно
исказило истинную картину рождаемости
в Париже. Когда Лаплас исключил из общего
числа рождений всех подкидышей, то
оказалось, что и для Парижа отношение
числа рождений также устойчиво и также
близко к числу 22/43
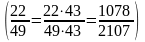 ,
как это имеет место для других народов
и для Франции в целом.
,
как это имеет место для других народов
и для Франции в целом.
Здесь мы имеем с совершенно другим и одинаково замечательным фактом, когда наблюдения (но не эксперименты) приводят к доказательству наличия статистической регулярности.
Более того, на основании статистических данных определяется вероятность, события, состоящего в «рождение мальчика», в то время как пространство элементарных событий двуэлементно:1= «рождение девочки» и 2= «рождение мальчика».
Все это составляет первый пример из математической статистики, когда вероятности определяются из известных статистических данных или же из постановок статистических экспериментов (что само по себе тоже просто, представляет отдельную науку).
Заметим, что более поздние статистические данные также приводят к выводу «вероятность рождения мальчика равна 0,514», т.е. на тысячу рождений ребенка 514 приходится мальчиков.
Вот
данные по Швейцарии с 1871 по 1900 годы:
n=2644757,
среди них n1=1359671
мальчиков, частота рождения мальчика
равна
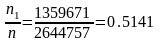 .
.
Итак,
вероятностная модель есть пространство
(
,А,
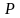 )
рождения ребенка, где :1=
«рождение девочки», 2=
«рождение мальчика».
)
рождения ребенка, где :1=
«рождение девочки», 2=
«рождение мальчика».
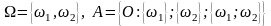 ,
,
 .
.
Серия
наблюдений в Лондоне , в Петербурге, в
Берлине, всей Франции, Париже (после
уточнения наблюдений Лапласа), Швейцарии
показывает, что частота события
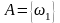 группируется
около вероятности
группируется
около вероятности
 .
.
