3. Основное комбинаторное правило (общий случай)

Начнем со следующей задачи. Номер автомобиля состоит из трех цифр и еще четырех букв латинского алфавита, если автомобиль личного пользования, и трех букв - в остальных случаях.

Сколько всего существует различных автомобильных номеров в каждом из этих случаев?

Такого типа задачи могут быть решены применением Основного комбинаторного правила, которое заключается в следующем:

Пусть дано натуральное число s и необходимо выполнить последовательно – одно за другим – s действий.

Если первое действие выполнимо n₁ способами,

второе действие выполнимо n₂ способами,

…………………………………………

последнее s – ое действие выполнимо n_s способами,

тогда все s последовательных действий вместе выполнимы ровно 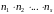способами.

Убедимся в справедливости основного правила, понимая, для наглядности, действия как последовательное составление комбинаций элементов по одному из каждой из данных s групп.

Итак, имеется s групп элементов:

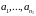- n₁ элементов первой группы,

- n₂ элементов второй группы,

…………………………….

- n_s элементов s – ой группы.

Требуется доказать, что общее количество разных комбинаций 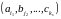есть .

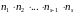При s=1 один элемент из одной группы из n₁ элементов выбирается, очевидно, n₁ способами: выбирая по одному за n₁ действий исчерпаем всю группу элементов.

При s=2 правило доказано в предыдущем пункте.

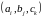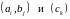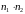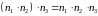При s=3 комбинации будем рассматривать как упорядоченные пары из – первых, по доказанному при s=2, комбинаций, вторых, очевидно, n₃, так что всего комбинаций. Тем самым, утверждение при s=3 доказано.

Применяя метод математической индукции, где переход от s к s+1 проводится дословным повторением приведенных рассуждений, убеждаемся в справедливости основного правила для произвольного s. Таким образом, основное комбинаторное правило доказано.

Применим это правило к сформулированной задаче о числе автомобильных номеров.

Номер автомобиля личного пользования состоит из последовательно выписанных: одной буквы латинского алфавита, трех цифр, и трех букв латинского алфавита, например,

1	2	3	4	5	6	7
Z	2	3	8	C	D	M

Латинский алфавит состоит из 26 букв, имеется 10 цифр.

Будем считать, что номер автомобиля личного пользования состоит из s=7 мест, где первое место-букву, можно заполнить любой из 26 букв латинского алфавита, т.е. n₁=26 способами, второе место-цифру, можно заполнить любой из цифр 0,1,…,9, т.е. n₂=10 способами, далее каждое третье, четвертое, пятое, шестое и седьмое место, n₃=10, n₄=10, n₅=26, n₆=26, n₇=26 способами соответственно.

Поэтому, согласно Основному комбинаторному правилу, всего имеется

N=n₁n₂n₃n₄n₅n₆n₇=26101010262626=456976000 автомобильных номеров.

В том же порядке рассуждений, номера остальных автомобилей можно выбрать

n₁n₂n₃n₄n₅n₆= способами.

д) «Размещение шаров по ящикам» состоит в выборе ящика для каждого шара. Если имеется r шаров, то для каждого ящика возможно r независимых исходов эксперимента, поэтому r шаров можно разместить по n ящикам n^r различными способами. Например, если грани игральной кости рассматривать как «ящики», предыдущее утверждение позволяет заключить, что при r-кратном бросании кости возможно 6 ^r различных исходов, из которых 5 ^r удовлетворяют условию «ни разу не выпало очко». Значит, в предположении, что все исходы опыта равновероятны, событие «при r бросаниях кости ни разу не выпало очко» имеет вероятность 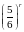. 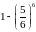Интуитивно можно рассчитывать, что при шести бросаниях «очко выпадает наверняка», но вероятность этого события равна только , или не менее .

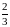Доказанное правило применяется также к решению других комбинаторных задач, к общей формулировке которой и переходим.