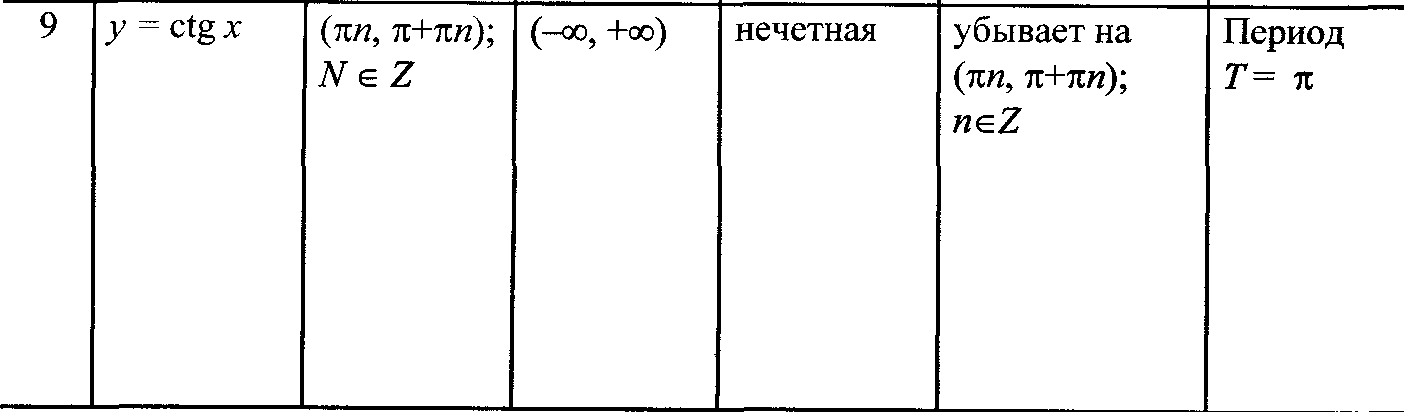
4. Тригонометрические функции

№ п/п	Обозначение функции	Область определения Х	Область значений Y	Четность, нечетность	Монотон­ность	Перио­дичность
6	у = sin х	(–, +)	[-1; 1]	нечетная	возрастает на [-/2+2n, /2+2n]; убы­вает на [/2+2n, З/2+2n], п  Z	Период T= 2л

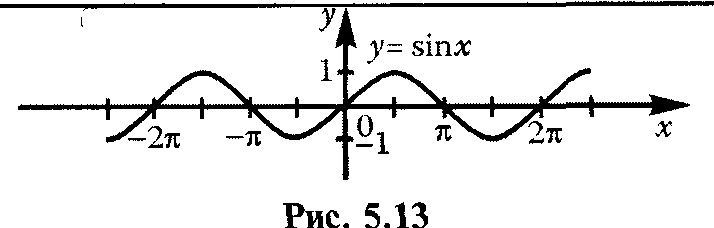
№ п/п

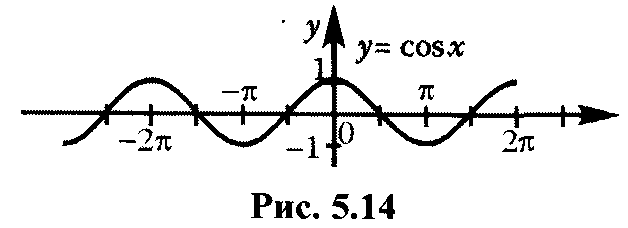
Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотон­ность

Перио­дичность

№ п/п

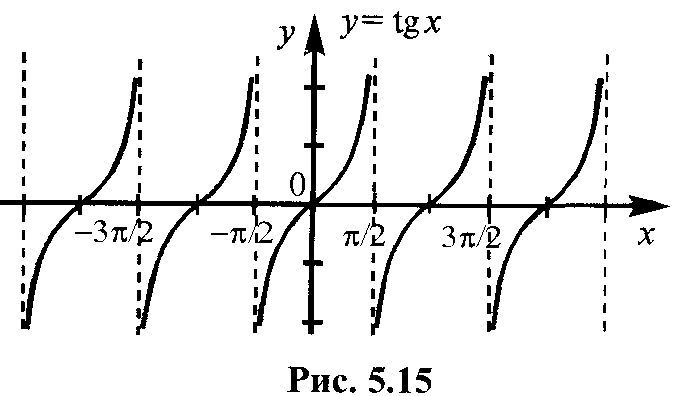
Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотон­ность

Перио­дичность

№ п/п

Обозначение функции

Область определения Х

Область значений Y

Четность, нечетность

Монотон­ность

Перио­дичность

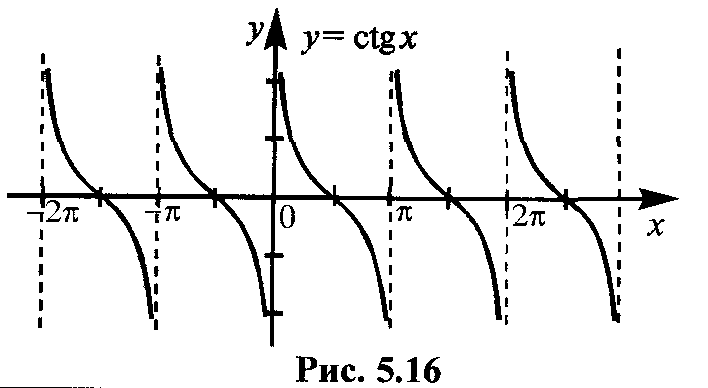
5. Обратные тригонометрические функции

у = arcsin х, у = arccos х, у = arctg х, у = arcctg x

4. Периодичность. Функция у = f (х) называется периодиче­ской с периодом Т  0, если для любых х из области определе­ния функции f(x+T)=f(x).

Например, функция у = sin х имеет период Т = 2, так как для любых х sin (х +2л) = sin х.

5.5. Элементарные функции. Классификация функций. Преобразование графиков

Функция называется явной, если она задана формулой, в ко­торой правая часть не содержит зависимой переменной; напри­мер, функция у = х² + 5х +1.

Функция у аргумента х называется неявной, если она задана уравнением F(х, у) = 0, не разрешенным относительно зависи­мой переменной. Например, функция у (у > 0), заданная урав­нением х³ + у² - х = 0. (Заметим, что последнее уравнение задает две функции

Обратная функция. Пусть у = f (х) есть функция от незави­симой переменной х, определенной на множестве Х с областью значений Y. Поставим в соответствие каждому у  Y единствен­ное значение х  X, при котором f(х) = у. Тогда полученная функция х =  (у), определенная на множестве Г с областью зна­чений X, называется обратной.

Так как традиционно независимую переменную обозначают че­рез х, а функцию через у, то функция, обратная к функции у =f(x), примет вид у =  (х). Обратную функцию у = (х) обозначают также в виде у = f^–1 (х) (аналогично с обозначением обратной величины).

Например, для функции у = a^х обратной будет функция х = log_a у или (в обычных обозначениях зави­симой и независимой переменных) у= log_ax.

Можно доказать, что для любой строго монотонной функции у = (х) существует обратная функция.

Графики взаимно обратных функций симметричны относи­тельно биссектрисы первого и третьего координатных углов (на рис. 5.17 показаны графики взаимно обратных функций у =a^x и у = log_a х при a > 1).

Сложная функция. Пусть функция у =f(u) есть функция от переменной и, определенной на множестве U с областью значе­ний Y, а переменная и в свою очередь является функцией и = (х) от переменной х, определенной на множестве Х с обла­стью значений U. Тогда заданная на множестве Х функция y = f[(x)] называется сложной функцией (или композицией функций, суперпозицией функций, функцией от функции).

Например, у = lg sin х – сложная функция, так как ее мож­но представить в виде у = lg и, где и = sin х.

Понятие элементарной функции. Из основных функций новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операций образования сложной функции.

Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называ­ются элементарными.

Например, функция

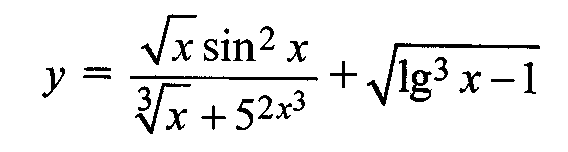
является элементарной, так как здесь число операций сложения, вычитания, умножения, деления и образования сложной функ­ции конечно.

Примерами неэлементарных функций являются функция у = [х] – целая часть х (см. рис. 6.9), функция Дирихле (с. 127).

Классификация функций. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).

Алгебраической называется функция, в которой над аргумен­том проводится конечное число алгебраических действий. К числу алгебраических функций относятся:

• целая рациональная функция (многочлен или полином):

• дробно-рациональная функция – отношение двух многочленов;

• иррациональная функция (если в составе операций над аргу­ментом имеется извлечение корня).

Всякая неалгебраическая функция называется трансцендент­ной. К числу трансцендентных функций относятся функции: по­казательная, логарифмическая, тригонометрические, обратные тригонометрические.

Преобразование графиков. В разделе III «Дифференциальное исчисление» будет показано, как проводить исследование функ­ций и построение их графиков с помощью производной. Вместе с тем актуальными остаются приемы построения графиков функций с помощью преобразования графиков основных эле­ментарных функций.

Пусть задан график функции у =f(x).

Тогда справедливы следующие утверждения.

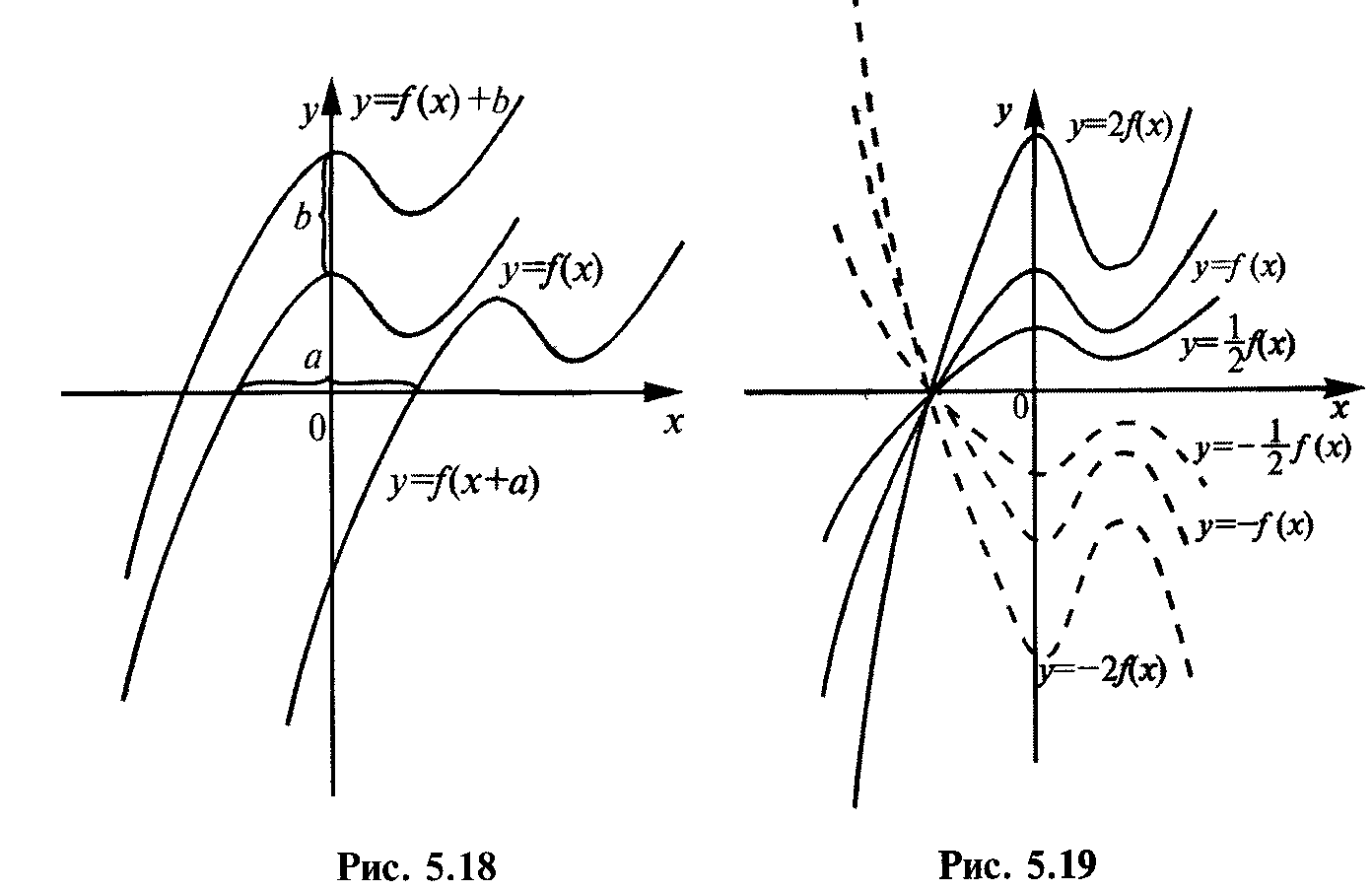
1. График функции у =f(x + а) есть график у = f(х), сдвину­тый (при а > 0 влево, при а < 0 вправо) на a единиц параллель­но оси Ох (рис. 5.18).

2. График функции у =f(x) + b есть график у =f(x), сдвину­тый (при b > 0 вверх, при b < 0 – вниз) на b единиц параллельно оси Оу (см. рис. 5.18).

3. График функции у = mf(x) (т 0) есть график у =f(x), растянутый (при т>1) в т раз или сжатый (при 0 < т < 1) вдоль оси Оу (см. рис. 5.19). При т < 0 график функции у = mf(x) есть зеркальное отображение графика у = –тf(х) от оси Ох.

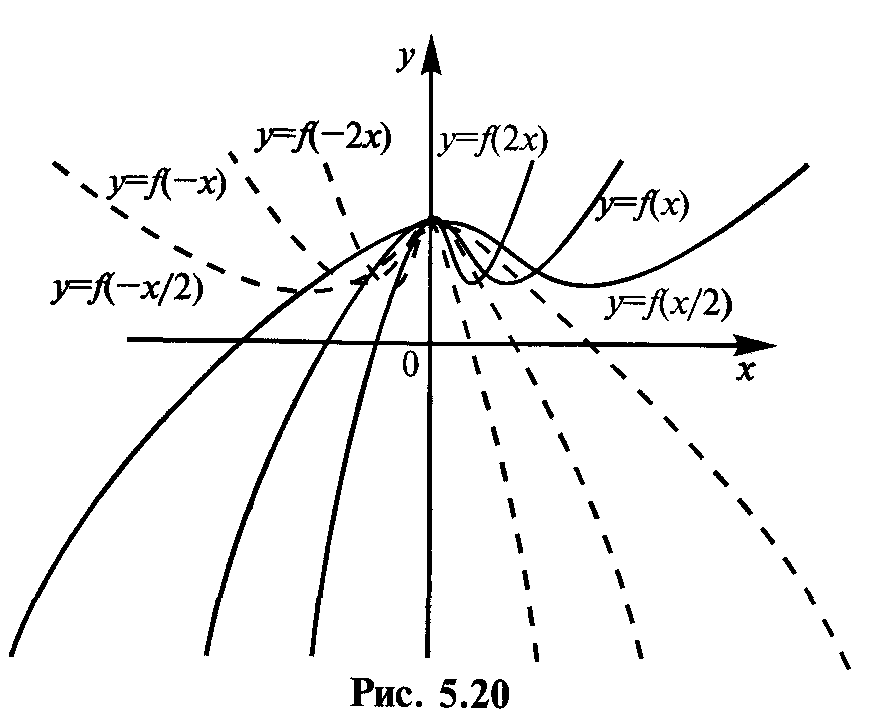
4. График функции у =f(kx) (k  0) есть график у =f(x), сжатый (при k>1) в k раз или растянутый (при 0 < k < 1) вдоль оси Ох (см. рис. 5.20). При -оо < k < 0 график функции у =f(kx) есть зер­кальное отображение графика у =f(–kx) от оси Оу.

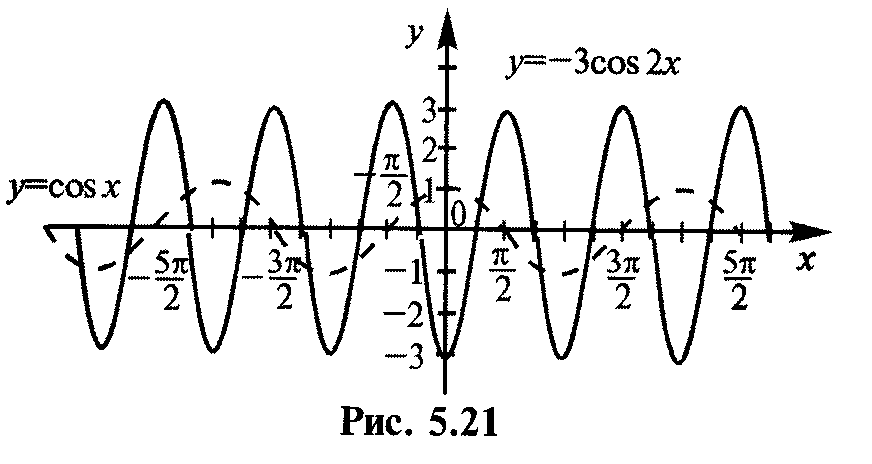
Пример 5.3. По­строить график функ­ции у = –3cos 2х.

Решение. Строим график функ­ции у = –3cos 2х сле­дующим образом (рис. 5.21).

1. Строим график у = cos х.

2. у = cos x -> сжатие графика в 2 раза вдоль оси Ох -> у = = cos 2х.

3. у = cos 2x -> зеркальное отражение графика от оси Ох -> у = –cos 2х.

4. у = -cos 2x-> растяжение графика в 3 раза вдоль оси Оу -> у = –3cos 2х.